Устойчивость систем автоматического управления
Устойчивостью называют свойство системы самостоятельно возвращаться в состояние равновесия после того, как внешнее входное воздействия вывело ее из состояния равновесия. Равновесием называют состояние системы, когда управляемая величина y(t) постоянна, и все ее производные равны нулю. Исследование устойчивости является одной из основных задач в теории автоматического управления.
Как уже отмечалось, процесс управления определяется переходным процессом: законом изменения y(t) после изменения x(t). Переходной процесс САУ можно получить решением дифференциального уравнения САУ (1). Это решение может быть представлено суммой двух составляющих, вынужденной ув(t) и переходной yп(t):
y(t) = ув(t) + yп(t),
где yв(t) определяется свойствами системы и видом входного воздействия. САУ будет устойчивой, если с течением времени переходная составляющая будет стремиться к нулю:
Однозначно судить об устойчивости системы можно по виду ее переходного процесса: затухающий переходной процесс (сходящийся к некоторой постоянной) соответствует устойчивой системе, расходящийся (стремящийся в бесконечность) – неустойчивой.
| ПРИМЕРЫ переходных процессов неустойчивых САУ. | 
|
При исследовании устойчивости САУ решают следующие задачи:
- определение, является ли САУ устойчивой при заданных параметрах;
- определение допустимых изменений параметров САУ без нарушения устойчивости;
|
|
|
- поиск параметров и/или структуры САУ, при которых она может стать устойчивой.
Теорема Ляпунова
Необходимое и достаточное условие устойчивости линейных САУ формулируется в теореме Ляпунова:
- если характеристическое уравнение САУ имеет все корни с отрицательной действительной частью, то система устойчива;
- если хотя бы один корень имеет положительную действительную часть, то САУ неустойчива.
Характеристическое уравнение САУ записывается по виду дифференциального уравнения или передаточной функции системы. Так, из уравнения (1) после преобразования Лапласа мы имеем (см. вывод (2)):
.
Полином в левой части равенства вида:
называется характеристическим. Приравнивание нулю характеристического полинома дает характеристическое уравнение системы или звена:
| (16) |
Уравнение в виде (16) может быть также записано по виду передаточной функции САУ приравниванием знаменателя к нулю:
| (17) |
Корни характеристического уравнения, количество которых соответствует порядку характеристического уравнения САУ, могут быть действительными, комплексными и чисто мнимыми. Их можно представить в виде точек на комплексной плоскости величины р. Согласно теореме, для устойчивости системы необходимо и достаточно, чтобы все корни лежали в левой полуплоскости. Примеродного из возможных распределений в комплексной плоскости корней характеристического уравнения устойчивой САУ 5-ого порядка показан на рис. 75.
|
|
|
| Рис. 75 |
Если хотя бы один из корней окажется справа от мнимой оси, то система будет неустойчивой. Примерывозможных распределений в комплексной плоскости корней характеристического уравнения неустойчивой САУ 5-ого порядка показаны на рис. 76.
| Рис. 76 |
В случае, если среди корней характеристического уравнения имеется нулевой корень или пара сопряженных чисто мнимых корней, расположенных на мнимой оси, система оказывается на границе устойчивости. Примерывозможных распределений в комплексной плоскости корней характеристического уравнения САУ 5-ого порядка, находящейся на границе устойчивости, приведены на рис. 77.
Системы, у которых имеется одна пара мнимых корней, могут совершать незатухающие колебания (автоколебания). Такие системы практически неработоспособны [2, 3, 10, 11].
| Рис. 77 |
Рассмотрим примеры оценки устойчивости по теореме Ляпунова и связь результатов оценки с переходной характеристикой САУ.
|
|
|
Пусть САУ 3-го порядка имеет характеристическое уравнение вида:
.
На рис. 78 показан результат решения этого уравнения, полученный с использованием математического пакета Mathcad. Множество корней уравнения представлено в круглых скобках. Как видно, один из корней уравнения оказался отрицательным действительным числом –3,55, а два других – комплексными сопряженными числами с отрицательной действительной частью –0,525: (–0,525 – 0,657j) и (–0,525 + 0,657j).
| Рис. 78 |
Распределение найденных корней в комплексной плоскости свидетельствует об устойчивости рассматриваемой САУ (см. рис. 78) – корни располагаются в левой полуплоскости комплексной плоскости, что по теореме Ляпунова является достаточным условием устойчивости. Переходная характеристика САУ, полученная с применением специального программного обеспечения моделирования систем по передаточным функциям VisSim, показана на рис. 79. Ее форма подтверждает результат анализа устойчивости по Ляпунову: процесс «сходится» к новому постоянному значению за время, приближенно равное 12 с.
| Рис. 79 |
Аналогично рассмотрим другую САУ 3-го порядка, с характеристическим уравнением вида:
.
|
|
|
На рис. 80 показан результат решения этого уравнения, полученный с использованием математического пакета Mathcad. Множество корней уравнения представлено в круглых скобках. Как видно, один из корней уравнения оказался отрицательным действительным числом –7,2, а два других – комплексными сопряженными числами с положительной действительной частью 1,31: (1,31 + 4,64j) и (1,31 – 4,64j), т.е. распределение корней в комплексной плоскости свидетельствует по теореме Ляпунова о неустойчивости САУ.
| Рис. 80 |
Переходная характеристика рассматриваемой САУ, показанная на рис. 81, подтверждает результат анализа устойчивости по Ляпунову: процесс «расходится», т.е. система не может самостоятельно вернуться к равновесию после того, как ступенчатое воздействие на входе вывело ее из начального состояния равновесия.
| Рис. 81 |
Критерии устойчивости САУ
Для оценки устойчивости необходимо оценить расположение корней характеристического уравнения системы относительно координатных осей комплексной плоскости. Эту оценку можно осуществить непосредственным решением характеристического уравнения. Но для определения устойчивости не обязательно знать значения корней характеристического уравнения, достаточно проверить, являются ли действительные части всех корней отрицательными.
Правила, позволяющие исследовать устойчивость системы без непосредственного нахождения корней характеристического уравнения, называются критериями устойчивости.
На ранней стадии развития теории управления актуальной была задача определения устойчивости полинома без вычисления его корней, т.к. характеристические уравнения высоких порядков трудно было решать «в ручную». Сейчас легко найти корни характеристического полинома с помощью компьютерных программ, однако такой подход не позволяет исследовать устойчивость теоретически, например, определять границы областей устойчивости отдельных параметров САУ.
С помощью критериев устойчивости не только устанавливается факт устойчивости систем, но и оценивается влияние тех или иных параметров и структурных изменений в системе на устойчивость. Математически все формы критериев устойчивости эквивалентны, т.к. они определяют условия, при которых корни характеристического уравнения попадают в левую полуплоскость комплексной системы координат [1, 7, 8].
6.2.1. Критерий Гурвица
Критерий Гурвица относится к алгебраическим критериям устойчивости, которые позволяют установить устойчива ли САУ или нет по результатам алгебраических действий над коэффициентами характеристического уравнения.
Бóльшая часть реальных САУ являются замкнутыми, т.е. имеют общую единичную обратную связь и, соответственно, передаточную функцию вида:
,
где Wраз(р) – передаточная функция разомкнутой САУ (без учета общей обратной связи).
Рассмотрим вывод характеристического уравнения замкнутой САУ, если дана передаточная функция соответствующей ей разомкнутой САУ. Согласно (17) характеристическое уравнение САУ получается приравниванием к нулю знаменателя ее передаточной функции, следовательно, для замкнутой системы запишем:
.
Однако, передаточная функция разомкнутой системы, согласно (2), имеет вид:
следовательно, характеристическое уравнение замкнутой системы может быть записано как:
Дробь равна нулю когда ее числитель равен нулю, следовательно, характеристическое уравнение замкнутой системы можно записать как сумму полиномов числителя и знаменателя передаточной функции разомкнутой системы, прировняв полученное выражение к нулю:
| (18) |
Важно! Для применения критерия Гурвица используется специальная форма записи характеристического уравнения, отличающаяся от (16) обратной нумерацией коэффициентов полинома:
(19)
Критерий Гурвица использует матрицу коэффициентов характеристического уравнения размером n´n, составленную следующим образом:
- по главной диагонали выписываются все коэффициенты характеристического уравнения, начиная с a1 и заканчивая an;
- каждая строка дополняется коэффициентами с возрастающими индексами слева на право так, чтобы чередовались строки с четными и нечетными индексами;
- в случае отсутствия коэффициента, а также, если индекс меньше 0 или больше n, на его месте пишется 0.
В результате получается матрица, первая строка которой содержит коэффициенты уравнения (19) a1, a3, a5,… (все с нечетными номерами) и нулями на месте отсутствующих элементов, вторая строка – коэффициенты a0, a2, a4,… (все с четными номерами) и нулями на месте отсутствующих элементов. Третья строка получается сдвигом первой строки на одну позицию вправо, четвертая – сдвигом второй строки на одну позицию вправо и т.д. Например, для САУ 5-го порядка (n = 5) эта матрица имеет вид:
Критерий Гурвица определяет необходимое и достаточное условие устойчивости САУ следующим образом: все корни характеристического уравнения САУ имеют отрицательные действительные части, если при a0 > 0 все n определителей Гурвица матрицы коэффициентов положительны.
Определители Гурвица вычисляются следующим образом:
и так далее – последний определитель вычисляется для полной матрицы коэффициентов.
При условии положительности всех коэффициентов характеристического уравнения достаточно проверить только n – 1первых определителей Гурвица, не вычисляя определитель для полной матрицы. При этом условии частные случаи критерия Гурвица для систем низких порядков получают, раскрывая определители матрицы коэффициентов. Так, в результате раскрытия определителей, для САУ первого и второго порядков необходимым и достаточным условием устойчивости является собственно положительность всех коэффициентов характеристического уравнения. Для САУ 3-го порядка – положительность всех коэффициентов и условие вида:
| a1×a2 – a0×a3 > 0, | (20) |
для САУ 4-го порядка – положительность всех коэффициентов и условие a3×(a1×a2 – a0×a3) – a4×a12 > 0. Т.о., условия устойчивости сводятся к нескольким неравенствам, что удобно для оценки влияния на устойчивость отдельных параметров звеньев САУ [1, 7, 14].
Рассмотрим систему (рис. 82), в которой регулятор (звено 1) и объект управления (звено 2) задаются передаточными функциями вида:
.
| Рис. 82 |
Определим с помощью критерия Гурвица, при каких значениях коэффициента статического преобразования регулятора k рассматриваемая система будет устойчивой. Запишем передаточную функцию разомкнутой САУ:
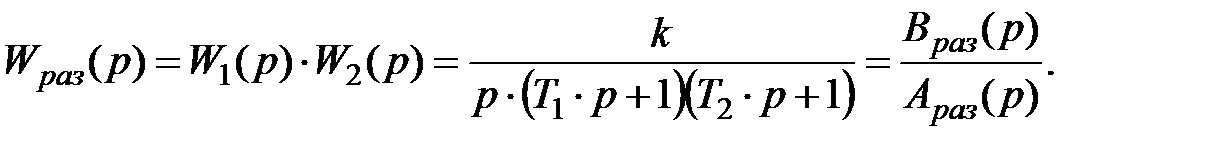
С использованием (18) запишем характеристическое уравнение замкнутой САУ:
Для того уравнения, согласно форме (19), коэффициенты, соответственно равны:
При положительности всех коэффициентов этого уравнения 3-го порядка необходимым условием устойчивости также является выполнение условия (20):
a1×a2 – a0×a3 > 0,
Т.о., рассматриваемая САУ будет устойчива, если значение коэффициента статического преобразования k удовлетворяет условию [7]:
Рассмотрим примеры оценки устойчивости по критерию Гурвица исследованных ранее по теореме Ляпунова систем 3-го порядка (см. рис. 78 и рис. 80). Матрица коэффициентов Гурвица для САУ 3-го порядка имеет общий вид:
,
т.е. матрицы Гурвица для рассматриваемых САУ равны, соответственно:
и 
.
Характеристические уравнения обеих САУ удовлетворяют критерию положительности всех коэффициентов, поэтому для оценки устойчивости по критерию Гурвица достаточно вычислить и проверить на положительность n – 1первых определителей Гурвица, т.е. для 3-го порядка – второй определитель. Результаты вычисления вторых определителей матрицы Гурвица для рассматриваемых систем (см. рис. 78 и рис. 80), полученные с использованием Mathcad, показаны на рис. 83–а и рис. 83–б соответственно. Как видно, результаты оценки устойчивости по Гурвицу совпадают с ранее полученными оценками по Ляпунову и результатами построения переходных характеристик рассматриваемых САУ (см. рис. 79 и рис. 81 соответственно) – положительный определитель соответствует устойчивой САУ, а отрицательный – неустойчивой.
| Рис. 83 |
| а) |
| б) |
6.2.2. Критерий Михайлова
Этот критерий позволяет оценить устойчивость САУ по годографу Михайлова – кривой, представляющая собой геометрическое место концов переменного характеристического вектора САУ. Формула для расчета и построения годографа Михайлова в комплексной плоскости получается подстановкой в характеристический полином САУ комплексной частоты jw вместо р:
| (21) |
Годограф по формуле (21) рассчитывают, изменяя частоту w от 0 до +¥, и строят в комплексной плоскости.
Критерий Михайлова определяет необходимое и достаточное условие устойчивости САУ следующим образом: САУ является устойчивой, если при изменении частоты от 0 до +¥ годограф вектора Михайлова А(jw) начинается на положительной части действительной оси и, не обращаясь в ноль, поворачиваясь против часовой стрелки, проходит последовательно n квадрантов[1] комплексной плоскости, где n – порядок характеристического полинома САУ.
У устойчивых систем годограф Михайлова имеет плавную спиралевидную форму и при w = 0 отсекает на действительной оси в положительном направлении отрезок, равный свободному члену характеристического уравнения а0.
По виду годографа Михайлова можно определить и граничное состояние устойчивости САУ: в случае границы устойчивости первого типа, т.е. наличия у характеристического уравнения САУ нулевого корня (см. рис. 77) отсутствует свободный член характеристического уравнения а0 = 0 и годограф начинается из начала координат. При границе устойчивости второго типа, т.е. наличия у характеристического уравнения САУ пары чисто мнимых корней (см. рис. 77), годограф проходит через начало координат (обращается в ноль) при некотором ненулевом значении w, причем это значение и есть частота незатухающих колебаний системы [1, 2].
Рассмотрим примеры оценки устойчивости по критерию Михайлова исследованных ранее по теореме Ляпунова систем 3-го порядка (см. рис. 78 и рис. 80). Формулы для расчета годографов Михайлова этих систем имеют вид, соответственно:
и
.
Годограф Михайлова для первой САУ показан на рис. 84. Как видно, его форма удовлетворяет всем условиям критерия:
- годограф начинается на положительной части действительной оси (отсекая при w = 0 на действительной оси отрезок, равный свободному члену характеристического уравнения а0 = 3);
- не обращается в ноль;
- с ростом значения частоты w, поворачиваясь против часовой стрелки, проходит последовательно первый, второй квадрант и в третьем квадранте, при w ® ¥, уходит в бесконечность.
| Рис. 84 |
Годограф Михайлова для второй САУ показан на рис. 85. Как видно, его форма не удовлетворяет условиям критерия: годограф с ростом значения частоты w проходит квадранты не последовательно – из первого сразу переходит в четвертый, где при w ® ¥ уходит в бесконечность.
Как видно, результат оценки устойчивости рассматриваемых САУ по Михайлову совпадает с результатами анализа по Ляпунову (см. рис. 78 и рис. 80) и по Гурвицу (см. рис. 83–а и рис. 83–б).
| Рис. 85 |
Следует отметить, что для систем с высоким порядком характеристического уравнения (n = 5 и более) отсчет квадрантов при проверке условий критерия Михайлова после четвертого продолжается против часовой стрелки в том же порядке. Т.е., например, у устойчивой САУ 5-го порядка годограф должен последовательно проходить четыре квадранта, возвращаться в первый (для годографа – по порядку пятый) и в нем уходить в бесконечность. Пример годографа Михайлова для устойчивой САУ 5-го порядка с формулой для расчета годографа вида:
показан на рис. 86. Для удобства анализа начальный участок годографа, полученные при малых значениях частоты w, показан отдельным фрагментом. Видно, что годограф при w = 0 начинается на положительной части действительной оси и, последовательно, против часовой стрелки, проходя пять квадрантов, в пятом уходит в бесконечность.
| Рис. 86 |
6.2.3. Критерий Найквиста для АФХ
Критерии устойчивости Найквиста позволяют оценить устойчивость замкнутой системы по частотным характеристикам соответствующей разомкнутой системы. Напомним, что замкнутой называется САУ с общей единичной отрицательной обратной связью (рис. 87). Передаточная функция замкнутой САУ имеет вид:
,
где Wраз(р) – передаточная функция разомкнутой САУ (без учета общей обратной связи).
| Рис. 87 |
Критерий Найквиста для амплитудно–фазовой характеристики (АФХ) формулируется следующим образом: замкнутая система будет устойчивой, если АФХ соответствующей разомкнутой системы при изменении частоты от 0 до не охватывает точку с координатами [–1, j0].
Рассмотрим произвольную разомкнутую САУ, не содержащую интегрирующих звеньев. В этом случае значение АФХ для частоты w = 0 равно коэффициенту статического преобразования САУ:
W(jw) = W(j0) = k.
При этом, если степень числителя передаточной функции меньше степени знаменателя, то график АФХ, начинаясь в точке с координатами (k, j0) при изменения частоты от 0 до ¥ стремится к началу координат. На рис. 88–а показана АФХ устойчивой САУ – график не охватывает точку с координатами [–1, j0], а на рис. 88–б – неустойчивой (график точку охватывает).
| Рис. 88 |
| а) |
| б) |
Если АФХ разомкнутой САУ проходит через точку с координатами [–1, j0], то соответствующая ей замкнутая САУ находится на границе устойчивости (рис. 89). В этом случае для некоторой частоты w мы имеем А(w) = 1 и j(w) = –180°.
| Рис. 89 |
Если в составе САУ есть интегрирующие звенья, то АФХ при w = 0 обращается в бесконечность, т.е. график АФХ в этом случае начинается не на действительной оси, а приходит из бесконечности. В этом случае для оценки устойчивости по критерию Найквиста в контур включают не только кривую графика АФХ, но и часть окружности бесконечного радиуса, проводимой от действительной оси по часовой стрелке. Пример устойчивой САУ с АФХ такого вида показан на рис. 90–а, неустойчивой – на рис. 90–б [1, 2, 7].
| Рис. 90 |
| а) |
| б) |
Рассмотрим пример оценки устойчивости по критерию Найквиста для АФХ на примере замкнутой САУ, которой соответствует разомкнутая система с передаточной функцией вида:
Запишем по заданной Wраз(p) формулу расчета АФХ:
,
и, изменяя частоту w от 0 до +¥, построим график АФХ разомкнутой САУ с использованием математического пакета Mathcad (рис. 91). Для удобства анализа участок АФХ в области точки [–1, j0], полученный для больших значений частоты w, показан на рис. 91 отдельным фрагментом. По фрагменту хорошо видно, что график охватывает точку [–1, j0], следовательно замкнутая САУ является неустойчивой.
| Рис. 91 |
6.2.4. Критерий Найквиста для ЛАЧХ и ЛФЧХ
Критерий Найквиста для логарифмической амплитудно-частотной и фазочастотной характеристик формулируется следующим образом: замкнутая система устойчива, если для характеристик соответствующей ей разомкнутой системы выполняются два условия:
- при частоте равной частоте среза САУ wс модуль фазочастотной характеристики меньше 180 градусов: 
< 180°;
- при частоте равной wp значение ЛАЧХ меньше нуля: L(wp) < 0.
Как следует из формулировки критерия, для проверки его условий по характеристикам разомкнутой САУ первоначально необходимо определить две частоты: частоту среза wс и частоту wp. После этого для найденных значений частот следует проверить выполнимость обоих условий критерия.
Частотой среза САУ называется частота, при которой ЛАЧХ системы пересекает ось частот, то есть L(wс) = 0. Эта частота также называется частотой единичного усиления САУ, так как сигнал этой частоты на выходе САУ имеет ту же амплитуду, что и на входе: Авых = Авх. Для этого случая справедливо:
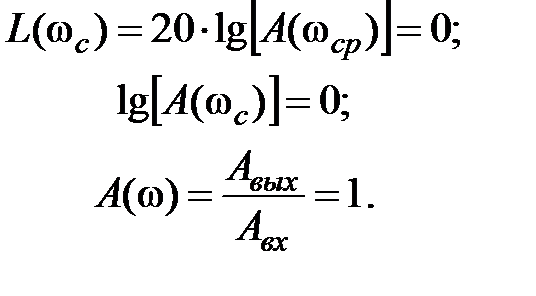
Важно! Не путайте понятия частоты среза отдельных типовых звеньев САУ и всей системы в целом. Определение частот среза типовых звеньев рассмотрено в графе «Примечания» Приложения 1.
Частотой wp САУ называется частота, при которой ФЧХ САУ равняется 180° со знаком «плюс» или со знаком «минус». Если ФЧХ несколько раз пересекает ординату ±180, то выполнение условия проверяется для крайней правой точки.
Важно! Рассматриваемые характеристики – частоты среза wс и частота wp – имеются не у всякой САУ. Если ЛАЧХ системы вообще не пересекает ось частот, то есть L(w) ¹ 0 ни при каких значениях w, то у такой системы нет частоты среза. Аналогично, если ФЧХ системы ни при каких значениях частоты не принимает значение ±180°, то данная САУ не характеризуется параметром wp. В этих случаях для оценки устойчивости следует выбрать другие критерии.
На рис. 92–а показано, как по графикам ЛАЧХ и ЛФЧХ разомкнутой САУ определить частоты wс и wp.
| Рис. 92 |
| а) |
| б) |
| ПРИМЕРЫ: 1) ЛАЧХ САУ без частоты среза wс; 2) ЛФЧХ САУ без частоты wp. |
|
Проверим выполнимость условий критерия Найквиста для характеристик разомкнутой САУ, показанных на рис. 92–а. Определим графически величины L(wp) и j(wс) как показано на рис. 92–б. Как видно, L(wp) < 0, а < 180°, т.е. оба условия критерия Найквиста выполняются, следовательно, замкнутая САУ, соответствующая рассматриваемой разомкнутой, является устойчивой. Из рис. 92–б также можно сделать вывод о том, что для устойчивости САУ по критерию Найквиста достаточно, чтобы выполнялось условие wс < wp.
Для характеристик разомкнутой САУ на рис. 93–а L(wp) > 0, а > 180°, т.е. оба условия критерия Найквиста не выполняются, следовательно, замкнутая САУ, соответствующая рассматриваемой разомкнутой, является неустойчивой. Из рис. 93–а также можно сделать вывод о том, что для неустойчивости САУ по критерию Найквиста достаточно, чтобы выполнялось условие wс > wp.
| Рис. 93 |
| а) |
| б) |
Для характеристик разомкнутой САУ, которой соответствует замкнутая система, находящаяся на границе устойчивости, L(wp) = 0 и = 180°, wс = wp (см. рис. 93–б). У такой системы для сигнала с частотой wс, т.е. с частотой единичного усиления, фазовый сдвиг выходного сигнала относительно входного составляет –180°. Это говорит о том, что после прохождения САУ величина сигнала меняет знак, сохраняя абсолютную величину (энергию), то есть устанавливаются незатухающие колебания. АФХ такой САУ показана на рис. 89 [1, 3, 7, 15].
Рассмотрим пример оценки устойчивости по критерию Найквиста для ЛАЧХ и ЛФЧХ на примере замкнутой САУ, которой соответствует разомкнутая система с передаточной функцией вида:
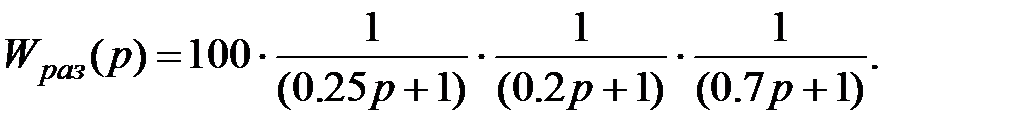
Графики ЛАЧХ и ЛФЧХ разомкнутой САУ, построенные с использованием математического пакета Mathcad по формулам (11) и (12), приведены на рис. 94. Как видно по рисунку, ЛАЧХ равна нулю при wс » 13,5 с-1. ЛФЧХ на частоте wp » 5,7 с-1 меняет знак – после того, как j(w) достигает значения –180° (радиус-вектор, поворачиваясь по часовой стрелки, переходит в верхнюю полуплоскость) отсчет фазового сдвига продолжается в области положительных значений. При этом из двух условий критерия Найквиста формально нарушается только второе: значение ЛАЧХ на частоте среза не является отрицательным (L(wp) » 18 > 0). Первое условие ( < 180°) формально выполняется: » 130° < 180°. Однако следует понимать, что опережение по фазе в 130° соответствует, при отсчете по часовой стрелке без смены знака, отставанию на величину:
j(wс) = –360° + 130° = –230°,
следовательно, замкнутая САУ неустойчива. К такому же выводу можно придти, сравнив величины wс и wp: wс > wp. Оценка устойчивости этой САУ по критерию Найквиста для АФХ, выполненная в конце раздела 6.2.3, также показала отсутствие устойчивости.
Выполним проверку оценки устойчивости по критериям Найквиста с использованием теоремы Ляпунова. По заданной 
запишем с использованием формулы (18) характеристическое уравнение замкнутой САУ:
Решение характеристического уравнения замкнутой САУ, полученное с использованием математического пакета Mathcad, имеет вид:
Множество корней уравнения представлено в круглых скобках. Как видно, один из корней уравнения оказался отрицательным действительным числом –17,74, а два других – комплексными сопряженными числами с положительной действительной частью 3,657. Эти корни равны, соответственно, (3,657+ 12,22j) и (3,657– 12,22j). Т.о. по теореме Ляпунова замкнутая САУ неустойчива, что согласуется с результатами оценки устойчивости, полученными с применением обоих критериев Найквиста.
| Рис. 94 |
Запасы устойчивости САУ
Технические характеристики устройств, входящих в состав САУ, меняются в процессе эксплуатации, и, следовательно, со временем изменяются и постоянные передаточной функции САУ. Следователь, недостаточно спроектировать просто устойчивую систему, нужно, чтобы она сохраняла устойчивость при некоторых изменениях параметров САУ в сравнении с расчетными, т.е. обладала запасами устойчивости. Запас определяет удаление системы от границы устойчивости.
Запасом устойчивости по амплитуде DL называется величина в децибелах, на которую нужно сместить вверх ЛАЧХ разомкнутой САУ так, чтобы привести соответствующую ей устойчивую замкнутую систему к границе устойчивости. На рис. 95 показано смещение вверх ЛАЧХ устойчивой САУ, исходные характеристики которой были рассмотрены в примере оценки устойчивости по критерию Найквиста (см. рис. 92–б).
| Рис. 95 |
Как видно (см. рис. 95), смещение исходной ЛАЧХ параллельно самой себе вверх на величину DL приводит к смещению частоты среза разомкнутой САУ вправо: для новой ЛАЧХ, показанной пунктиром, значение частоты среза wс1 = wp, что, по критерию Найквиста для ЛАЧХ и ЛФЧХ, свидетельствует о нахождении замкнутой системы на границе устойчивости. Из рис. 95 также следует, что величину DL можно определить как:
 ,
| (22) |
где А(wp) < 1 – модуль АФХ на частоте wp.
Зная DL, можно определить величину коэффициента статического преобразования разомкнутой САУ, при которой соответствующая ей замкнутая система окажется на границе устойчивости:
;
;
 ,
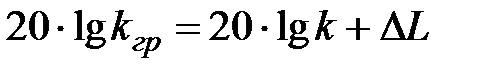| (23) |
где k – коэффициент статического преобразования исходной разомкнутой САУ [2, 7, 14, 15].
Рассмотрим пример определения граничного значения коэффициента статического преобразования для разомкнутой САУ с передаточной функцией вида:
.
ЛАЧХ и ЛФЧХ этой САУ показаны на рис. 96. По графикам характеристик видно, что частота среза САУ составляет wс » 50 с-1, а ЛФЧХ достигает значения –180° на частоте wp » 100 с-1 и после этого меняет знак. Запас устойчивости по амплитуде для этой САУ равен 
, следовательно, по формуле (23):
.
При изменении коэффициента статического преобразования САУ до значения, равного kгр, ЛФЧХ САУ не изменится, а ЛАЧХ сместится вверх (см. рис. 96). Как видно, при найденном значении kгр = 425,975 частота среза разомкнутой САУ wс1 становиться равной 100 с-1, т.е. wс1 = wp. А значит, в соответствии с критерием Найквиста для ЛАЧХ и ЛФЧХ, соответствующая рассматриваемой разомкнутой САУ замкнутая система действительно окажется на границе устойчивости.
| Рис. 96 |
Запас устойчивости по фазе Dj(wс) показывает, насколько должно увеличиться запаздывание по фазе разомкнутой САУ на частоте среза, чтобы замкнутая система оказалась на границе устойчивости (рис. 97).
| Рис. 97 |
На рис. 97 показано смещение вниз ЛФЧХ разомкнутой САУ, исходные характеристики которой были рассмотрены в примере оценки устойчивости по критерию Найквиста (см. рис. 92–б). Как видно, смещение исходной ЛФЧХ параллельно самой себе вниз на величину Dj(wс) приводит к смещению частоты wp разомкнутой САУ влево: для новой ЛФЧХ, показанной пунктиром, значение этой частоты wp1 = wс, что, по критерию Найквиста для ЛАЧХ и ЛФЧХ, свидетельствует о нахождении замкнутой системы на границе устойчивости. Из рис. 97 следует, что величину Dj(wс) можно определить как:
 .
| (24) |
Рекомендуемая величина запаса устойчивости по амплитуде DL для САУ составляет от 10 до 14 дБ, а величина запаса устойчивости по фазе Dj(wс) – от 45° до 60°.
Запасы устойчивости по амплитуде и фазе можно определить и по графику АФХ. На рис. 98 показана АФХ разомкнутой САУ – как видно, график не охватывает точку с координатами [–1, j0], следовательно, замкнутая система устойчива. Определим запас устойчивости по фазе: согласно формуле (23) он равен величине, на которую отличается модуль фазового сдвига для сигнала с частотой wс, от 180°.
| Рис. 98 |
Напомним, что wс это частота единичного усиления: сигнал с такой частотой на выходе САУ имеет ту же величину амплитуды, что и на входе. Следовательно, длина радиус-вектора, проведенного в точку АФХ, которая соответствует wс, равна 1. Эту точку можно найти на графике АФХ по пересечению с окружностью единичного радиуса (см. рис. 98).
Из рис. 98 хорошо видно, что если график АФХ разомкнутой САУ повернуть на величину угла, равную Dj(wс), то график будет проходить через точку [–1, j0], что приведет замкнутую систему к границе устойчивости по критерию Найквиста для АФХ.
Для той же АФХ рассмотрим определение запаса устойчивости по амплитуде. Частоте wp соответствует фазовый сдвиг ±180°, следовательно, точку АФХ, соответствующую этой частоте, можно найти по пересечению графика с действительной осью (рис. 99). Модуль АФХ, определяющий коэффициент ослабления амплитуды сигнала с такой частотой на выходе САУ, равен длине радиус-вектора, проведенного из начала координат в соответствующую точку АФХ. Для АФХ на рис. 99 эта величина равна А(wp), и по ней с использованием формулы (22) можно рассчитать DL.
| Рис. 99 |
Также по виду АФХ можно определить величину коэффициента статического преобразования разомкнутой САУ, при которой соответствующая ей замкнутая система окажется на границе устойчивости. Как видно из рис. 99, А(wp) для устойчивой системы это величина меньше 1, следовательно, для того, чтобы график АФХ проходил через точку [–1, j0], коэффициент статического преобразования САУ нужно умножить на 1/А(wp):
 ,
| (25) |
где k – коэффициент статического преобразования исходной разомкнутой САУ [2, 7, 14, 15].
Рассмотрим пример определения граничного значения коэффициента статического преобразования по АФХ разомкнутой САУ, для которой ранее расчет kгр был выполнен по логарифмическим характеристикам (см. начиная с формулы (23) и до рис. 96). АФХ этой САУ с исходным значением k = 107 показана на рис. 100. Для удобства анализа графика в области точки [–1, j0] его фрагмент показан отдельно. Как видно, у САУ с исходным значением k модуль АФХ А(wp) » 0,25, следовательно, по формуле (25):
Найденное значение kгр = 428 с удовлетворительной точностью совпадает с результатом расчета по ЛАЧХ (kгр = 425,975). Погрешности в расчетах обусловлены приближенным определением по графикам DL и А(wp).
| Рис. 100 |
Как видно из рис. 100, при изменении коэффициента статического преобразования САУ до значения, равного kгр = 428, АФХ САУ пройдет через точку с координатами [–1, j0], а значит, в соответствии с критерием Найквиста для АФХ, соответствующая рассматриваемой разомкнутой САУ замкнутая система действительно окажется на границе устойчивости.
Запасы устойчивости САУ по амплитуде DL и фазе Dj(wс), наряду с показателями, определяемыми по переходной характеристике (см. раздел 2.3.2.), являются основными показателями качества управления.
Литература
1. Анхимюк, В.Л. Теория автоматического управления. / В.Л. Анхимюк, О.Ф. Опейко, Н.Н. Михеев; под ред. В.Л. Анхимюк. – Мн.: Дизайн ПРО, 2000. – 352 с.
2. Бесекерский, В.А. Теория систем автоматического регулирования / В.А. Бесекерский, В.П. Попов. – М.: Наука, 1975. – 766с.
3. Андрющенко, В.А. Теория систем автоматического управления / В.А. Андрющенко. – Л.: ЛГУ, 1990. – 256 с.
4. Клюев, А.С. Проектирование систем автоматизации технологических процессов: справочное пособие / А.С. Клюев, Б.В. Глазов и др. – М.: Энергоатомиздат, 1990. – 464 с.
5. Клюев, А.С. Техника чтения схем автоматического управления и технологического контроля / А.С. Клюев, Б.В. Глазов и др. – М.: Энергоатомиздат, 1991. – 432 с.
6. Федоров, Ю.Н. Справочник инженера по АСУ ТП: проектирование и разработка: учеб.-практ. пособие / Ю.Н. Федоров. – М.: Инфра-Инженерия, 2008. – 928 с.
7. Поляков, К.Ю. Теория автоматического управления для «чайников». К.Ю. Поляков // Преподавание, наука и жизнь [Электронный ресурс]. – 2009. – Режим доступа: http://kpolyakov.narod.ru/uni/teapot.htm. – Дата доступа: 01.06.2011.
8. Тихонов, А.И. Теория автоматического управления: курс лекций / А.И. Тихонов. – Иваново: ИГЭУ, 2002. – 188 с.
9. Яковлев, А.В. Система стабилизации частоты вращения электродвигателя: лабораторная работа по курсу «Технические средства САУ» /А.В. Яковлев. – М.: МГТУ им. Н.Э. Баумана, 2007. – 24 с.
10. Зайцев, Г.Ф. Теория автоматического управления и регулирования / Г.Ф. Зайцев. – К.: Выща шк., 1989. – 431 с.
11. Туманов, М.П. Теория управления. Теория линейных систем автоматического управления: учебное пособие / М.П. Туманов. – М.: МГИЭМ, 2005. – 82 с.
12. Кузьменко, Н.В. Конспект лекций по дисциплине «Автоматизация технологических процессов и производств»: учеб. пособие / Н.В. Кузьменко. – Ангарск: АГТА, 2005. – 77 с.
13. Беспалов, А.В. Динамический звенья. Временные характеристики. Учеб. пособие / А.В. Беспалов, Н.И. Харитонов и др. – М.: РХТУ им. Д.И. Менделеева, 2001. – 80 с.
14. Савин, М.М. Теория автоматического управления: учеб. пособие / М.М. Савин, В.С. Елсуков, О.Н. Пятина. – Ростов на Дону: Феникс, 2007. – 469 с.
15. Филлипс, Ч. Системы управления с обратной связью / Ч. Филлипс, Р. Харбор. – М.: Лаборатория Базовых Знаний, 2001. – 616 с.
Дата добавления: 2018-05-12; просмотров: 1643; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!