Типовые элементарные звенья систем автоматического управления

⇐ ПредыдущаяСтр 3 из 8Следующая ⇒

На первом этапе проектирования САУ решаются задачи синтеза системы на основании данных о назначении системы и конструктивных особенностях объекта управления. При формировании структуры САУ на этом этапе используют функционально необходимые элементы систем, так называемые звенья САУ (датчики величин, преобразователи сигналов, регуляторы, исполнительные устройства и т.д.).

Вторым этапом проектирования САУ является анализ соответствия качественных характеристик проектируемой системы требуемым. Для проведения всех видов анализа САУ, рассмотренных в разделе 3, необходимо иметь ее модель в виде дифференциального уравнения вида (1) или передаточной функции вида (2).

Для получения моделей САУ вводят понятие типового элементарного звена. Под типовым элементарным звеном понимают совокупность элементов САУ, динамические процессы в которых описываются линейным дифференциальным уравнением вида (1) не выше второго порядка (n £ 2). Введение элементарных звеньев дает возможность свести все многообразие технических устройств к небольшому количеству типовых звеньев, что позволяет использовать общие методы анализа для любых САУ. Типы элементарных звеньев САУ приведены в Приложении 1.

Усилительное безынерционное звено

К звеньям этого типа относится любой элемент САУ, у которого в каждый момент времени существует пропорциональная зависимость между выходной величиной y(t) и входным воздействием x(t), т.е. это звено не только в статике, но и в динамике описывается алгебраическим уравнением вида:

y(t) = k× x(t),

где k – коэффициент статического преобразования (коэффициент усиления) звена.

Строго говоря усилительное звено не является динамическим, поскольку изменение y(t) происходит мгновенно, сразу вслед за изменением x(t). Говорят, что дифференциальное уравнение звена имеет нулевой порядок. Передаточная функция звена имеет вид W(p) = k.

При подаче на вход единичной ступеньки x(t) = 1(t) на выходе мгновенно будет получен такой же сигнал, усиленный в k раз (рис. 35).

Рис. 35

Понятно, что ни одно реальное техническое устройство не может мгновенно преобразовывать входное воздействие, однако быстродействие некоторых элементов САУ столь велико (длительность переходного процесса составляет величину менее секунды), что их можно считать звеньями этого типа. Примерами таких элементов является потенциометр, рычаг, электронный усилитель. В первом приближении, без учета явления скручивания и люфта, усилительным безынерционным звеном можно считать редуктор.

В литературе встречаются и другие названия усилительного безынерционного звена: усилитель, идеальное усилительное или пропорциональное звено [1, 2, 10, 13].

Апериодическое звено первого порядка

Звено этого типа (см. Приложение 1) описывается дифференциальным уравнением первого порядка:

где k – коэффициент статического преобразования (коэффициент усиления) звена; Т – некоторая постоянная, имеющая размерность времени (постоянная времени звена).

На рис. 36 показаны переходные характеристики апериодических звеньев первого порядка с k = 10 и разными постоянными времени Т. Видно, что при увеличении Т выходная величина звена y(t) медленнее достигает установившегося значения, равного k, т.е. постоянная времени Т характеризует инерционность звена, и определяет время переходного процесса t_p. В практических расчетах t_p для апериодического звена первого порядки принимают приближенно равным 3×Т.

Рис. 36

Передаточная функция звена имеет вид:

Апериодическими звеньями первого порядка являются такие устройства САУ, как электрические RL- и RC-контуры (используются в качестве корректирующих устройств САУ), электрический генератор постоянного тока (используется в качестве управляющего устройства САУ), датчик температуры – термопара, проточный резервуар с жидкостью или газом (объекты управления в химико-технологических САУ) и многое другое.

Получим модель динамики RC-контура теоретическим способом: запишем уравнения входной и выходной цепей (рис. 37) по закону Кирхгофа:

Рис. 37

Целью моделирования является получение дифференциального уравнения вида (1), связывающего входную – U_вх(t) и выходную – U_вых(t) переменные RC-контура. Для этого нужно в уравнениях входной и выходной цепей избавиться от промежуточной внутренней переменной контура – тока i(t). Продифференцируем уравнение выходной цепи:

и подставим результат выражения i(t) в уравнение входной цепи:

Полученное уравнение соответствует дифференциальному уравнению апериодического звена первого порядка, для которого постоянная времени Т = R×C, т.е. определяется номиналами резистора и конденсатора, используемых в RC-контуре; k = 1; y(t) = U_вых(t); x(t) = U_вх(t).

ПРИМЕР получения модели динамики генератора постоянного тока.

В литературе встречаются и другие названия апериодического звена первого порядка: инерционное звено первого порядка или релаксационное звено [1, 2, 7, 12].

4.3. Апериодическое звено второго порядка и колебательное
устойчивое

Апериодическое звено второго порядка и колебательное устойчивое звено имеют общую форму дифференциального уравнения (см. Приложение 1):

но апериодическим второго порядка звено с таким уравнением называется при условии , а колебательным – при условии .

Общий вид передаточной функции для обоих звеньев:

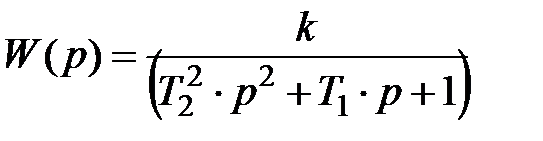Заметим, что при условии уравнение будет иметь положительный дискриминант и, соответственно, действительные корни. Это позволяет разложить знаменатель передаточной функции апериодического звена второго порядка на множители вида:

где .

Если учесть, что при последовательном соединении звеньев их передаточные функции перемножаются, то получается, что апериодическое звено второго порядка эквивалентно двум апериодическим звеньям первого порядка, включенным последовательно друг за другом, с общим коэффициентом статического преобразования k и постоянными времени Т₃ и Т₄.

На рис. 38 показаны переходные характеристики двух апериодических звеньев второго порядка с k = 5 и разными постоянными времени Т₁ и Т₂. Видно, что при увеличении Т₁ и Т₂ выходная величина звена y(t) медленнее достигает установившегося значения, равного k, т.е. постоянные времени и для этого звена определяют время переходного процесса.

Важно! Обратите внимание: несмотря на визуальное сходство переходных характеристик апериодических звеньев первого и второго порядков они имеют принципиальные отличия. Характеристика 2-го порядка имеет точку перегиба: в нулевой момент времени скорость изменения y(t) минимальна, затем она возрастает до точки перегиба, а после нее убывает. Начальный участок переходных характеристик звеньев второго порядка (для t от 0 до 0,5 секунд) показан на рис. 38 в выделенном увеличенном фрагменте. Там же для сравнения приведен аналогичный участок характеристик звеньев первого порядка, показанных на рис. 36. Видно, что для них скорость изменения y(t) максимальна в момент времени t = 0. Далее, за время t_р скорость изменения y(t) убывает до нуля (см. рис. 36).

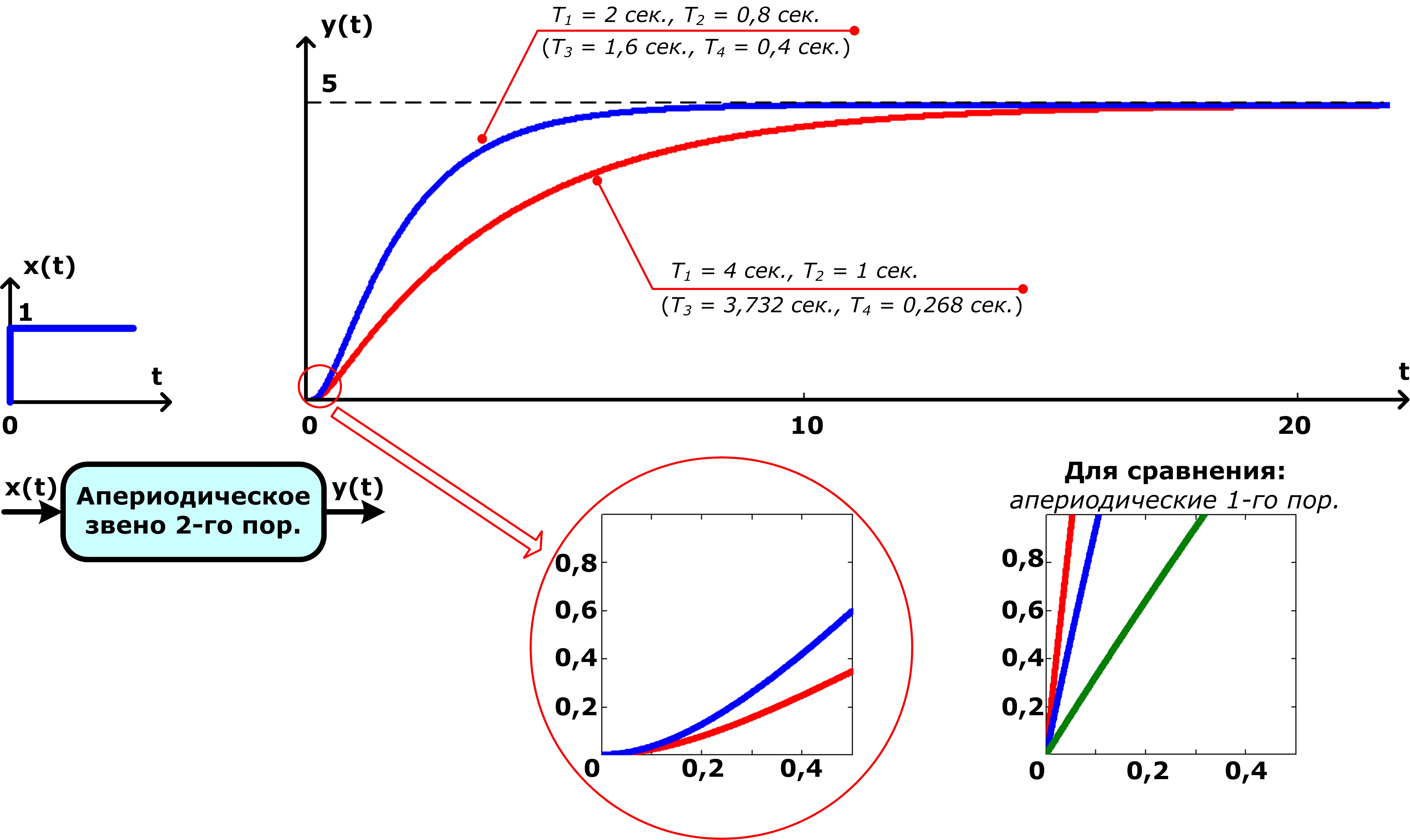
Интервал времени до точки перегиба переходной характеристики апериодического звена второго порядка рассчитывается по формуле:

При условии , т.е. для колебательного устойчивого звена, знаменатель передаточной функции будет иметь отрицательный дискриминант и, соответственно, комплексно-сопряженные корни. Из теории дифференциальных уравнений известно, что свободное движение такой системы содержит гармонические составляющие (синус, косинус), что дает колебания выходной величины при изменении входного сигнала.

Передаточную функцию колебательного звена принято записывать в виде:

где Т – постоянная времени колебательного звена; x – коэффициент затухания (для колебательного устойчивого звена 0 < x < 1). Чем больше x, тем быстрее затухают колебания переходной характеристики звена. При x = 0 получается колебательное гармоническое звено, которое дает незатухающие колебания на выходе (см. Приложение 1). При x ³ 1 имеем апериодическое звено второго порядка.

На рис. 39 показаны переходные характеристики двух колебательных звеньев с одинаковыми значениями коэффициента статического преобразования k = 8 и постоянной времени Т = 1, и разными коэффициентами затухания x. Видно, что колебательность переходной характеристик и перерегулирование у звена с x = 0,25 больше, чем у звена с x = 0,5.

На рис. 40 показаны переходные характеристики двух колебательных звеньев с одинаковыми значениями коэффициента статического преобразования k = 8 и коэффициента затухания x = 0,3, и разными значениями постоянной времени Т. Видно, что время переходного процесса у звена с Т = 2 больше, чем у звена с Т = 1.

Рис. 39

Рис. 40

Колебательными или апериодическими звеньями второго порядка (в зависимости от значений технических характеристик, определяющих соотношение постоянных времени Т₁ и Т₂) являются такие устройства САУ, как электрический RLC-контур; двигатель постоянного тока (см. вывод модели динамики в разделе 2.3.1), упругие механические передачи, например для передачи вращательного движения с упругостью, моментом инерции и коэффициентом скоростного трения, дифманометр (датчик для измерения перепада давления) и другие устройства.

Получим модель динамики RLC-контура теоретическим способом: запишем уравнения входной и выходной цепей (рис. 41) по закону Кирхгофа:

Рис. 41

и подставим результат выражения i(t) в уравнение входной цепи:

Полученное уравнение соответствует дифференциальному уравнению, для которого постоянные времени Т₁ = R×C и , т.е. определяются номиналами резистора, конденсатора и катушки индуктивности, используемых в RLC-контуре; k = 1; y(t) = U_вых(t); x(t) = U_вх(t). Конкретный тип звена – апериодическое второго порядка или колебательное – зависит от соотношения постоянных времени Т₁ и Т₂ ( или соответственно), т.е. в конечном счете определяется номиналами R, L и C. Примеры переходных характеристик RLC-контуров показаны на рис. 42.

Рис. 42

Получим модель динамики механической системы с линейным перемещением, параметрами механических элементов которой являются масса, демпфирование (трение) и упругость (рис. 43). Заметим, что в рассматриваемой системе движение происходит только в одном направлении, перемещение в поперечном направлении не допускается.

Рассмотрим действие внешней силы F(t) на изолированные механические элементы по отдельности. Для массы М по второму закону Ньютона:

где v(t) – скорость; а(t) – ускорение, а s(t) – выходное линейное перемещение (см. рис. 43).

Скорость перемещения поршня демпфера под действием силы F(t) определяется следующим образом:

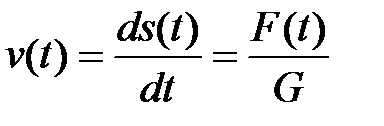где G – коэффициент сопротивления (демпфирования).

Рис. 43

Для упругой пружины в соответствии с законом Гука уравнение движения имеет вид:

где H – коэффициент упругости пружины.

В системе в целом (см. рис. 43) на тело массы М действуют три силы – внешняя сила F(t), сила трения и упругая сила, следовательно, для суммы сил справедливо:

Полученное уравнение динамики имеет второй порядок, однако для приведения к форме стандартного дифференциального уравнения колебательного или апериодического звена второго порядка (см. Приложение 1) постоянный коэффициент слагаемого s(t) в левой части должен быть равен 1. Приведем уравнение динамики к типовому виду, разделив левую и правую часть на коэффициент упругости пружины H:

Полученное уравнение соответствует дифференциальному уравнению, для которого постоянные времени Т₁ = G / H и , т.е. определяются массой, а также величинами G и H; k = 1 / Н; y(t) = s(t); x(t) = F(t).

Т.о., мы показали, что механическая система вида, приведенного на рис. 43, также является колебательным или апериодическим звеном второго порядка. Конкретный тип звена зависит от соотношения постоянных времени Т₁ и Т₂ ( или соответственно), т.е. в конечном счете определяется величинами M, G и H. Рассмотренная механическая система может быть использована, например, в качестве звена модели тормозной системы автомобиля в расчете на одно колесо (кроме рассмотренного звена в такой модели требуется учет массы автомобиля и упругости шины).

Из рассмотренных примеров видно, что, несмотря на различие устройств САУ и их назначения, их математические модели имеют вид одного и того же дифференциального уравнения второго порядка. Рассмотренные типы звеньев в литературе иногда называют инерционными звеньями второго порядка [2, 7, 15].

Интегрирующие звенья

Идеальным интегрирующим звеном называется такое звено, выходная величина которого пропорциональна интегралу по времени от входной величины (см. Приложение 1):

или

где k – коэффициент статического преобразования (коэффициент усиления) идеального интегрирующего звена, равный отношению скорости изменения выходной величины к входной.

Передаточная функция звена имеет вид:

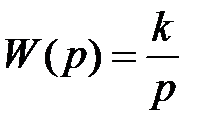Переходная характеристика идеального интегрирующего звена имеет вид наклонной прямой, так как интеграл геометрически представляет собой площадь, ограничиваемую графиком ступенчатого входного воздействия x(t), которая возрастает с течением времени t. Решение дифференциального уравнения идеального интегрирующего звена имеет вид:

откуда для единичной ступеньки (x(t) = 1 при t ³ 0) при нулевых начальных условиях y(0) = 0 получаем линейно возрастающую переходную характеристику y(t) = k×t. На рис. 44 показаны переходные характеристики идеальных интегрирующих звеньев с различными значениями k.

Рис. 44

Простейший бытовой пример идеального интегрирующего звена – ванна, в которую набирается вода. Входное воздействие x(t) для этого объекта это приток (расход) воды через кран, а выходная величина y(t) – уровень воды в ванне. При поступлении воды уровень растет, т.е. система «накапливает» (интегрирует) входной сигнал.

Примерами идеальных интегрирующих звеньев являются такие устройства САУ, как операционный усилитель, используемый в режиме интегрирования (рис. 45–а) и гидравлический демпфер (рис. 45–б).

Уравнение операционного усилителя, используемого в режиме интегрирования, имеет вид:

что соответствует уравнению идеального интегрирующего звена, для которого k = 1/R×C, U_вх = x(t), U_вых = y(t).

Рис. 45

а)

б)

Для гидравлического демпфера входным воздействием является сила F, действующая на поршень, а выходной величиной – перемещение поршня s. Так как скорость движения поршня пропорциональна приложенной силе:

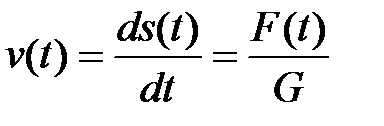где G – коэффициент сопротивления (демпфирования), то перемещение поршня будет пропорционально интегралу от приложенной силы:

Полученное уравнение соответствует уравнению идеального интегрирующего звена, для которого k = 1/G, F(t) = x(t), s(t) = y(t).

Рассмотренная разновидность интегрирующих звеньев называется идеальной, т.к. его уравнение не учитывает инерционность описываемого звеном устройства САУ. В литературе этот тип звена иногда называют астатическим звеном.

Все реальные устройства вносят некоторое замедление в работу, поэтому более точной моделью реальных интегрирующих устройств является интегрирующее звено с замедлением, передаточная функция которого имеет вид:

т.е. представляет собой произведение передаточных функций идеального интегрирующего звена и апериодического звена первого порядка. Т.о., интегрирующее звено с замедлением можно представить последовательным соединением этих двух разновидностей типовых звеньев. Таким звеном может быть описан двигатель, если в качестве выходной величины рассматривать не угловую скорость, а угол поворота, являющийся интегралом от угловой скорости, а также демпфер, если более точно рассматривать его уравнение движения [1, 2, 7].

ПРИМЕР переходной характеристики интегрирующего звена с замедлением.

Дифференцирующие звенья

Идеальное дифференцирующее дает на выходе величину, пропорциональную производной входного сигнала, т.е. скорости изменения входного воздействия (см. Приложение 1):

где k – коэффициент статического преобразования (коэффициент усиления) идеального дифференцирующего звена. Передаточная функция звена имеет вид: .

Дифференцирующее звено реагирует не на изменение самой входной величины, а на изменение ее производной, то есть на тенденцию развития событий. Поэтому говорят, что дифференцирующее звено обладает упреждающим, прогнозирующим действием. С его помощью можно ускорить реакцию САУ на изменяющиеся входные воздействия.

Проанализируем форму переходной характеристики идеального дифференцирующего звена (см. Приложение 1). При подаче на вход звена единичной ступеньки x(t) = 0 для t < 0 и x(t) = 1 для t > 0. Производная постоянной величины равна нулю, следовательно, y(t) = 0 для t < 0 и для t > 0. И только в момент непосредственного изменения входного воздействия с нуля на единицу, т.е. в момент времени t = 0, производная входного сигнала dx(t)/dt не равна нулю:

В результате переходная характеристика идеального дифференцирующего звена в момент времени t = 0 теоретически имеет форму импульса с бесконечно большой амплитудой и бесконечно малой длительностью. Понятно, что такую переходную характеристику невозможно получить с использованием реального устройства САУ. Поэтому идеальное дифференцирующие звено, а также звенья этого типа первого и второго порядков (см. Приложение 1) являются модельными и относятся к физически нереализуемым звеньям.

Приближенно в качестве идеального дифференцирующего звена может рассматриваться операционный усилитель, включенный в режиме дифференцирования (рис. 46–а), и тахогенератор постоянного тока, если в качестве входной величины рассматривать угол поворота его ротора a(t), а в качестве выходной – напряжение якоря U_я(t) (рис. 46–б).

Рис. 46

а)

б)

ПРИМЕР переходной характеристики операционного усилителя в режиме дифференцирования.

В тахогенераторе постоянного тока при неизменном потоке возбуждения напряжение якоря можно считать пропорциональным угловой скорости вращения. В свою очередь скорость вращения есть производная от угла поворота:

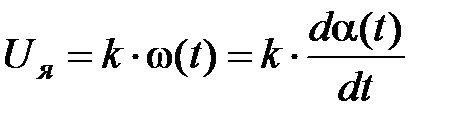что соответствует дифференциальному уравнению идеального дифференцирующего звена с коэффициентом статического преобразования k, y(t) = U_я(t); x(t) = a(t).

Практически дифференцирующие устройства САУ вносят некоторое замедление в работу (обладают инерционностью), поэтому более точной моделью реальных устройств является дифференцирующее звено с замедлением, передаточная функция которого имеет вид:

т.е. представляет собой произведение передаточных функций идеального дифференцирующего звена и апериодического звена первого порядка. Т.о., дифференцирующее звено с замедлением можно представить последовательным соединением этих двух разновидностей типовых звеньев. Примерами дифференцирующего звена с замедлением могут служить трансформатор, емкостной дифференцирующий контур (рис. 47–а) и механическое дифференцирующее устройство, состоящее из пружины и демпфера (рис. 47–б).

Рис. 47

а)

б)

Получим модель динамики емкостного дифференцирующегоконтура (см. рис. 47–а). Запишем уравнения входной и выходной цепей по закону Кирхгофа:

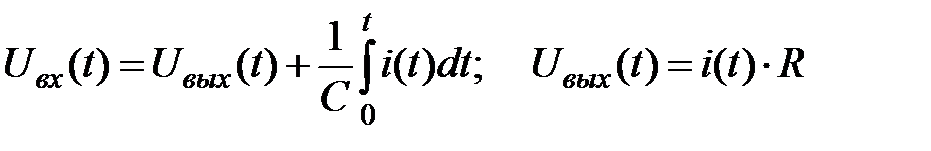Продифференцируем уравнение входной цепи:

и подставим в него ток i(t), выразив его из уравнения выходной цепи:

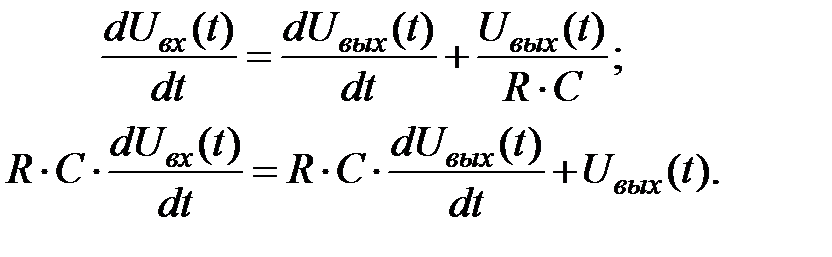
Выведем передаточную функцию емкостного дифференцирующегоконтура:

Полученная W(p) соответствует передаточной функции дифференцирующего звена с замедлением, у которого k = T = R×C.

Получим модель динамики механического дифференцирующего устройства (см. рис. 47–б) для y(t) = s_вых(t); x(t) = s_вх(t) в предположении, что элемент трения (демпфер) и упругости (пружина) имеют нулевую массу. Уравнение движение демпфера для данного случая имеет вид:

где G – коэффициент сопротивления (демпфирования). Для пружины с коэффициентом упругости H уравнение движения имеет вид:

следовательно, после подстановки:

Выведем передаточную функцию механического дифференцирующего устройства:

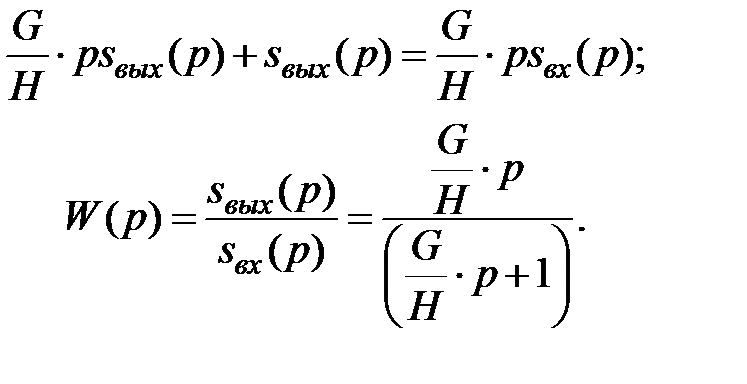
Полученная W(p) соответствует передаточной функции дифференцирующего звена с замедлением, у которого k = T = G/H [1, 2, 7, 15].

ПРИМЕР переходной характеристики дифференцирующего звена с замедлением.

Дата добавления: 2018-05-12; просмотров: 3096; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 234 5 6 7 8 Следующая ⇒

Мы поможем в написании ваших работ!