Теорема о разложении многочлена на линейные множители
Всякий многочлен n – ой степени разлагается на n линейных множителей вида х – а и множитель, равный коэффициенту при старшей степени xn.
Доказательство. Пусть f (x) = A0xn + A1xn - 1 + … + An — многочлен n – ой степени. Этот многочлен в силу основной теоремы алгебры имеет один корень а1. Тогда из следствия теоремы Безу будем иметь f (x) = (х – а1)·f1 (x), где f1 (x) — многочлен степени n - 1. Многочлен f1 (x) тоже имеет корень а2.
Тогда f1 (x) = (х – а2 )·f2 (x), где f 2 (x) — многочлен степени n – 2. Аналогично f2 (x) = (х – а3)·f3 (x). Продолжая процесс выделения линейных множителей, дойдём до соотношения fn(x) = (х – а n )·fn, где fn — число (многочлен нулевой степени), и это число равно коэффициенту при хn, то есть fn = А0. На основании всех этих равенств можно записать
f (x) = А0·( х – а 1)·( х – а2)· … ·( х – аn)
Разложение дроби на простейшие.
Для начала разберем теорию, далее решим парочку примеров для закрепления материала по разложению дробно рациональной функции на сумму простейших дробей. Подробно остановимся на методе неопределенных коэффициентов и методе частных значений, а также на их комбинации.
Простейшие дроби часто называют элементарыми дробями.
Различают следующие виды простейших дробей:
1. 
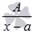
2. 
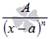
3. 
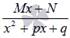
4. 
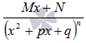
где A, M, N, a, p, q – числа, а дискриминант знаменателя в дробях 3) и 4) меньше нуля.
Называют их соответственно дробями первого, второго, третьего и четвертого типов.
Для чего вообще дробь раскладывать на простейшие?
|
|
|
Приведем математическую аналогию. Часто приходится заниматься упрощением вида выражения, чтобы можно было проводить какие-то действия с ним. Так вот, представление дробно рациональной функции в виде суммы простейших дробей примерно то же самое. Применяется для разложения функций в степенные ряды, ряды Лорана и, конечно же, для нахождения интегралов.
К примеру, требуетя взять интеграл от дробно рациональной функции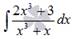 
. После разложения подынтегральной функции на простейшие дроби, все сводится к достаточно простым интегралам
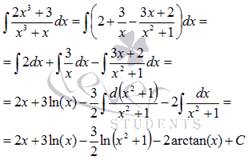
Но об интегралах в другом разделе.
Пример.
Разложить дробь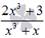 
на простейшие.
Решение.
Вообще отношение многочленов раскладывают на простейшие дроби, если степень многочлена числителя меньше степени многочлена в знаменателе. В противном случае сначала проводят деление многочлена числителя на многочлен знаменателя, а уже затем проводят разложение правильной дробно рациональной функции.
Выполним деление столбиком (уголком):
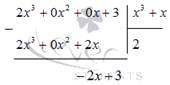
Следовательно, исходная дробь примет вид:
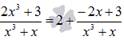
Таким образом, на простейшие дроби будем раскладывать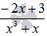 
Интегрирование рациональных дробей
Рациональной дробью называется дробь P(x)/Q(x), числитель P(x) и знаменатель Q(x) которой – многочлены. Рациональные дроби бывают неправильные, если степень многочлена в её числителе не меньше степени многочлена в знаменателе, и правильные, если степень многочлена в числителе меньше степени многочлена в знаменателе.
|
|
|
У любой неправильной дроби можно выделить её целую часть. Для этого следует по правилу деления многочленов разделить числитель на знаменатель. Поэтому любую неправильную дробь можно представить в виде суммы её целой части и некоторой правильной дроби.
Например, неправильную дробь
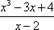
можно представить в виде
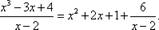
Таким образом, если необходимо проинтегрировать неправильную дробь, то, представив её в виде суммы многочлена и правильной дроби, с помощью метода разложения сведём решение к интегрированию правильной дроби.
Ограничимся интегрированием лишь правильных рациональных дробей, знаменателями которых являются многочлены первой и второй степени. В общем виде интегралы от таких дробей записываются следующим образом:
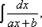
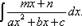
При интегрировании дробей можно использовать следующую формулу, получаемую с помощью метода замены переменной:
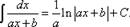
Остроградского метод
Остроградского метод, метод выделения рациональной части неопределённого интеграла
|
|
|
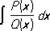
где Q (x) — многочлен степени п, имеющий кратные корни, а Р (х)— многочлен степени m £ n — 1.
О. м. позволяет алгебраическим путём представить такой интеграл в виде суммы двух слагаемых, из которых первое является рациональной функцией переменного х, а второе рациональной части не содержит. Имеет место равенство
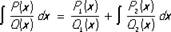
где Q1, Q2, P1, P2— многочлены степеней соответственно n1, n2, m1, m2, причём n1 + n2= n, m1 £ n1 — 1, m2 £ n2 — 1 и многочлен Q2(x) не имеет кратных корней. Многочлен Q1(x) является наибольшим общим делителем многочленов Q (x) и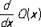 
, и, следовательно, явное выражение Q1(x) можно найти, например, с помощью Евклида алгоритма. Дифференцируя правую и левую части (1), получим тождество
.
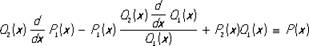Тождество (2) позволяет найти явное выражение многочленов P1(x) и P2(x) неопределённых коэффициентов методом.
О. м. был впервые предложен в 1844 М. В. Остроградским.
Дата добавления: 2018-05-12; просмотров: 885; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!