Вычисление объема тела по площадям его параллельных сечений

Рассмотрим тело D, ограниченное плоскостями х = а и х = b (рис. 247).

Через S(x) обозначим площадь сечения тела D плоскостью, проходящей через точку с абсциссой х [а; b] и перпендикулярной оси Ох. Будем предполагать, что

1) функция S(x) непрерывна на [а; b];

2) для любых x1 и x2 из [а; b] сечения тела D плоскостями х = x1 и х = x1 таковы, что одно из них проектируется в другое.

Тело D, обладающее этими свойствами, будем называть телом с допустимыми параллельными сечениями.

Теорема. Объем тела с допустимыми параллельными сечениями вычисляется по формуле

Отрезок [а; b] точками

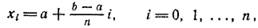
разобьем на п отрезков [хi—1 ; хi] длины

Пусть тi и Mi — наименьшее и наибольшее значения функции S(x) на отрезке

[хi—1 ; хi] .

Плоскостями х = хi, где i = 1, 2, ..., п — 1, тело D разобьем на n слоев. Выделим i-й слой, соответствующий отрезку [хi—1 ; хi], и построим два цилиндра высрты Δ хi :

один с основанием площади Mi , содержащий i-й слой, а другой с основанием площади тi , содержащийся в i-м слое (рис. 248).

Объемы этих цилиндров равны Mi Δ хi и тi Δ хi.

Произведя указанные построения для каждого слоя, получим два ступенчатых тела D'n и D"n таких, что D'n < D < D''n.

Их объемы равны

Так как функция S(x) непрерывна, то V'n и V"n при п —> ∞ имеют один и тот же предел, равный .

Следовательно, объем тела D вычисляется по формуле (1).

Замечание. Можно доказать, что формула (1) остается справедливой и в том случае, когда условие 2) для тела D не выполняется.

Задача. Определить объем тела, отсекаемого от прямого кругового цилиндра плоскостью, проходящей через диаметр основания и составляющей с плоскостью основания угол α (α < 90°). Радиус основания цилиндра равен R.

Введем систему координат так, как показано на рис. 249, и рассмотрим сечения данного тела плоскостями, перпендикулярными оси Оx.

Вычислим площадь сечения плоскостью, проходящей через точку А с абсциссой х,

|х| < R. Это сечение представляет собой прямоугольный треугольник ABC, и поэтому

Объем тела вращения.

Пусть тело образовано вращением вокруг оси OX криволинейной трапеции, ограниченной непрерывной на отрезке [a; b] функцией f (x). Его объем выражается формулой

Пусть тело заключено между плоскостями x = a и x = b, а площадь его сечения плоскостью, проходящей через точку x, – непрерывная на отрезке [a; b] функция σ (x). Тогда его объем равен

Геометрическое и механическое приложения определенного интеграла

Если на отрезке [a,b] задана функция f(x)≥0, то, как известно из определения определенного интеграла, он определяет площадь криволинейной трапеции, ограниченной линиями y=f(x), осью ОХ и прямыми x=a, x=b; т.е.

Если же функция f(x)≤0 на интервале [a, b], то и определенный интеграл также ≤0. Но по абсолютной величине определенный интеграл равен площади S соответствующей криволинейной трапеции

Если функция y=f(x) конечное число раз меняет знак на отрезке [a,b], то интеграл по всему отрезку [a,b] разбиваем по частичным отрезкам.

Интеграл будет положителен на тех отрезках, где f(x) , и отрицателен там где f(x) . Таким образом, интеграл по всему отрезку даст разность площадей, лежащих выше и ниже оси ОХ.

Для того, чтобы получить сумму площадей в обычном смысле, нужно найти сумму абсолютных величин интегралов по указанным выше отрезкам и вычислить интеграл.

Пример 1.

Вычислить площадь S, ограниченную синусоидой y=sinx и осью ОХ, при 0 .

Решение:

т.к. sinx , при 0 и sinx при , то имеем

Следовательно, кв.ед.

Если нужно вычислить площадь, ограниченную кривыми y=f1(x) и y=f2(x) и ординатами x=a и х=b, при условии, что f1(x) f2(x) будем, очевидно, иметь.

(Числовые ряды)

1.Числовой ряд —это числовая последовательность, рассматриваемая вместе с другой последовательностью, которая называется последовательностью частичных сумм (ряда).

Рассматриваются числовые ряды двух видов

вещественные числовые ряды — изучаются в математическом анализе;

комплексные числовые ряды — изучаются в комплексном анализе;

Важнейший вопрос исследования числовых рядов — это сходимость числовых рядов.

Числовые ряды применяются в качестве системы приближений к числам.

1.1Сумма числового ряда определяется как предел, к которому стремятся суммы первых n слагаемых ряда, когда n неограниченно растёт. Если такой предел существует и конечен, то говорят, что ряд сходится, в противном случае — что он расходится[1]. Элементы ряда представляют собой либо вещественные, либо комплексные числа.

Свойства сходящихся рядов.

1. Члены сходящегося ряда можно умножить на одно и то же число k. Полученный ряд будет сходиться, а сумма его будет в k раз больше суммы исходного ряда.

Доказательство. Для второго ряда частичная сумма будет равна . По теореме о предельном переходе в равенстве 2. Члены сходящегося ряда можно группировать. Полученный ряд будет сходиться, и сумма его не изменится.

Сгруппируем члены ряда, например, так. Видно, что частичные суммы группированного ряда представляют собой подпоследовательность последовательности частичных сумм исходного ряда. Так как последовательность сходится, то и подпоследовательность сходится к тому же пределу.

3.В сходящемся ряде можно отбросить конечное число первых членов . Полученный ряд будет сходиться, а его сумма будет меньше суммы исходного ряда на B.

Запишем частичные суммы второго ряда . По теореме о предельном переходе в равенстве .

Замечание. Ряд, полученный из исходного ряда отбрасыванием первых k членов, называется остатком ряда и обозначается

4. Для того чтобы ряд сходился необходимо и достаточно, чтобы сходился остаток ряда. (Докажите это самостоятельно, используя доказательство свойства 3).

Поэтому сходимость ряда можно исследовать, «начиная с некоторого n».

5. Сходящиеся ряды можно складывать (или вычитать), получая сходящийся ряд с суммой, равной сумме (или разности) сумм исходных рядов.

Рассмотрим два сходящихся ряда и . Рассмотрим ряд , где . . Переходя к пределу в равенстве, получим.

Примеры.

1. Ряд —58+100+1+0,5+0,25+0,125+… сходится. В самом деле, отбросив первых четыре члена ряда (свойства 3,4), получим сходящуюся бесконечно убывающую геометрическую прогрессию

2. Ряд расходится. Он представляет собой сумму двух рядов: сходящейся геометрической прогрессии (нечетные члены) и гармонического ряда (четные члены). Если бы этот ряд сходился, то, вычитая из него почленно сходящийся ряд , мы должны были бы по свойству 5 получить сходящийся ряд. А получаем расходящийся гармонический ряд. Следовательно, исходный ряд расходится.

3. Ряд сходится. Рассмотрим сходящийся ряд . Группируем его члены , получаем исходный ряд. Следовательно, он сходится (свойство 2), и его сумма равна 1.

3. –

4.Критерий сходимости положительных рядов (критерий Коши) —основной признак сходимости числовых рядов, установленный Огюстеном Коши.

Положительный ряд сходится тогда и только тогда, когда последовательность его частичных сумм ограничена сверху.

Доказательство

Необходимое условие

Так как ряд сходится, то последовательность частичных сумм имеет предел. Следовательно она ограничена. А значит она ограничена и снизу и сверху. Доказано

Достаточное условие

Дан положительный ряд и последовательность частичных сумм ограничена сверху. Покажем, что наша последовательность(из членов ряда) неубывающая: Теперь используем свойство из теоремы о монотонной последовательности и получим, что последовательность частичных сумм сходится (она монотонно не убывает и ограничена сверху), следовательно ряд сходится (по определению).

Уравнение:

Для сходимости ряда необходимо и достаточно, чтобы все отрезки этого ряда с достаточно большими номерами были сколь угодно малы. Другими словами, ряд сходится тогда и только тогда, когда

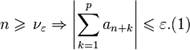
5. –

6.Первый признак сравнения.Пусть даны два ряда с положительными членами

(17)

(18)

и каждый член ряда (17) не превосходит соответствующего члена ряда (18), т.е. выполняется (n = 1, 2, 3, …). Тогда, если сходится ряд (18), то сходится и ряд (17). Если ряд (17) расходится, то ряд (18) также расходится. Этот признак остается в силе, если условие выполняется не для всех n, а лишь начиная с некоторого номера n = N.

7. Второй признак сравнения.Если существует конечный отличный от нуля предел

то оба ряда с положительными членами

одновременно сходятся или одновременно расходятся.

При использовании этих признаков исследуемый ряд часто сравнивается или с бесконечной геометрической прогрессией

, q > 0, (19)

которая при q < 1 сходится и имеет сумму S = a / (1-q), а при q 1 расходится, или с расходящимся гармоническим рядом

. (20)

8. Признак Даламбера. Если для ряда

(11)

существует предел

, (12)

то ряд (11) сходится, если D<1 и расходится, если D>1.

9. Признак Коши. Если для ряда

(13)

существует предел

, (14)

то ряд (13) сходится, если c<1, и расходится, если c>1.

10.Интегральный признак Маклорена – Коши. Этот признак построен на идее сравнения ряда с несобственным интегралом. Представим ряд с положительными членами в виде

, (15)

где f (n) = un - значение некоторой функции f(x) при x = n, определенной в области x 1.

Если f(x) при x 1 непрерывная, положительная и монотонно убывающая функция, то ряд (15) сходится или расходится в зависимости от того, сходится или расходится интеграл

т.е. существует конечный предел

. (16)

11.Теорема Лейбница (признак Лейбница) — теорема об условной сходимости знакочередующихся рядов, сформулированная немецким математиком Лейбницем.

Формулировка

Теорема формулируется следующим образом. Знакочередующийся ряд

сходится, если выполняются оба условия:

Дата добавления: 2018-05-12; просмотров: 457; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 5 6 7 8 9 101112 13 14 Следующая ⇒

Мы поможем в написании ваших работ!