Наибольшее и наименьшее значения функции двух переменных в замкнутой области
Теорема 1.5 Пусть в замкнутой области D задана функция z=z(x,y), имеющая непрерывные частные производные первого порядка. Граница Г области D является кусочно гладкой (т. е. состоит из кусков "гладких на ощупь" кривых или прямых). Тогда в области Dфункция z(x,y) достигает своего наибольшего M и наименьшего m значений.
Без доказательства.
Можно предложить следующий план нахождения M и m.
1. Строим чертёж, выделяем все части границы области D и находим все "угловые" точки границы.
2. Находим стационарные точки внутри D.
3. Находим стационарные точки на каждой из границ.
4. Вычисляем во всех стационарных и угловых точках, а затем выбираем наибольшее M и наименьшее m значения.
Пример 1.14 Найти наибольшее M и наименьшее m значения функции z = 4x2-2xy+y2-8x в замкнутой области D, ограниченной: x = 0, y = 0, 4x+3y=12 .
Решение
1. Построим область D (рис. 1.5) на плоскости Оху.
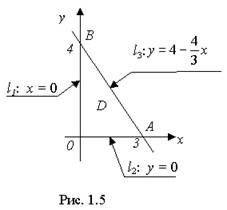
Угловые точки: О (0; 0), В (0; 4), А (3; 0).
Граница Г области D состоит из трёх частей:
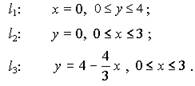
2. Найдём стационарные точки внутри области D:
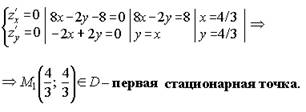
3. Стационарные точки на границах l1, l2, l3:
Достаточные условия экстремума функции двух переменных
Пусть в некоторой области, содержащей точку М0(х0, у0), функция f (x, y) имеет непрерывные частные производные до второго порядка в точке М0(х0, у0) и некоторой её окрестности. Пусть, кроме того, пусть в этой точке М0(х0, у0) выполняются необходимые условия экстремума функции f (x, y)
|
|
|
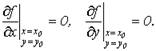(1)
Тогда функция f (x, y) в точке М0(х0, у0) имеет максимум, если
В2– А·С < 0, A < 0;
функция f (x, y) в точке М0(х0, у0) имеет минимум, если
В2– А·С < 0, A > 0;
функция f (x, y) в точке М0(х0, у0) не имеет ни максимума, ни минимума, если
В2– А·С > 0;
функция f (x, y) в точке М0(х0, у0) может иметь, и может не иметь экстремум (в этом случае требуются дополнительные исследования), если
В2– А·С = 0;
где
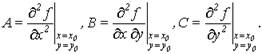
Доказательство. Представим приращение функции по формуле Тейлора в виде
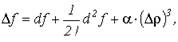(2)
где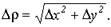 
Так как для функции f (x, y) в точке М0(х0, у0) выполнены соотношения (1), то (2) можно представить в виде
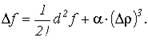(3)
Для достаточно малого Δρ знак левой части соотношения (3) будет совпадать с d2 f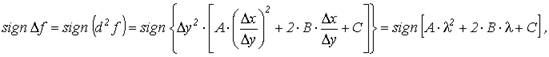 
где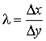 
, Δу ≠ 0 и обозначение sign A означает знак величины А
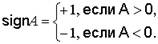
Знакоопределённость квадратного трёхчлена, а значит определённость знака приращения функции для любых значений λ, имеет место только в одном случае - в случае отрицательного дискриминанта квадратного трехчлена В2 – А С < 0. Если к тому же А < 0, то квадратный трехчлен отрицателен для любых значений λ, значит отрицательно приращение функции, что соответствует случаю локального максимума функции в данной точке.
Лагранжа метод множителей
метод решения задач на Условный экстремум; Л. м. м. заключается в сведении этих задач к задачам на безусловный экстремум вспомогательной функции — т. н. функции Лагранжа.
|
|
|
Для задачи об экстремуме функции f (х1, x2,..., xn) при условиях (уравнениях связи) φi(x1, x2, ..., xn) = 0, i = 1, 2,..., m, функция Лагранжа имеет вид
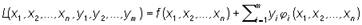
Множители y1, y2, ..., ym наз. множителями Лагранжа.
Если величины x1, x2, ..., xn, y1, y2, ..., ym суть решения уравнений, определяющих стационарные точки функции Лагранжа, а именно, для дифференцируемых функций являются решениями системы уравнений
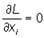i = 1, …, n; 
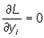i = 1, …,m,
то при достаточно общих предположениях x1, x2, ..., xn доставляют экстремум функции f. Функция Лагранжа L применяется также при исследовании задач вариационного исчисления и математического программирования. Впервые Л. м. м. был предложен в 1797 Ж. Лагранжем в связи с задачами дифференциального исчисления.
(ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ)
Дата добавления: 2018-05-12; просмотров: 1264; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!