Первообразная и неопределенный интеграл
Основной задачей дифференциального исчисления является нахождение производной f '(x) или дифференциала f '(x)dx данной функции f(x)
В интегральном исчислении решается обратная задача:
Дана функция f(x); требуется найти такую функцию F(x), производная которой равна f(x) или дифференциал которой равен f(x)dx в области определения функции f(x), т.е. в этой области функции f(x) и F(x) связаны соотношением
F'(x)=f(x)
или
dF(x)= F'(x)dx= f(x)dx
Определение 1: Функция F(x) называется первообразной функцией для данной функции f(x), если для любого x из области определения f(x) выполняется равенство F'(x)= f(x) или dF(x)= f(x)dx
Из дифференциального исчисления известно что если две функции f(x) и j(x) отличаются друг от друга на постоянную величину, то производные или дифференциалы этих функций равны, т.е. если
f(x) = j(x) + C
то
f '(x) = j'(x)
или
f '(x)dx = j'(x)dx
Известно также, что, и наоборот, если две функции f(x) и j(x) имеют одну и ту же производную или один и тот-же дифференциал, то они отличаются друг от друга на постоянную величину, т.е. если
f '(x) = j'(x) или df(x) = dj(x),
то
f(x) = j(x) + С
Отсюда непосредственно следует, что если в формуле y = F(x) + C мы будем придавать постоянной C все возможные значения, то получим все возможные первообразные функции для функции f (x)
Определение 2: Множество F(x) + C всех первообразных функций для данной функции f (x) , где C принимает все возможные числовые значения, называется неопределенным интегралом от функции f (x) и обозначается символом
|
|
|
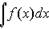
Таким образом, по определению,
где F'(x) = f (x) или dF(x) = f(x)dx и С - произвольная постоянная. В последней формуле f(x) называется подинтегральной функцией, f(x)dx - подинтегральным выражением, а символ 
- знаком неопределенного интеграла.
Неопределенным интегралом называют не только множество всех первообразных, но и любую функцию этого множества.
Таким образом, неопределенный интеграл представляет собой любую функцию, дифференциал которой равен подинтегральному выражению, а производная равна подинтегральной функции
Нахождение первообразной по данной функции f(x) называется интегрированием и является действием, обратным дифференцированию.
Таблица простейших интегралов
2. –
Метод подведения под знак дифференциала
Метод подведения под знак дифференциала основан на равенстве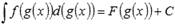 
. То есть, главной задачей является приведение подынтегральной функции к виду 
. Поэтому желательно иметь перед глазами таблицу производных основных элементарных функций. Перепишем ее в виде дифференциалов
и таблицу первообразных.
Пример.
Найти неопределенный интеграл 
.
Решение.
Подынтегральное выражение уже является подведенным под знак дифференциала.
|
|
|
Так как 
(по таблице первообразных), то 
.
Метод замены переменной
Рассмотрим неопределенный интеграл F(x) некоторой функции f(x). Для упрощения вычисления интеграла часто удобно выполнить замену переменной. Переход от x к новой переменной u описывается выражением
где x = g (u) - подстановка. Соответственно, обратная функция u = g −1(x) описывает зависимость новой переменной от старой.
Важно иметь ввиду, что дифференциал dx должен быть заменен на дифференциал новой переменной du.
Для определенного интеграла, кроме этого, необходимо также изменить пределы интегрирования. Смотрите об этом подробнее на странице "Определенный интеграл. Формула Ньютона-Лейбница".
Пример 1
Вычислить 
.
Решение.
Сделаем замену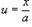 
. Тогда 
. Следовательно, интеграл принимает вид
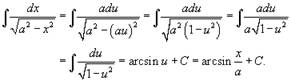
Интегрирование по частям
Пусть u(x) и v(x) являются дифференцируемыми функциями. Дифференциал произведения функций u и v определяется формулой
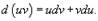
Проинтегрировав обе части этого выражения, получим
или, переставляя члены,
Это и есть формула интегрирования по частям.
Пример 1
Вычислить интеграл 
.
Решение.
Используем формулу интегрирования по частям 
. Пусть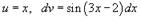 
. Тогда
|
|
|
Следовательно,
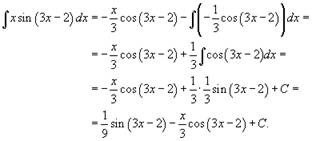
Теорема Безу
При делении многочлена f (x) = A0xn + A1xn-1 + … + An на разность х – а получается остаток, равный f (а).
Доказательство. При делении f (x) на х – а частным будет многочлен f1(x), степень которого будет на единицу ниже степени многочлена f (x) и остаток, который будет постоянным числом: f (x) = (х – а )·f1(x) + R. Переходя к пределу в левой и правой части этого равенства при х → а, получим R = f(а).
Если х = а — корень многочлена, то f (а) = 0 и многочлен f (x) нацело делится на разность х – а и многочлен представляется в виде
f (x) = ( х – а )·f1 (x),
где f1 (x) — многочлен.
Дата добавления: 2018-05-12; просмотров: 658; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!