Инвариантность формы полного дифференциала
Выражение полного дифференциала функции нескольких переменных имеет тот же вид вне зависимости от того, являются ли u и v независимыми переменными или функциями других независимых переменных.
Доказательство опирается на формулу полного дифференциала
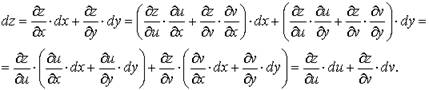
Что и требовалось доказать.
5.Полная производная функции— производная функции по времени вдоль траектории. Пусть функция имеет вид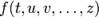 
и ее аргументы зависят от времени: 
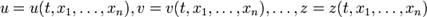. Тогда 
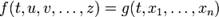, где 
— параметры задающие траекторию. Полная производная функции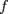 
(в точке 
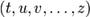) в таком случае равна частной производной по времени (в соответствующей точке 
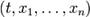) и может быть вычислена по формуле:
,
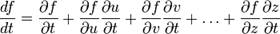где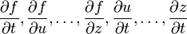 
— частные производные. Следует отметить, что обозначение 
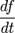является условным и не имеет отношения к делению дифференциалов. Кроме того, полная производная функции зависит не только от самой функции, но и от траектории.
Например, полная производная функции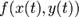 
:
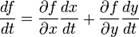
Здесь нет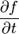 
так как 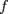сама по себе («явно») не зависит от 
.
Полный дифференциал
Перевод
Полный дифференциал
функции f (x, у, z,...) нескольких независимых переменных — выражение
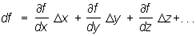
в случае, когда оно отличается от полного приращения
Δf = f (x + Δx, y + Δy, z + Δz,…) - f (x, y, z, …)
на величину, бесконечно малую по сравнению с
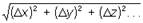
Касательная плоскость к поверхности
(X, Y, Z - текущие координаты точки на касательной плоскости;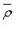 
- радиус-вектор этой точки; x, y, z - коодинаты точки касания (соответственно для нормали); 
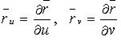- касательные векторы к координатным линиям соответственно v = const; u = const; 
)
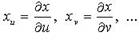1. 
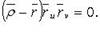
2. 
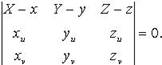
3. 
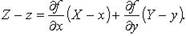
4. 
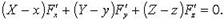
Нормаль к поверхности
1. 
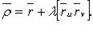
2. 
3. 
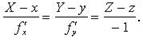
4. 
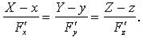
Понятие дифференциала. Геометрический смысл дифференциала. Инвариантность формы первого дифференциала.
Рассмотрим функцию y = f(x), дифференцируемую в данной точке x. Приращение Dy ее представимо в виде
D y = f'(x)D x +a (D x) D x,
где первое слагаемое линейно относительно Dx, а второе является в точке Dx = 0 бесконечно малой функцией более высокого порядка, чем Dx. Если f'(x)№ 0, то первое слагаемое представляет собой главную часть приращения Dy. Эта главная часть приращения является линейной функцией аргумента Dx и называется дифференциалом функции y = f(x). Если f'(x) = 0, то дифференциал функции по определению считается равным нулю.
Определение 5 (дифференциал). Дифференциалом функции y = f(x) называется главная линейная относительно Dx часть приращения Dy, равная произведению производной на приращение независимой переменной
dy = f'(x)Dx.
Заметим, что дифференциал независимой переменной равен приращению этой переменной dx = Dx. Поэтому формулу для дифференциала принято записывать в следующем виде: dy = f'(x)dx. (4)
Выясним каков геометрический смысл дифференциала. Возьмем на графике функции y = f(x) произвольную точку M(x,y) (рис21.). Проведем касательную к кривой y = f(x) в точке M, которая образует угол f с положительным направлением оси OX, то есть f'(x) = tgf. Из прямоугольного треугольника MKN
KN = MNtgf = D xtg f = f'(x)D x,
то есть dy = KN.
Таким образом, дифференциал функции есть приращение ординаты касательной, проведенной к графику функции y = f(x) в данной точке, когда x получает приращение Dx.
Отметим основные свойства дифференциала, которые аналогичны свойствам производной.
1. d c = 0;
2. d(c u(x)) = c d u(x);
3. d(u(x) ± v(x)) = d u(x) ± d v(x);
4. d(u(x) v(x)) = v(x) d u(x) + u(x)d v(x);
5. d(u(x) / v(x)) = (v(x) d u(x) - u(x) d v(x)) / v2(x).
Укажем еще на одно свойство, которым обладает дифференциал, но не обладает производная. Рассмотрим функцию y = f(u), где u = f (x), то есть рассмотрим сложную функцию y = f(f(x)). Если каждая из функций f и f являются дифференцируемыми, то производная сложной функции согласно теореме ( 3) равна y' = f'(u)· u'. Тогда дифференциал функции
dy = f'(x)dx = f'(u)u'dx = f'(u)du,
так как u'dx = du. То есть dy = f'(u)du. (5)
Последнее равенство означает, что формула дифференциала не изменяется, если вместо функции от x рассматривать функцию от переменной u. Это свойство дифференциала получило название инвариантности формы первого дифференциала.
Замечание. Отметим, что в формуле ( 4) dx = Dx, а в формуле ( 5) du яляется лишь линейной частью приращения функции u.
Интегральное исчисление — раздел математики, в котором изучаются свойства и способы вычисления интегралов и их приложения. И. и. тесно связано с дифференциальным исчислением и составляет вместе с ним одну из основных частей
Дата добавления: 2018-05-12; просмотров: 1196; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!