Интегрирование тригонометрических функций
Хорошо известно, что, например, решение тригонометрических уравнении можно получить многими способами: один - простой, но рутинный, а другой - трудный, но оригинальный. Т.е. для того, чтобы 'увидеть' оригинальный способ решения, нужно хорошо ориентироваться во всем множестве формул тригонометрии и знать специальные методы решения. Также обстоит дело и в интегрировании тригонометрических выражений, т.е. необходимо помнить много формул и свойств тригонометрии.
При интегрировании тригонометрических функций используются приемы, позволяющие понижать степени, избавляться от произведения и т.д., т.е. необходимо использовать тригонометрические формулы, часто приходится использовать определения 
и 
, как функции отношения 
к 
и к соответственно, для эффективной замены переменных.
Приведем основные формулы, необходимые для взятия неопределенных интегралов от тригонометрических функций.
Для понижения четных степеней используются следующие формулы:
Для избавления от произведения используются следующие формулы:
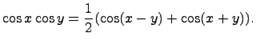
Также нужно помнить формулы двойных углов:
Интегрирование иррациональных выражений
Найдём неопределённый интеграл от иррационального выражения
Избавимся в первую очередь от иррациональности в числителе, домножив числитель и знаменатель подкоренного выражения на x − 1:
Первый интеграл является табличным, и найти его можно с помощью подстановки Чебышева:
|
|
|
I₁ = ∫dx/√(x² − 1) = ln|x + √(x² − 1)| + C
Во втором интеграле домножим числитель и знаменатель подынтегрального выражения на x:
Применим теперь подстановку t² = x² − 1. Тогда x² = 1 + t²; x·dx = t·dt
I₂ = ∫dt/(1 + t²) = arctgt = arctg√(x² − 1)
Окончательно:
I = ln|x + √(x² − 1)| − arctg√(x² − 1) + C
13. –
Интегрирование дифференциального бинома
Постановка задачи. Найти неопределенный интеграл
где 
– рациональные числа.
План решения. Выражение 
называется дифференциальным биномом. Условия его интегрируемости в элементарных функциях получены П.Л. Чебышевым. Интеграл
выражается через конечную комбинацию элементарных функций в следующих трех случаях:
1) 
– целое число; в этом случае данный интеграл вычисляется простым разложением;
2) 
– целое число; в этом случае подстановка 
, где 
– знаменатель дроби , приводит к интегралу от рациональной функции.
3) 
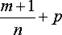– целое число; в этом случае подстановка 
, где – знаменатель дроби , приводит к интегралу от рациональной функции.
Задача 13. Найти неопределенные интегралы.
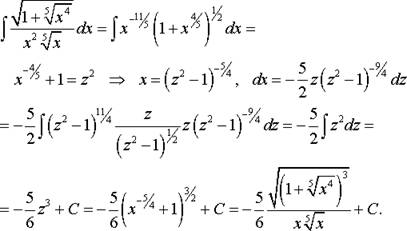
Интегрирование иррациональных функций
Для интегрирования иррациональной функции, содержащей 
используется подстановка 
.
|
|
|
Чтобы проинтегрировать иррациональную функцию, содержащую несколько рациональных степеней x, применяется подстановка в форме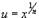 
, где n полагается равным наименьшему общему кратному знаменателей всех дробных степеней, входящих в данную функцию.
Рациональная функция x под знаком корня n-ой степени, т.е. выражение вида 
, интегрируется с помощью подстановки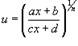 
.
Интегрирование иррациональных функций, содержащих 
и 
, рассматривается на странице Тригонометрические и гиперболические подстановки
Пример 1
Найти интеграл 
.
Решение.
Сделаем подстановку:
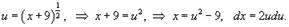
Вычислим интеграл
(ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ)
16.Постановка задачи— точная формулировка условий задачи с описанием входной и выходной информации.
Входная информация по задаче — данные, поступающие на вход задачи и используемые для её решения.
Выходная информация может быть представлена в виде документов, кадров на экране монитора, информации в базе данных, выходного сигнала устройству управления.
Постановка задачи разрабатывается организацией, разработчиком программной продукции, на основании технического задания совместно с заказчиком. Главный исполнитель — это разработчик.
|
|
|
Формула Ньютона-Лейбница
Формула Ньютона-Лейбница относится к математическому анализу и является основной формулой интегрального исчисления!
Ранее, когда мы рассматривали Формулу бинома Ньютона, мы сказали что Исааку Ньютону принадлежит роль "Отца современной математики". Ньютон вместе с Лейбницем, Огюстеном Коши, Кантором, Леонардом Эйлером и другими заложили основы современного дифференциального и интегрального исчисления, хотя строгое и стройное построение математического анализа возникло несколько позже.
Благодаря формуле Ньютона-Лейбница устанавливается связь между определенным и неопределенным интегралом. А именно:
Чтобы решить определенный интеграл, надо сначала вычислить неопределенный интеграл (или найти первообразную), а затем вычислить определенный интеграл, подставив первообразную подынтегральной функции в формулу Ньютона-Лейбница:
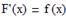
Здесь F(x) - первообразная для функции f(x)! Таким образом, чтобы применить формулу Ньютона-Лейбница, надо вычислить значение первообразной при верхнем пределе интегрирования B, при нижнем пределе интегрирования - A, а затем взять их разность F(b)-F(a). Вначале мы рассмотрим доказательство данной формулы, а затем приведем Примеры решения интегралов по основной формуле интегрального и дифференциального исчисления.
|
|
|
Дата добавления: 2018-05-12; просмотров: 475; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!