Оценка знакочередующегося ряда.
Ряд называется знакочередующимся, если его члены попеременно принимают значения противоположных знаков, т. е.:
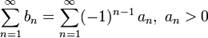
Оценка остатка ряда Лейбница
Из доказательства признака Лейбница следует, что сумма знакопеременного сходящегося ряда меньше по модулю первого члена остатка ряда. Поскольку любой остаток ряда rn является также рядом Лейбница, то для него справедливо:
.
Знакопеременные ряды
Определение 5. Числовые ряды, содержащие как положительные, так и отрицательные члены, называются знакопеременными рядами.
Ряды, все члены которых отрицательные числа, не представляют нового по сравнению со знакоположительными рядами, так как они получаются умножением знакоположительных рядов на –1.
Изучение знакопеременных рядов начнём с частного случая – знакочередующихся рядов.
Определение 6. Числовой ряд вида u1-u2+u3-u4+…+ +(-1)n-1.un+…, где un – модуль члена ряда, называется знакочередующимся числовым рядом.
Теорема 9. (Признак Лейбница)
Если для знакочередующегося числового ряда
(19)
Выполняются два условия:
Члены ряда убывают по модулю u1>u2>…>un>…,
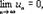
то ряд (19) сходится, причём его сумма положительна и не превосходит первого члена ряда.
Доказательство. Рассмотрим частичную сумму чётного числа членов ряда S2n=(u1-u2)+(u3-u4)+…+(u2n-1-u2n).
По условию u1>u2>…>u2n-1>u2n, то есть все разности в скобках положительны, следовательно, S2n возрастает с возрастанием n и S2n>0 при любом n.
|
|
|
С другой стороны S2n=u1-[(u2-u3)+(u4-u5)+…+(u2n-2-u2n-1)+u2n]. Выражение в квадратных скобках положительно и S2n>0, поэтому S2n<u1 для любого n. Таким образом, последовательность частичных сумм S2n возрастает и ограничена, следовательно, существует конечный 
S2n=S. При этом 0<S≤u1.
Рассмотрим теперь частичную сумму нечётного числа членов ряда S2n+1=S2n+u2n+1. Перейдём в последнем равенстве к пределу при n→∞: S2n+1= S2n+ u2n+1=S+0=S. Таким образом, частичные суммы как чётного, так и нечётного числа членов ряда имеют один и тот же предел S, поэтому Sn=S, то есть данный ряд сходится. Теорема доказана
Абсолютная и условная сходимость
Ряд 
называется абсолютно сходящимся, если 
сходится. Абсолютно сходящийся ряд сходится.
Если ряд сходится, а расходится, то ряд называется сходящимся условно. Для таких рядов верна теорема Римана о перестановке членов условно сходящегося ряда.
Знакопеременные ряды
Ряд, содержащий как положительные, так и отрицательные члены, называется знакопеременным.
Знакочередующимся называется ряд вида
, где 
.
Ряды вида 
также называются знакочередующимися.
Признак абсолютной сходимости
Знакопеременный ряд
(4)
сходится, если сходится ряд
|
|
|
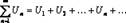(5)
Ряд (4) называется в этом случае абсолютно сходящимся. Если ряд (4) сходится, а ряд (5) расходится, то ряд (4) называется условно сходящимся. При этом сходимость ряда (4) можно в ряде случаев установить без исследования ряда (5).
Признак сходимости Лейбница
Пусть имеется знакочередующийся ряд 
.
Если одновременно выполняются следующие два условия:
1) 
,
2) 
, то такой ряд сходится и его сумма не превосходит первого члена: 
.
16.Функциональный ряд— ряд, каждым членом которого, в отличие от числового ряда, является не число, а функция 
.
Функциональный ряд
— n-ная частичная сумма.
Сходимость
Ряд называется сходящимся поточечно, если последовательность 
его частичных сумм сходится поточечно.
Ряд называется сходящимся равномерно, если последовательность его частичных сумм сходится равномерно.
Дата добавления: 2018-05-12; просмотров: 580; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!