Квадратурные формулы Ньютона-Котеса
Если в интеграл 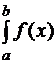 вместо функции
вместо функции  подставить ее интерполирующий многочлен Лагранжа
подставить ее интерполирующий многочлен Лагранжа 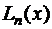 , то получим семейство квадратурных формул Ньютона-Котеса
, то получим семейство квадратурных формул Ньютона-Котеса
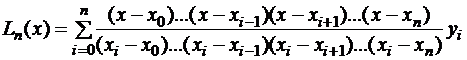 .
.
Для равноотстоящих узлов полином Лагранжа будет:
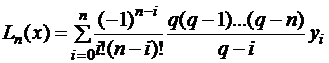 ,
,
где 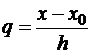 – шаг интерполяции,
– шаг интерполяции, 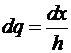 ,
, 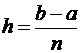 тогда:
тогда:
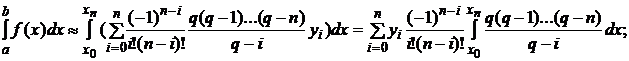
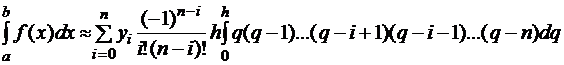 ;
;
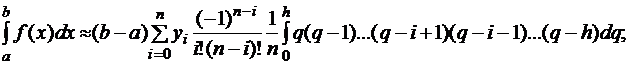
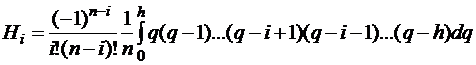 ;
; 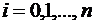 .
.
Здесь 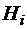 – коэффициенты Ньютона-Котеса. Они не зависят от
– коэффициенты Ньютона-Котеса. Они не зависят от  , а зависят только от числа узлов интерполяции
, а зависят только от числа узлов интерполяции  , следовательно
, следовательно
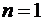 ,
, 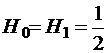 ;
;
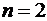 ,
, 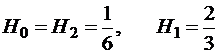 ;
;
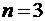 ,
, 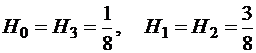 ;
;
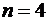 ,
, 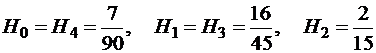 .
.
Тогда формула Ньютона-Котеса имеет вид:
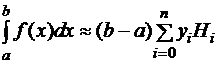 .
.
Частный случай 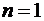 :
:
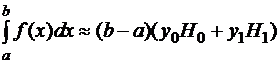 ;
;
 ,
, 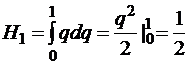 ,
,
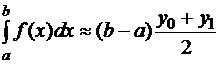 – формула трапеций.
– формула трапеций.
Частный случай 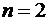 ,
, 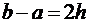 :
:
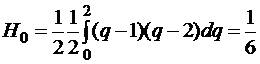 ,
, 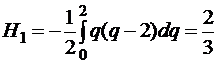 ,
,
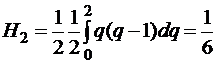 ,
, 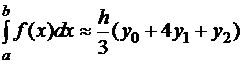 – формула Симпсона. Аналогично при
– формула Симпсона. Аналогично при 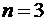 получим формулу трех восьмых:
получим формулу трех восьмых:
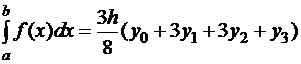 .
.
Погрешность формулы трех восьмых на шаге 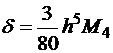 .
.
Экстраполяция по Ричардсону
Пусть 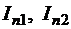 – два приближенных значения интеграла
– два приближенных значения интеграла 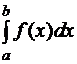 , вычисленных по одной и той же формуле при
, вычисленных по одной и той же формуле при 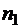 и
и 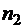
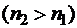 . Тогда более точное значение этого интеграла можно найти:
. Тогда более точное значение этого интеграла можно найти:
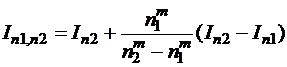 ,
,
где m – порядок погрешности на одном шаге выбранной формулы.
Для формулы трапеций m = 2, формулы Симпсона – m = 4.
Квадратурные формулы Гаусса, Чебышева
Общий вид квадратурной формулы:
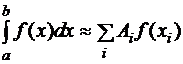 (3.1)
(3.1)
здесь  – узлы интегрирования,
– узлы интегрирования, 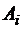 – весовые функции. Определенный интеграл приближенно равен средневзвешенному значений подынтегральной функции, вычисленных в определенных точках промежутка интегрирования.
– весовые функции. Определенный интеграл приближенно равен средневзвешенному значений подынтегральной функции, вычисленных в определенных точках промежутка интегрирования.
В предыдущих квадратурных формулах брались равноотстоящие узлы с шагом  , и весовые коэффициенты получались заменой подынтегральной функции на кусочно-постоянную (формула прямоугольников), кусочно-линейную (формула трапеций), кусочно-квадратичную ( формула Симпсона).
, и весовые коэффициенты получались заменой подынтегральной функции на кусочно-постоянную (формула прямоугольников), кусочно-линейную (формула трапеций), кусочно-квадратичную ( формула Симпсона).
|
|
|
Для получения более точных формул откажемся от равномерного распределения узлов. Удобно сделать замену:
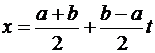 ,
, 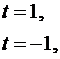
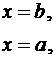
тогда интеграл по произвольному промежутку 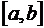 преобразуется в интеграл по стандартному промежутку
преобразуется в интеграл по стандартному промежутку 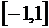 :
:
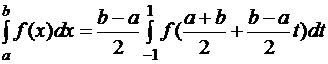 .
.
Таким образом, без потери общности можно рассматривать интеграл:
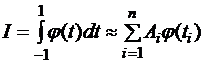 , (3.2)
, (3.2)
здесь  – число узлов интегрирования.
– число узлов интегрирования.
В выражение для погрешности квадратурных формул входит производная некоторого порядка от функции, т. к. производная порядка  равна нулю
равна нулю 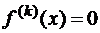 для полинома степени
для полинома степени 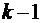 , то квадратурная формула верна для многочленов степени (k – 1). Например, формула односторонних прямоугольников точна для полиномов нулевого порядка,
, то квадратурная формула верна для многочленов степени (k – 1). Например, формула односторонних прямоугольников точна для полиномов нулевого порядка, 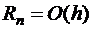 ; формула центральных прямоугольников – для линейных полиномов, формула трапеций – для линейных полиномов,
; формула центральных прямоугольников – для линейных полиномов, формула трапеций – для линейных полиномов, 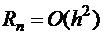 ; формула Симпсона – для кубических полиномов,
; формула Симпсона – для кубических полиномов, 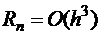 .
.
Потребуем, чтобы квадратурная формула (3.2) была точна для полинома степени  , где
, где  – число узлов.
– число узлов.
Формула Чебышева
Пусть все весовые коэффициенты равны 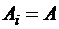 . Получим формулу Чебышева, точную для полиномов степени
. Получим формулу Чебышева, точную для полиномов степени  . Считая, что равенство (3.2) будет точным для функций
. Считая, что равенство (3.2) будет точным для функций 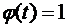 , имеем:
, имеем: 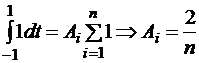 , тогда квадратурная формула примет вид:
, тогда квадратурная формула примет вид:
|
|
|
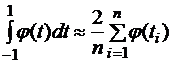 . (3.3)
. (3.3)
Подставим в формулу (3.3) 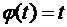 и, считая равенство (3.3) точным, получим уравнение :
и, считая равенство (3.3) точным, получим уравнение : 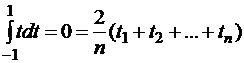 .
.
Подставляя поочередно 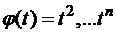 , получим систему уравнений:
, получим систему уравнений:
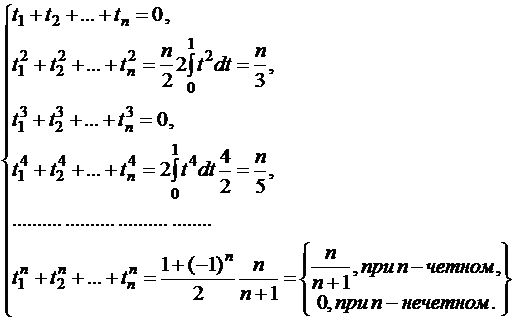 (3.4)
(3.4)
Доказано, что эта специфическая система  уравнений с
уравнений с  неизвестными (3.4) определяет единственный набор
неизвестными (3.4) определяет единственный набор 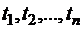 при
при 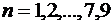 . Эти узлы вычислены с высокой точностью и затабулированы. При
. Эти узлы вычислены с высокой точностью и затабулированы. При 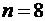 и
и 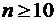 система (3.4) не имеет действительных решений.
система (3.4) не имеет действительных решений.
Формула Гаусса
Рассмотрим общий вид квадратурной формулы (3.2). В ней неизвестными являются 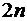 параметров:
параметров:  узлов
узлов 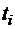 и
и  весовых коэффициентов
весовых коэффициентов 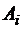 .
.
Подберем 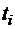 и
и 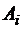 так, чтобы равенство
так, чтобы равенство 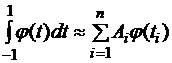 было точным для полиномов степени
было точным для полиномов степени 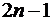 или для степенных функций:
или для степенных функций:
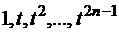 .
.
Подставляя в точное равенство (3.2) поочередно эти функции, получим:
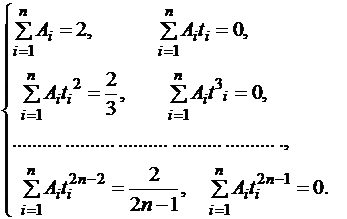
 (3.5)
(3.5)
Решение системы (3.5) весьма затруднительно, но, оказывается, узлами квадратурной формулы в этом случаеявляются корни полиномов Лежандра 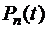 , которые принадлежат интервалу
, которые принадлежат интервалу 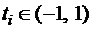 и расположены симметрично относительно начала координат, а веса
и расположены симметрично относительно начала координат, а веса 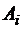 находятся интегрированием базисных многочленов Лагранжа
находятся интегрированием базисных многочленов Лагранжа 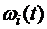 степени
степени 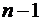 :
:
|
|
|
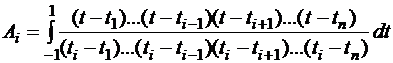 . (3.6)
. (3.6)
Напомним, что полиномы Лежандра определяются рекуррентной формулой Родрига:
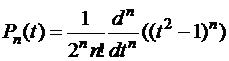
и являются ортогональными полиномами с весом 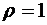 на отрезке
на отрезке 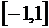
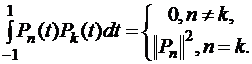
Докажем, что при таких 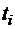 и
и 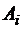 формула (3.2) будет точна при подстановке в нее вместо
формула (3.2) будет точна при подстановке в нее вместо 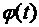 любого многочлена степени
любого многочлена степени 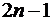 .
.
Пусть 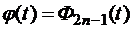 . Согласно теореме о делении полинома
. Согласно теореме о делении полинома 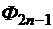 на полином
на полином 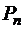 с остатком, существуют такие полиномы
с остатком, существуют такие полиномы 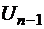 и
и 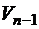 , что:
, что:
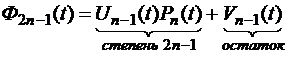 .
.
Подставим это выражение в левую часть формулу (3.2).В силу линейной независимости полиномов Лежандра 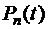 и их попарной ортогональности всегда найдется набор
и их попарной ортогональности всегда найдется набор 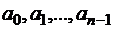 , таких, что
, таких, что
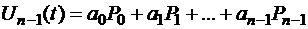 ,
,
тогда
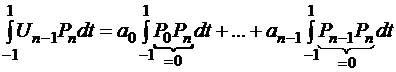 ,
,
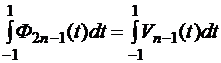 . (3.7)
. (3.7)
Теперь преобразуем правую часть формулы (3.1):
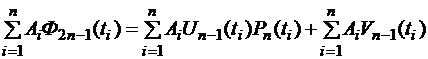 ,
,
здесь 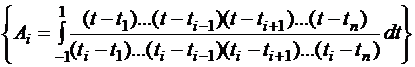 – базисный многочлен Лагранжа. Покажем, что при таком
– базисный многочлен Лагранжа. Покажем, что при таком 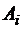 формула будет точна:
формула будет точна:
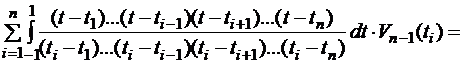
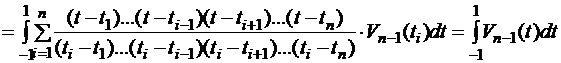 .
.
В левой части последнего равенства под интегралом стоит интерполяционный многочлен Лагранжа степени 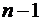 , составленный по
, составленный по  значениям
значениям 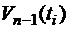 , который в силу своей единственности однозначно восстанавливается интерполированием. Тогда верно точное равенство:
, который в силу своей единственности однозначно восстанавливается интерполированием. Тогда верно точное равенство:
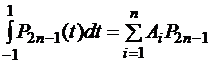 .
.
Отсюда ясно, что указанные значения 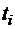 и
и 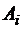 являются узлами и весовыми коэффициентами квадратурной формулы Гаусса.
являются узлами и весовыми коэффициентами квадратурной формулы Гаусса.
Запишем теперь общую квадратурную формулу для интеграла по промежутку 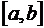 :
:
|
|
|
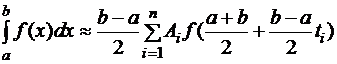 .
.
Оценка погрешности квадратурных формул Гаусса, Чебышева говорит о существенно более быстром убывании погрешности с ростом числа узлов  для достаточно гладких интегрируемых функций. При
для достаточно гладких интегрируемых функций. При 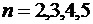 существуют таблицы (см. табл.3.1).
существуют таблицы (см. табл.3.1).
Таблица 3.1.
|
| Формула Чебышева | Формула Гаусса | ||
| 
| 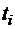
| 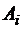
| |
| 2 | 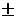 0,577350 0,577350
| 1 | 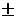 0,577350 0,577350
| 1 |
| 3 | 0
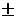 0,707107 0,707107
| 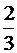
| 0
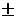 0,774597 0,774597
| 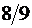
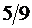
|
| 4 | 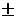 0,187592 0,187592
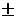 0,794654 0,794654
| 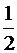
| 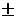 0,339981 0,339981
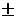 0,861136 0,861136
| 0,652145 0,347855 |
| 5 | 0
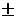 0,374541 0,374541
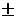 0,832497 0,832497
| 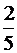
| 0
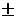 0,538469 0,538469
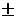 0,906180 0,906180
| 0,568889 0,478629 0,236927 |
В практикуме рассмотрены примеры вычисления интегралов по квадратурным формулам прямоугольников, трапеций, Симпсона, формулам Гаусса и Чебышева для 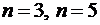 с помощью вычислительного пакета Mathcad. Очевидно, что использование формул Гаусса и Чебышева позволяет достичь высокой точности при существенно меньшем объеме вычислений в сравнении с другими квадратурными формулами.
с помощью вычислительного пакета Mathcad. Очевидно, что использование формул Гаусса и Чебышева позволяет достичь высокой точности при существенно меньшем объеме вычислений в сравнении с другими квадратурными формулами.
Метод Монте-Карло
Метод статистических испытаний, или метод Монте-Карло использует статистико-вероятностный подход к вычислению определенных интегралов.
Рассматривается некоторая случайная величина 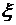 , математическое ожидание которой равно искомой величине
, математическое ожидание которой равно искомой величине  :
:
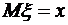 .
.
Проводится серия  независимых испытаний, в результате которых генерируется последовательность
независимых испытаний, в результате которых генерируется последовательность  случайных чисел
случайных чисел 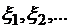 , имеющих то же распределение, что и
, имеющих то же распределение, что и 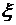 . Находится выборочное среднее
. Находится выборочное среднее 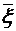 , которое является статистической оценкой
, которое является статистической оценкой 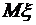 , при этом
, при этом
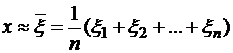 .
.
Пусть 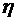 равномерно распределенная на отрезке
равномерно распределенная на отрезке 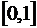 случайная величина. Это означает, что ее плотность распределения задается:
случайная величина. Это означает, что ее плотность распределения задается:
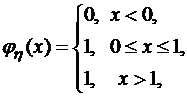
тогда любая функция 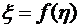 также будет случайной величиной, и ее математическое ожидание равно
также будет случайной величиной, и ее математическое ожидание равно
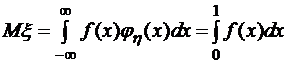 .
.
Читая это равенство в обратном порядке, получаем, что интеграл 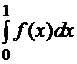 может быть вычислен как оценка математического ожидания некоторой случайной величины
может быть вычислен как оценка математического ожидания некоторой случайной величины 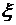 , которая является функцией случайной величины
, которая является функцией случайной величины 
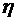 с равномерным законом распределения, причем оценка
с равномерным законом распределения, причем оценка 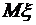 определяется независимыми реализациями
определяется независимыми реализациями 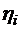 случайной величины
случайной величины 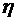 :
:
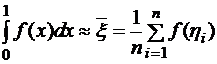
или для интеграла общего вида
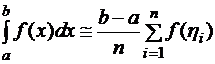 ,
, 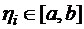 .
.
Погрешность метода 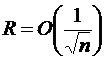 .
.
Рулетка Монте-Карло – простейший генератор случайных чисел.
Для использования метода Монте-Карло необходимо генерировать последовательности случайных чисел с заданным законом распределения. Способы генерирования: разработаны алгоритмы генерирования случайных чисел, датчики случайных чисел, реализованные в виде программ.
Дата добавления: 2018-05-12; просмотров: 699; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
