Интерполяционный многочлен Лагранжа
Наиболее распространенным и практически важным случаем является задание связи между параметрами 
и 
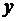в виде некоторой таблицы 
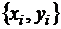. Это означает, что дискретному множеству значений аргумента 
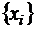поставлено в соответствие множество значений функции 
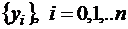. Табличные значения могут быть результатами эксперимента или расчета. Вид точной функции, отражающей зависимость 
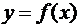нам не известен. Мы хотим
по имеющимся табличным данным построить другую функцию 
, которая была бы в некотором смысле близкой к 
и достаточно простой.
Задача приближения функций называется задачей аппроксимации, функция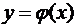 
– аппроксимирующей. Аппроксимация, при которой приближение строится на заданном дискретном множестве точек 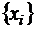, называется точечной.
Процесс вычисления значений функции в точках , отличных от значений 
, называется интерполяцией. Если аргумент находится за пределами отрезка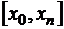 
, то задача определения значения функции в точке называется экстраполированием.
Пусть задана система точек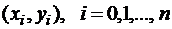 
, всего 
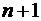значений некоторой функции . Требуется построить функцию такую, что ее значения в точках , называемых узлами интерполяции, совпадали с заданными значениями функции:
, 
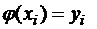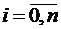, т.е.
требуется строгое совпадение значений функций в узлах интерполяции. Геометрически это означает, что график интерполирующей функции 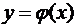проходит через заданные точки.
Будем искать интерполирующую функцию в виде канонического многочлена степени 
|
|
|
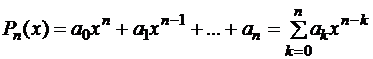. (2.1)
Полагая, что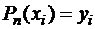 
, получим:
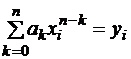
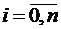. (2.2)
Таким образом, чтобы многочлен (2.1) был интерполяционным, нужно, чтобы его коэффициенты удовлетворяли системе уравнений:
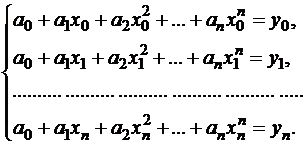(2.3)
Получили систему линейных уравнений порядка (n + 1), её определитель
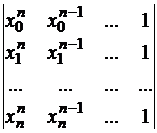
так называемый определитель Вандермонда, не равен нулю, если все различны, следовательно, существует единственный интерполирующий многочлен канонического вида (2.1). Однако практическое построение интерполяционного многочлена таким путем малоэффективно.
Построим интерполирующий полином Лагранжа в виде линейной комбинации:
,
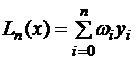где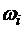 
– базисные полиномы такие, что:
.
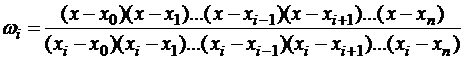Значение базисного полинома в узлах интерполяции будет:
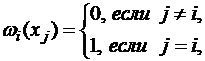
тогда интерполяционный многочлен Лагранжа имеет вид:
.
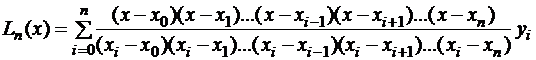При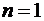 
по двум точкам построим линейный многочлен:
.
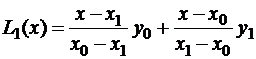При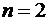 
по трем точкам построим многочлен Лагранжа второй степени:
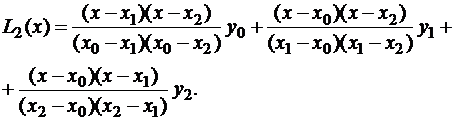
Погрешность интерполяции полинома Лагранжа
Оценим погрешность приближенного представления функции интерполяционным многочленом Лагранжа на рассматриваемом отрезке 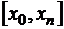как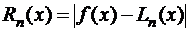 
. Рассмотрим вспомогательную функцию
|
|
|
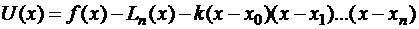. (2.3)
В точках , 
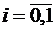будет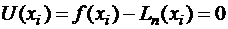 
,следовательно, 
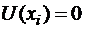, значит функция 
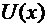имеет по меньшей мере (n + 1) нулей на рассматриваемом отрезке.
Пусть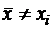 
, 
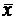не совпадает ни с одной точкой. Подберем значение 
так, чтобы функция в этой точке имела еще один корень:
.
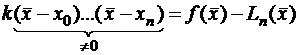Следовательно, можно подобрать единственное значение коэффициента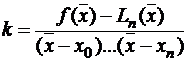 
так, чтобы 
, 
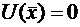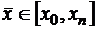, тогда 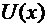имеет по крайней мере (n + 2) корней. По теореме Ролля между нулями функции существует, по крайней мере, один нуль производной, тогда производная 
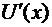имеет (n + 1) нуль. Применим теорему Ролля к производной, тогда 
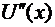имеет нулей и т.д. Производная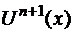 
имеет один корень, следовательно, существует точка 
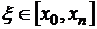такая, что 
.
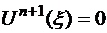Продифференцируем равенство (2.3) (n + 1) раз:
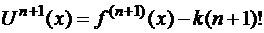
Следовательно, учитывая, что 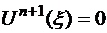, получим 
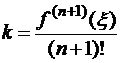. Поскольку 
– любая точка из промежутка, не совпадающая с узловой, то заменим ее произвольной точкой , тогда:
. 
.
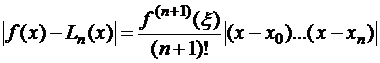Если производная порядка 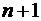ограничена 
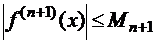, то оценка погрешности полиномиальной интерполяции:
.
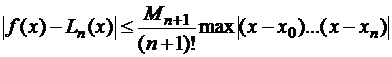Рассмотрим линейную интерполяцию
,
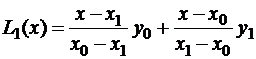если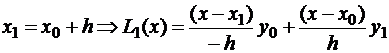 
.
Оценим погрешность линейной интерполяции, для этого найдем :
,
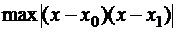Преобразуем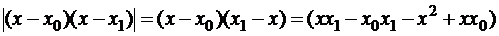 
.
Найдем точку, в которой производная этого выражения имеет нуль:
|
|
|
,
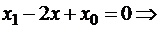
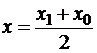тогда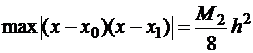 
и оценка погрешности имеет вид:
.
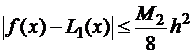Многочлены Чебышева
Многочленом Чебышева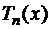 
, 
, 
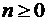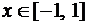называется функция
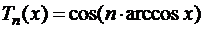
Подставим 
, 
, , 
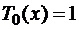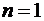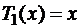–два первых полинома. Из тригонометрии известно тождество:
.
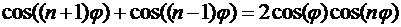Сделаем замену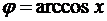 
и подставим в выражение:
,
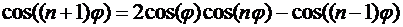тогда получим выражение
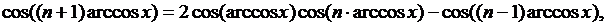
из которого, используя определение, получим рекуррентную формулу:
.
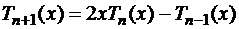Подставляя известные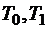 
, получим последовательность полиномов:
;
;
;
.
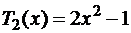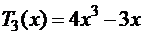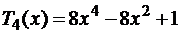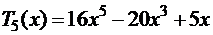На рис. 2.1 изображены графики первых полиномов Чебышева.
 |
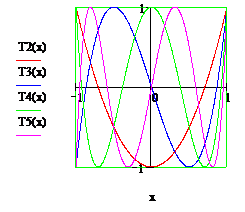
Свойства полиномов Чебышева
1. Полиномы четного порядка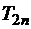 
– четные функции; нечетного порядка 
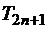– нечетные.
2. Коэффициент при старшей степени полинома Чебышева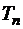 
при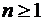 
равен 2n–1 (следствие рекуррентной формулы).
3. Полином 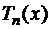степени имеет n действительных корней на интервале (-1, 1), найдем их:
.
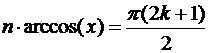Откуда нули полинома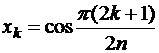 
; k = 0, 1,…, (n – 1)расположены неравномерно на интервале 
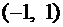и сгущаются к его концам.
4. Полиномы Чебышева ограничены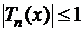 
для 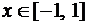. Максимум модуля полинома 
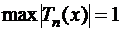достигается в точках:
,
, 
,
,
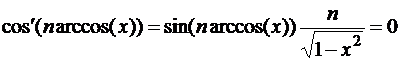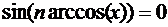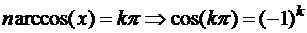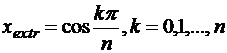т. е. 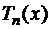имеет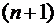 
максимумов (минимумов) на[-1, 1].
5. Многочлен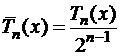 
среди всех многочленов -ой степени
со старшим коэффициентом при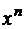 
равным единице, имеет на отрезке [-1, 1] наименьшее значение максимума модуля. 
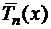называется многочленом, наименее уклоняющимся от нуля.
|
|
|
Докажем, что не существует полином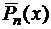 
n-ой степени со старшим коэффициентом равным единице, такой, что
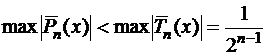(2.4)
Будем доказывать методом отпротивного: предположим, что существует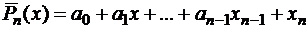 
, удовлетворяющий неравенству (2.4)такой, чторазность 
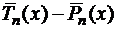–многочлен степени, не выше 
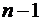, причем 
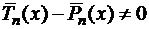. Кроме этого, в 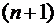точках, являющихся точками экстремумов 
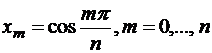, эта разность принимает отличные от нуля значения с чередующимися знаками в силу того, что 
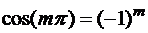. Тогда 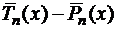–многочлен степени меньше чем n, обращается в ноль, по крайней мере, в n точках, что невозможно.
Другой вид полиномов Чебышева:
.
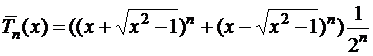Пусть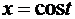 
.
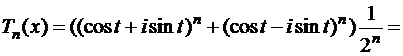
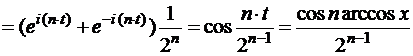Минимизация погрешности интерполяции полинома
Лагранжа
Погрешность интерполяции полинома Лагранжа имеет вид:
.
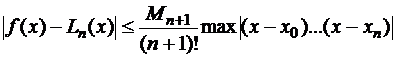Как выбрать узлы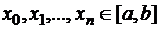 
так, чтобы максимальная погрешность интерполяции была минимальной? Следует выбрать такое расположение узлов, чтобы 
.
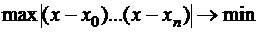Рассмотрим отрезок [-1, 1] и , наименее уклоняющийся от нуля.
Возьмем в качестве узлов 
корни полинома 
:
; 
.
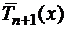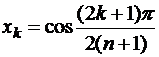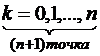При этом базисные полиномы Лагранжа будут:
,
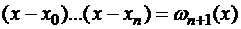тогда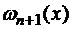 
будет пропорциональна 
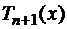или
;
.
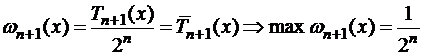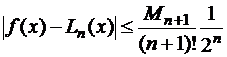В силу свойств полиномов Чебышева, наименее уклоняющихся от нуля, улучшить эту оценку погрешности за счет выбора других узлов нельзя. При любом выборе узлов интерполяции не совпадающих с корнями 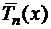, оценка будет хуже, т. е. эта оценка является оптимальной.
Произвольный отрезок [a, b] можно отобразить на отрезок [–1, 1] заменой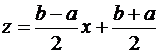 
;
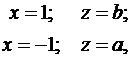
тогда полиномы преобразуются по формуле
.
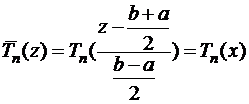Узлы интерполяции будут:
;
.
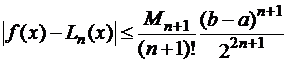Оптимальное распределение узлов является неравномерным – они сгущаются к концам и разрежены в середине.
При большом числе точек получаем интерполяционный полином Лагранжа высокой степени, который трудно использовать для практических вычислений. Можно разбить промежуток 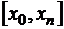на части и на каждой использовать полином Лагранжа невысокой степени. В точках сшивки функция будет непрерывной, но производная будет иметь разрыв.
Дата добавления: 2018-05-12; просмотров: 724; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!