Численное дифференцирование. Аппроксимационные формулы
Пусть некоторая, достаточное число раз дифференцируемая, функция 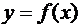 задана на промежутке [a; b]. Число
задана на промежутке [a; b]. Число  – целое,
– целое, 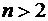 . Разделим отрезок [a; b] на
. Разделим отрезок [a; b] на  равных частей длины
равных частей длины 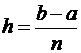 ,
,  – шаг разбиения. Пронумеруем узловые точки
– шаг разбиения. Пронумеруем узловые точки 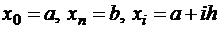 ,
,  меняется от 0 до
меняется от 0 до  . Обозначим
. Обозначим 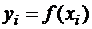 .В классической формуле Тейлора
.В классической формуле Тейлора
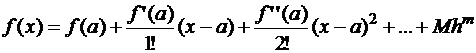
возьмем сначала в качестве 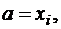
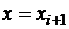 ,
, 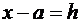 , а затем выбираем
, а затем выбираем 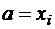 ,
, 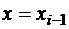 ,
, 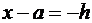 .
.
Получились две формулы:
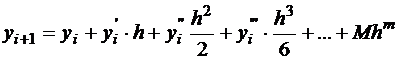 ; (1.1)
; (1.1)
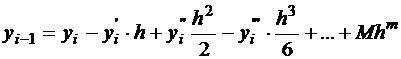 . (1.2)
. (1.2)
Константы M в этих формулах не обязаны быть одинаковыми, а кроме того, они меняются в зависимости от количества учитываемых слагаемых
в формуле Тейлора, но мы обозначаем их одинаково, не учитывая знака и величины. Из формулы (1.1) можно получить приближенное значение первой производной в точке xi
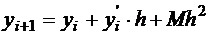 ;
;
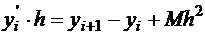 .
.
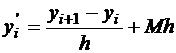 – это аппроксимационная формула для y'i справа, первого порядка точности, т.к. ее погрешность
– это аппроксимационная формула для y'i справа, первого порядка точности, т.к. ее погрешность 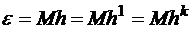 , k = 1.
, k = 1.
Эту формулу можно получить непосредственно из определения производной 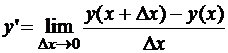 .
.
Заменим в определении Δх наименьшим возможным положительным значением Δх=h:
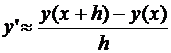 , или для
, или для 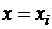 :
: 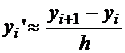 ,
,
но в этом случае ничего нельзя сказать о величине погрешности и о порядке точности формулы.
Из формулы (1.2) точно так же получается 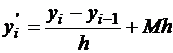 – это аппроксимация первой производной слева, она также 1-го порядка точности.
– это аппроксимация первой производной слева, она также 1-го порядка точности.
Можно получить аппроксимацию первой производной более высокого порядка точности. Для этого вычтем из формулы (1.1) формулу (1.2)
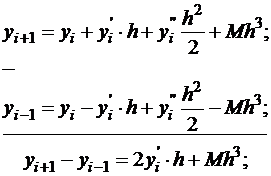
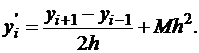
Получилась аппроксимация 2-го порядка. Можно получить аппроксимацию первой производной любого порядка точности. Для этого нужно записать еще несколько вариантов формулы Тейлора для 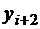 ,
, 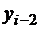 и т.д.,
и т.д.,
а затем взять их линейную комбинацию так, чтобы слагаемые с h2, h3…hk
сократились.
|
|
|
Можно аналогично получить аппроксимацию для производных высших порядков. Например, y''=(y')', значит
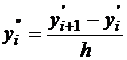 , где
, где 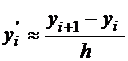 ,
, 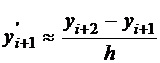 , тогда
, тогда
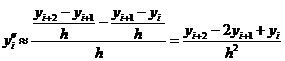
Но эта формула приближенная и ничего не известно об ее погрешности.
Можно поступить иначе, запишем два варианта формулы Тейлора:
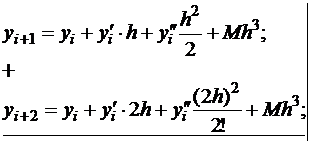
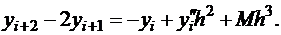
Сложим эти уравнения, умножив предварительно второе на -2, получим
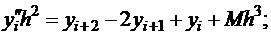
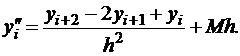
Полученная формула имеет 1-ый порядок точности.
Если этот результат не устраивает исследователя, то можно получить более точную аппроксимацию. Запишем два варианта формулы Тейлора, формулы (1.1) и (1.2)
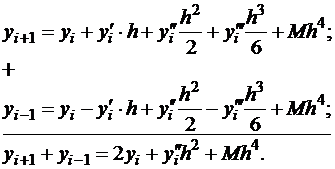
После сложения получается
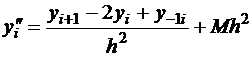 – аппроксимационная формула 2-го порядка. Для вычисления второй производной нужно знать значения функции
– аппроксимационная формула 2-го порядка. Для вычисления второй производной нужно знать значения функции
в трех соседних узлах. Можно получить еще более точную формулу
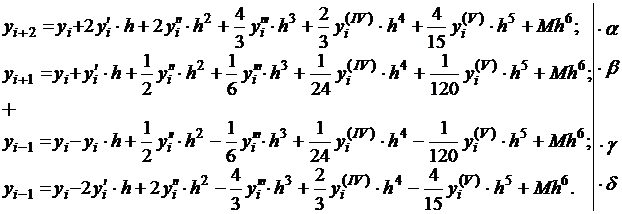
Умножим каждую из формул на соответствующие множители α, β, γ и δ и сложим. При этом подберем множители так, чтобы слагаемые с y'i, y'''i, y(IV)i сократились, т.е.
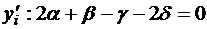 ;
;
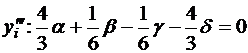 ;
;
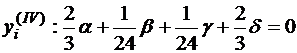 .
.
Получилась система из 3-х линейных уравнений с 4-мя неизвестными (значит, одно из неизвестных можно выбрать произвольно):
|
|
|
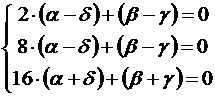 .
.
Из первых двух уравнений получим, что α – δ = 0 и β – γ = 0, α = δ, β = γ, 16(2α) + (2β) = 0, β = -162, γ = -162, δ = α. Выбираем произвольным образом α = 1, тогда получим следующие значения β = -16, γ = -16, δ = 1.
Складываем все четыре уравнения, умноженные на соответствующие коэффициенты:
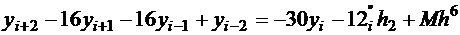 ;
;
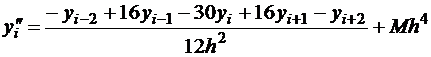 .
.
Эта аппроксимационная формула для второй производной более громоздкая, чем предыдущая, но она имеет более высокий порядок точности - четвертый. Для вычисления значения второй производной в  -ом узле требуется знать значения функции в этом узле и в двух соседних узлах слева
-ом узле требуется знать значения функции в этом узле и в двух соседних узлах слева
и справа. Таким способом могут быть получены формулы численного дифференцирования для производных любого порядка и оценена их точность.
Задача. Вывести одностороннюю аппроксимационную формулу 2-го порядка точности для первой производной
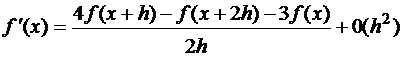 , используя разложение функции по формуле Тейлора.
, используя разложение функции по формуле Тейлора.
Задача. Вывести аппроксимационную формулу 3-го порядка точности для первой производной y'I, используя разложениефункции по формуле Тейлора в соседних узлах.
Задача Коши для обыкновенного дифференциального
уравнения 1-го порядка. Метод Эйлера
|
|
|
Обыкновенное дифференциальное уравнение первого порядка можно записать в явном виде 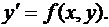 Такое уравнение в общем случае имеет бесконечно много частных решений, и для того, чтобы выбрать из них одно конкретное, ставят дополнительное условие, обычно в виде
Такое уравнение в общем случае имеет бесконечно много частных решений, и для того, чтобы выбрать из них одно конкретное, ставят дополнительное условие, обычно в виде 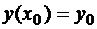 .
.
Получается задача Коши: 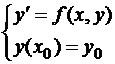 .
.
Если функция 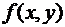 непрерывна по х и непрерывно дифференцируема по y, то задача Коши имеет единственное решение, непрерывно зависящее от начальных данных
непрерывна по х и непрерывно дифференцируема по y, то задача Коши имеет единственное решение, непрерывно зависящее от начальных данных 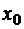 и
и 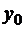 . Если
. Если 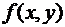 непрерывна по х и по y, то задача Коши имеет локальное решение, возможно и единственное (Теорема Пеано). Решение может существовать не во всех точках, где определена
непрерывна по х и по y, то задача Коши имеет локальное решение, возможно и единственное (Теорема Пеано). Решение может существовать не во всех точках, где определена 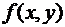 .
.
Основы численных методов вообще и для дифференциальных уравнений в частности были заложены Л. Эйлером. Его именем называется один
из самых простых методов решения задачи Коши (которая в те годы еще так не называлась, т.к. Коши лет на 50 моложе Эйлера). Метод состоит в том, чтобы заменить производную y' ее аппроксимацией. Рассмотрим решение задачи Коши на промежутке [a; b]. Обозначим: 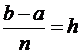 – шаг разбиения,
– шаг разбиения, 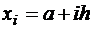 – узловые точки, x0 = a, xn = b, i = 0, 1…, n; yi = y(xi).
– узловые точки, x0 = a, xn = b, i = 0, 1…, n; yi = y(xi).
Уравнение 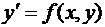 в точке xi и yi имеет вид
в точке xi и yi имеет вид 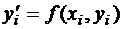 , после аппроксимации
, после аппроксимации 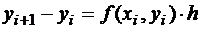 ;
;
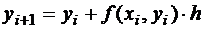 .
.
Из начальных условий 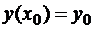 – дано. Следующее значение –
– дано. Следующее значение – 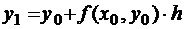 – получается из x0, y0. Дальше процесс продолжается, следующее yi+1 получается из предыдущего yi, и так до
– получается из x0, y0. Дальше процесс продолжается, следующее yi+1 получается из предыдущего yi, и так до 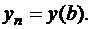 Геометрически метод Эйлера означает замену движения по кривой движением по касательной:
Геометрически метод Эйлера означает замену движения по кривой движением по касательной:
|
|
|
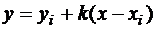 - уравнение прямой, проходящей через точку (xi, yi);
- уравнение прямой, проходящей через точку (xi, yi);
k – ее угловой коэффициент.
Для касательной угловой коэффициент 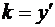 , в нашем случае
, в нашем случае 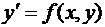 , значит,
, значит, 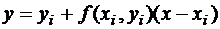 – уравнение касательной
– уравнение касательной
к интегральной кривой y=y(x) в точке x=xi y=yi, а точка 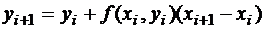 лежит на касательной при x=xi+1. Погрешность на первом шаге получается сразу из аппроксимационной формулы:
лежит на касательной при x=xi+1. Погрешность на первом шаге получается сразу из аппроксимационной формулы:
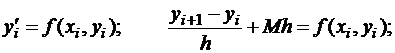
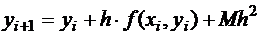 – она составляет величину второго порядка на одном шаге. Таким образом, приближенное значение функции в первом узле будет:
– она составляет величину второго порядка на одном шаге. Таким образом, приближенное значение функции в первом узле будет:
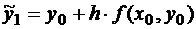 .
.
Но на втором шаге при вычислении y2
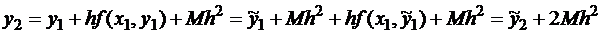 используется приближенное значение
используется приближенное значение 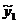 и в результате погрешности на каждом шаге складываются, в результате после n шагов вычислений погрешности суммируются
и в результате погрешности на каждом шаге складываются, в результате после n шагов вычислений погрешности суммируются 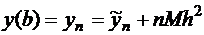 и общая погрешность будет:
и общая погрешность будет: 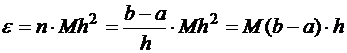 ;
; 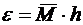 , т.е. общий результат вычислений получается 1-го порядка точности, несмотря на то, что сама расчетная формула 2-го порядка.
, т.е. общий результат вычислений получается 1-го порядка точности, несмотря на то, что сама расчетная формула 2-го порядка.
Оценка погрешности 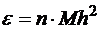 является достаточно приблизительной, т.к., во-первых, на каждом шаге при оценке погрешности Mh2 константа M не остается одинаковой, а во-вторых, при вычислениях
является достаточно приблизительной, т.к., во-первых, на каждом шаге при оценке погрешности Mh2 константа M не остается одинаковой, а во-вторых, при вычислениях 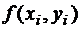 используется приближенное значение
используется приближенное значение 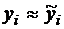 и
и 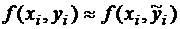 . Тем не менее, принято оценивать погрешность метода именно так, считая, что M общее – это наибольшее значение М на n шагах, а функцию можно разложить
. Тем не менее, принято оценивать погрешность метода именно так, считая, что M общее – это наибольшее значение М на n шагах, а функцию можно разложить
по формуле Тейлора до членов порядка  :
:
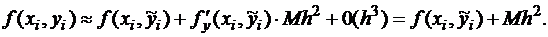
На примере метода Эйлера нужно обратить внимание еще на одну закономерность, которая прослеживается и в других методах – зависимость точности результата от величины шага h. Вычисляя y1, мы полагали, что значение y0 определено точно, но исходные данные x0, y0 бывают найдены из некоторых дополнительных измерений и допускают определенную ошибку, назовем ее α, тогда значение производной
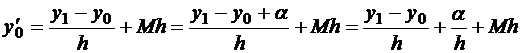 .
.
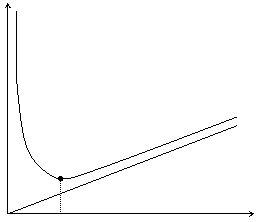
И ошибка при вычислении производной имеет вид: 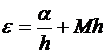 . Рассмотрим эту зависимость графически. Это гипербола, нас интересует положительная ветвь.
. Рассмотрим эту зависимость графически. Это гипербола, нас интересует положительная ветвь.
Для сравнительно больших значений шага h погрешность убывает
с уменьшением шага, но если продолжать уменьшать шаг меньше некоторого критического значения 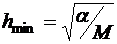 , то погрешность начинает резко расти. Таким образом,
, то погрешность начинает резко расти. Таким образом, 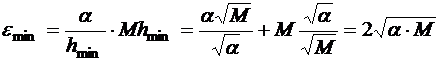 .
.
Вывод прост и понятен: никакая вычислительная наука не позволит вам получить результат существенно точнее, чем те исходные данные, которые вы используете. Если же вы настаиваете и уменьшаете шаг вычислений
и дальше, то получаете далекие от точного решения численные результаты. Этот вывод справедлив и для других численных методов.
|
|
|
Рис. 1.1. Уравнение асимптоты 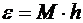
Современная наука предложила много других методов для решения задачи Коши. Но метод Эйлера не потерял своей актуальности благодаря простоте использования, хотя, он дает хорошее приближение только для малых h и первых 3-4 шагов. Недостатками метода Эйлера является малая точность
и систематическое накопление ошибок.
Задача Коши для обыкновенных дифференциальных
уравнений 1-го порядка. Методы Рунге-Кутта
Методы Рунге-Кутта – одношаговые методы, существенно более точные, чем метод Эйлера.
Общая схема получения методов. Идея методов Рунге-Кутта состоит
в том, что, в отличие от метода Эйлера, приближенное значение на следующем шаге вычисляется вначале в некоторых промежуточных точках, а затем усредняется:
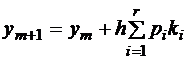 , (1.3)
, (1.3)
где 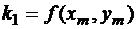 – из метода Эйлера,
– из метода Эйлера, 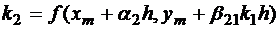 ,
,
. . . . . . . . . . . . . . .
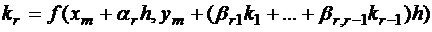 ,
,
r ≥ 1 – фиксированное целое число, порядок точности метода, pi, αi, βij – параметры. Эти параметры определяются при конкретных значениях r из того, чтобы погрешность метода на шаге была наименьшей по порядку. Определим эти параметры для r=2. Из формулы (1.3) получаем
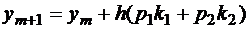 , (1.4)
, (1.4)
где 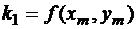 ,
, 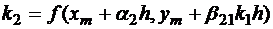 .
.
Для определения параметров оценим погрешность метода на шаге Δm(h). 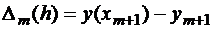 , где
, где 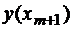 – точное значение в точке xm+1, ym+1 – приближенное значение, вычисленное по формуле (1.4), исходя из точного
– точное значение в точке xm+1, ym+1 – приближенное значение, вычисленное по формуле (1.4), исходя из точного 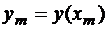 . Запишем разложение функции по формуле Тейлора:
. Запишем разложение функции по формуле Тейлора:
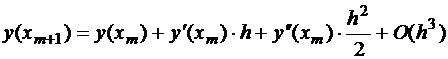 . (1.5)
. (1.5)
Из дифференциального уравнения 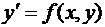 , которое запишем, как
, которое запишем, как 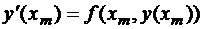 и продифференцируем:
и продифференцируем:
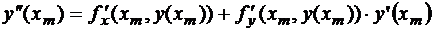 или
или
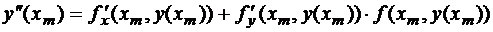 .
.
Из формулы (1.5)
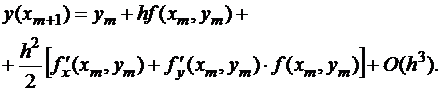 (1.6)
(1.6)
Из формулы (1.4)
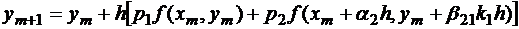 .
.
Из формулы Тейлора для двух переменных:

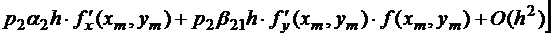 ,
,
т.к. 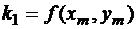 ,
, 
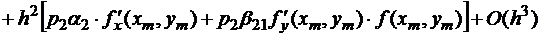 . (1.7)
. (1.7)
Из сравнения формул (1.4) и (1.5) получаем систему уравнений
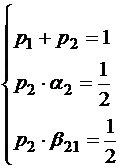 (1.8)
(1.8)
В системе три уравнения и четыре неизвестных. Такая система имеет бесконечно много решений. Одно из неизвестных может быть выбрано произвольно. Чаще всего встречаются следующие два частных решения.
I. 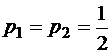 ,
, 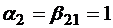 ;
;
II. 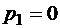
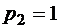 ,
, 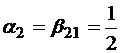 .
.
В I случае расчетная формула метода Рунге-Кутта 2-го порядка имеет вид:
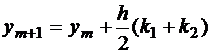 , где из формулы (1.4)
, где из формулы (1.4) 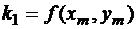 ;
;
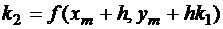 .
.
Во II случае вычисления проводятся по схеме
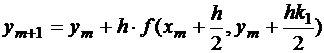 , где
, где 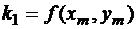 .
.
Система (1.8) получается из условия наиболее полного возможного совпадения формул (1.6) и (1.7) и обеспечивает равенство слагаемых – свободных, линейных и квадратных в этих формулах, таким образом, погрешность полученных методов на шаге имеет порядок точности 3: 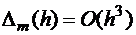 . Полная погрешность метода на всем интервале [a;b] за n шагов составляет величину
. Полная погрешность метода на всем интервале [a;b] за n шагов составляет величину 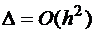 .
.
Основной метод Рунге-Кутта получается при r=4. Вывод формул аналогичен только что рассмотренному, но в формуле Тейлора потребуется продолжить разложение вплоть до слагаемых 4-го порядка. Можно получить
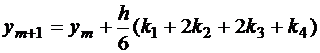 , где
, где 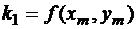 ;
;
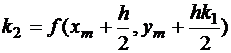 ;
;
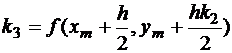 ;
;
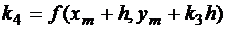 .
.
Погрешность метода на шаге составляет величину 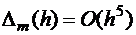 , общая погрешность метода –
, общая погрешность метода – 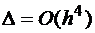 .
.
Формулы погрешности, полученные для методов Рунге-Кутта, позволяют определить порядок метода, т.е. насколько быстро меняется погрешность при изменении шага вычислений, но не дают возможности оценить саму величину погрешности. К.Рунге предложил практическое правило для оценки величины погрешности в случае, если задан порядок метода. Оценка осуществляется двойным пересчетом.
Предположим, вы решаете задачу методом, порядок точности которого равен k, т.е. разница между точным решением y и приближенным решением, полученным с шагом h – yh,,выражается так: 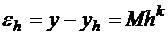 , тогда, если повторить решение той же задачи, но с шагом
, тогда, если повторить решение той же задачи, но с шагом 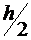 , вы получите более точное решение
, вы получите более точное решение 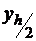 , причем
, причем 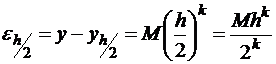
Рассмотрим абсолютную величину разности между точным и приближенным решением для шага  и для шага
и для шага 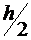 и вычтем уравнения почленно:
и вычтем уравнения почленно:
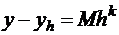 ;
; 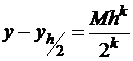 ; получим
; получим 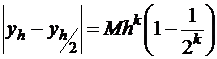 . Преобразуем это выражение к виду:
. Преобразуем это выражение к виду: 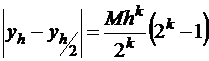 или
или 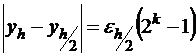 , тогда
, тогда 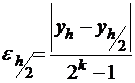 , т.е. погрешность второго пересчета можно оценить. Некоторая условность полученной оценки происходит от того, что в формулах для
, т.е. погрешность второго пересчета можно оценить. Некоторая условность полученной оценки происходит от того, что в формулах для 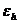 и
и 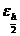 могут оказаться различные константы М. Но лучшего способа оценки погрешности придумано не было.
могут оказаться различные константы М. Но лучшего способа оценки погрешности придумано не было.
В случае метода Рунге-Кутта четвертого порядка точности 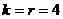
и оценить погрешность можно следующим образом:
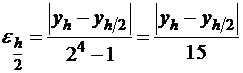 .
.
Отсюда получается правило регулировки шага вычислений. Если вычисленная таким способом 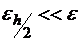 , где ε – наперед заданная предельно допустимая погрешность вычислений, то шаг удваивается, а если
, где ε – наперед заданная предельно допустимая погрешность вычислений, то шаг удваивается, а если 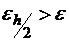 , то шаг измельчается.
, то шаг измельчается.
Краевые задачи для обыкновенного дифференциального
уравнения 2-го порядка
Постановка задачи. На отрезке [a, b] требуется найти решение уравнения 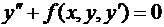 , удовлетворяющее краевым условиям
, удовлетворяющее краевым условиям
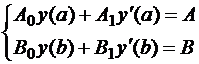 .
.
Пример: 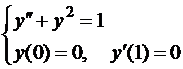 .
.
Вопрос о разрешимости краевой задачи не имеет универсального ответа не только в общем случае, но даже для линейных уравнений.
Пример:
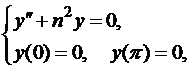
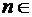 N.
N.
Эта задача имеет для каждого фиксированного  два решения: y=0
два решения: y=0
и y=sin nx. Можно привести пример краевой задачи для линейного уравнения, не имеющей решения.
Вопрос о разрешимости краевой задачи для нелинейного дифференциального уравнения открыт до сих пор. Для линейных дифференциальных уравнений этот вопрос решен:
1) однородная задача 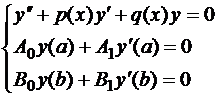
имеет не более конечного числа линейно-независимых решений;
2) неоднородная задача 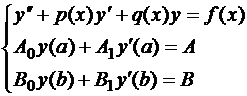
разрешима тогда и только тогда, когда f(x), A, B удовлетворяют конечному числу условий ортогональности.
В дальнейшем будем предполагать, что решение краевой задачи существует и единственно.
Существует несколько способов решения краевых задач. Рассмотрим конечно-разностный или сеточный способ.
Разобьем промежуток [a; b] на n частей узловыми точками xi=a+ih,
где 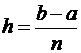 – шаг вычислений, yi=y(xi). Построим конечно-разностную аппроксимацию неоднородной задачи:
– шаг вычислений, yi=y(xi). Построим конечно-разностную аппроксимацию неоднородной задачи:
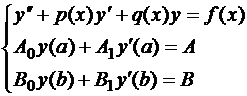 . (1.9)
. (1.9)
с краевыми условиями:
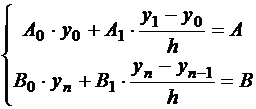 ;
;
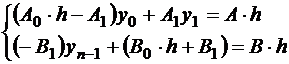 . (1.10)
. (1.10)
Введем обозначения b0=A0·h-A1, c0=A1, d0=Ah, an=-B1, bn=B0·h +B1, dn=Bh, тогдауравнения запишутся:
b0y0+c0y1=d0 ;
anyn-1+bnyn=dn .
Для основного уравнения применим аппроксимацию
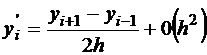 ;
; 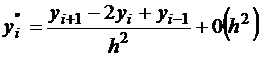 ; тогда пренебрегая слагаемыми второго порядка при подстановке в уравнение, получим:
; тогда пренебрегая слагаемыми второго порядка при подстановке в уравнение, получим:
 .
.
Будем считать, что pi=p(xi), qi=q(xi), fi=f(xi), тогда получим:
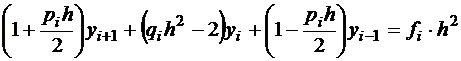 , обозначим
, обозначим
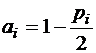 ,
, 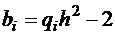 ,
, 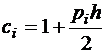 ,
, 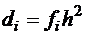 .
.
Разностная аппроксимация для основного уравнения запишется так 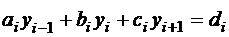 . Индекс i меняется от 0 до n, но при i=0
. Индекс i меняется от 0 до n, но при i=0
не определено i-1, а при i=n не определено i+1, значит, основное уравнение имеет смысл только при i=1,2,3…, n-1. Таким образом, получено n-1 уравнение, вместе с двумя уравнениями аппроксимации краевых условий получится система из n+1 уравнения, содержащая n+1 неизвестное: y0,y1…, yn.Решив эту систему, можно найти приближенные значения функции y=y(x) в узловых точках, т.е. получить сеточное решение краевой задачи (1.9)-(1.10).
Системы линейных алгебраических уравнений решают разными способами: по правилу Крамера, матричным методом через обратную матрицу, разложением матрицы на произведение двух треугольных, но самым рациональным является метод Гаусса, он требует наименьшего объема вычислений. Система, которую требуется решить, особенная – в каждом уравнении не более трех переменных. Для таких систем в 50-х гг. прошлого века советские математики предложили упрощенную схему метода Гаусса – метод прогонки.
Запишем всю систему уравнений
 b0y0+c0y1 =d0;
b0y0+c0y1 =d0;
a1y0+b1y1+c1y2 =d1;
a2y1+b2y2+c2y3= d2;
. . .
an-1yn-2+bn-1yn-1+cn-1yn=dn-1;
anyn-1+byn =dn.
Матрица такой системы состоит в основном из нулей, ненулевые элементы расположены только на главной диагонали и на двух линиях вдоль нее:
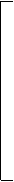
 b0 c0 . . . . . . . .
b0 c0 . . . . . . . .
a1 b1 c1 . . . . . .
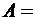 . a2 b2 c2 . . . . . . . .
. a2 b2 c2 . . . . . . . .
 . . . . . . . .
. . . . . . . .
.. . . an-1 bn-1 cn-1
. . . . . . an bn
Такие матрицы называются ленточными, или трехдиагональными. Именно для систем с такими матрицами и разработан метод прогонки. Как
и метод Гаусса, он состоит из двух этапов – прямого хода и обратного хода.
Прямой ход.Из первого уравнения выразим y0 :
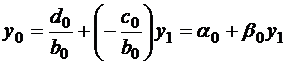 , где
, где 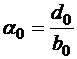 ;
; 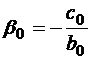 .
.
Подставим это выражение y0 во второе уравнение:
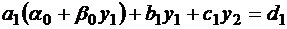 , теперь оно содержит две неизвестных, выразим y1
, теперь оно содержит две неизвестных, выразим y1
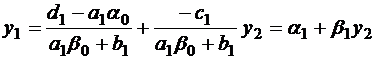 ,
,
где 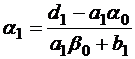 ;
; 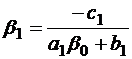 .
.
Подставим выражение для y1 в следующее уравнение:
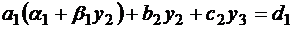 и выразим из него y2
и выразим из него y2
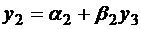 , где
, где 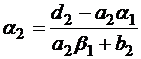 ;
; 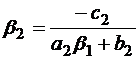 .
.
Таким образом, можно выразить 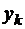 :
:
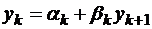 , где
, где 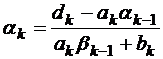 ;
; 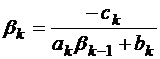 .
.
Продолжим вычислять значения 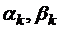 пока не дойдем до последнего уравнения:
пока не дойдем до последнего уравнения: 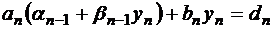 , в этом уравнении всего одна неизвестная, найдем ее значение:
, в этом уравнении всего одна неизвестная, найдем ее значение: 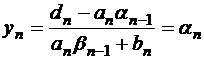 .
.
Обратный ход.Зная yn, можно найти 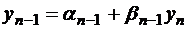 . Зная
. Зная 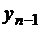 , можно найти
, можно найти 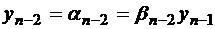 . С каждым шагом узнаем значение новой переменной, номер которой на 1 меньше предыдущей. Так добираемся до y0. Все переменные найдены, задача решена.
. С каждым шагом узнаем значение новой переменной, номер которой на 1 меньше предыдущей. Так добираемся до y0. Все переменные найдены, задача решена.
Метод прогонки решения краевых задач является методом второго порядка точности. Основное достоинство метода – устойчивость. При оценке погрешности следует применять правило двойного пересчета Рунге.
Дата добавления: 2018-05-12; просмотров: 2376; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
