Метод Галеркина для обыкновенных дифференциальных уравнений 2-го порядка

⇐ ПредыдущаяСтр 3 из 17Следующая ⇒

В начале XX в. в Санкт-Петербурге известными механиками, сначала И.Г.Бубновым, а затем (1915) Б.Г.Галеркиным был предложен метод решения однородных краевых задач для дифференциальных уравнений, называемый также методом моментов, – метод нахождения приближенного решения дифференциального уравнения в виде линейной комбинации элементов заданной линейно независимой системы функций.

Рассмотрим краевую задачу

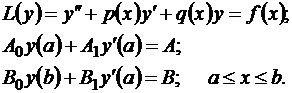
Эту краевую задачу легко можно свести к однородной с помощью замены 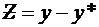, где функция y* удовлетворяет краевым условиям, например, 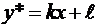, где

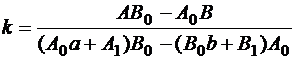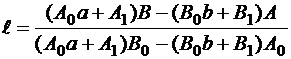Таким образом, не уменьшая общности, можно считать краевую задачу однородной

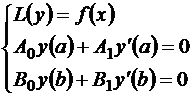
Будем искать приближенное решение этой краевой задачи в виде

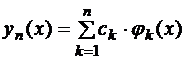Система функций φ₁(x), φ₂(x)… φ_n(x) называется базисной, или координатной системой.

Рассмотрим скалярные произведения левой и правой частей основного уравнения на базисные функции. Скалярным произведением двух функций называется интеграл от их произведения

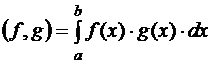Если 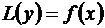, то .

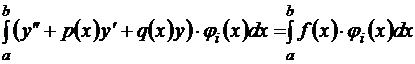Получившееся уравнение называется моментным, или проекционным, его можно расписать подробнее, учитывая, что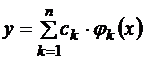

;

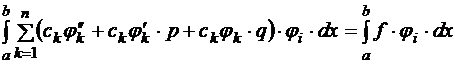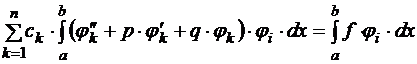Обозначим 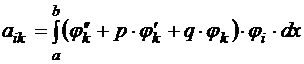, , 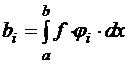тогда система моментных уравнений примет вид: 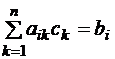для i=1, 2,…,n.

Запишем систему в привычном виде:

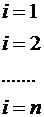
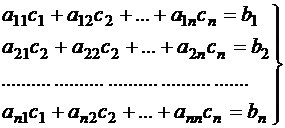Это система линейных алгебраических уравнений, число неизвестных совпадает с числом уравнений. Если такую систему решить, можно найти коэффициенты c₁, c₂, …, c_n и записать ответ, приближенное решение однородной краевой задачи .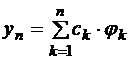

При решении краевой задачи методом Галеркина можно выделить три основных этапа:

1) выбор базисной системы φ₁(x), φ₂(x), …;

2) численное решение моментных уравнений;

3) предельный переход при n→∞.

В практических задачах ограничиваются конечным числом базисных функций, т.е. следует рассмотреть только первые два этапа. Будем считать, что с решением системы линейных уравнений трудностей не возникает. Исследуем подробнее пункт 1. Теоретически имеем: для любых однородных краевых условий

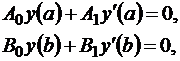
всегда можно найти базисную систему функций, удовлетворяющих этим краевым условиям. Однако на практике выбор этой системы может представить значительные затруднения. Чаще в базис входит две – три базисные функции, которые выбирают из следующих соображений: φ₁(x) имитирует предполагаемое поведение ответа, а φ₂(x) и φ₃(x) – невязки. Однако имеются и некоторые общие способы выбора таких базисных систем. Рассмотрим два таких случая:

1) специальный базис;

2) кусочно-линейный базис (метод конечных элементов).

Случай 1. Выбор специального базиса связан с понятием собственных элементов (собственных функций) дифференциальных уравнений. Допустим, что краевые условия таковы, что дифференциальный оператор 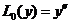, действующий на функцию y(x), удовлетворяющую этим условиям, есть самосопряженный оператор, т.е. скалярное произведение (y'', φ)= (y, φ'') для любых функций y(x), φ(x), удовлетворяющих краевым условиям. Самосопряженный оператор имеет чисто точечный спектр, т.е. существует конечная система собственных чисел λ₁, λ₂, …, λ_n и соответствующая система собственных функций φ₁, φ₂, …, φ_n, таких что 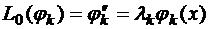, где 1 ≤ k ≤ n.

Система 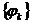образует ортогональный базис в L₂ на (a; b). Эту систему и принимают за базисную систему в методе Галеркина.

Примеры:

1) 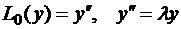, y(a)=0, y(b)=0. Ищем решение, удовлетворяющее этим условиям – первая краевая задача:

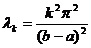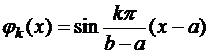, , k=1, 2, …, n;

2) 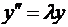, y'(a)=0, y'(b)=0, ;

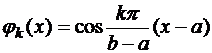3) 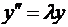, y(a)=0 ,y'(b)=0, .

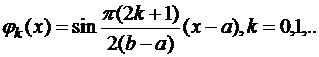Приближения y_n(x) в методе Галеркина могут обладать следующей особенностью: несмотря на то, что теоретически y_n(x)→ y(x) при n→∞, может случиться, что y₃(x) дает лучшее приближение, чем y₄(x), …, y₇(x) и лишь y₈(x) лучшее, чем y₃(x). Это связано с тем, что сходимость y_n(x) не является монотонной. Имеются необходимые и достаточные условия монотонной сходимости. В частности, система, образующая ортогональный базис, условиям минимальности, обеспечивающим монотонность, удовлетворяет.

Случай 2. Метод конечных элементов. Применительно к краевой задаче для обыкновенных дифференциальных уравнений метод конечных элементов есть метод Галеркина при специально выбранном кусочно-линейном базисе.

Уравнение 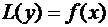можно привести к дивергентной форме:

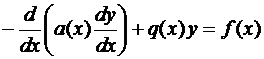для этого умножим исходное уравнение на функцию –a(x): 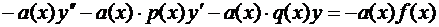, при этом функцию a(x) выбираем так, чтобы a'(x)=a(x)∙p(x), т.е.

, ;

, , .

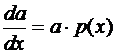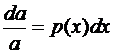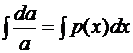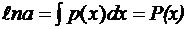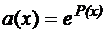При таком выборе a(x) уравнение можно записать иначе:

;

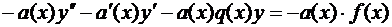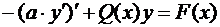,где ;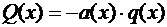

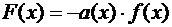Это и есть дивергентная форма записи дифференциального уравнения.

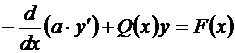Будем считать, что дифференциальное уравнение изначально задано в таком виде: –(a∙y')'+q(x)y=f(x); (1.9)

а краевые условия

y(a₀)=0, y(b₀)=0; (1.10)

где a(x), q(x) непрерывны на [a₀,b₀], в частности, если a(x) и q(x)≥0, то решение задачи (1.9), (1.10) существует и единственно.

Выбор базиса. Разобьем [a₀,b₀] на n частей с шагом h, a₀=x₀< x₁<…<x_n=b₀, тогда

ω₂^k(x)

ω₁^k(x)

x_k+1

x₀

x₁

x_n

x_k-1

x_k

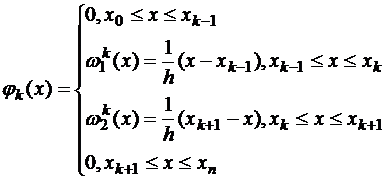
Рис. 1.2. График базисных функций

В соответствии с методом Галеркина положим

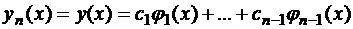– кусочно-линейная функция, имеющая, быть может, изломы только в точках x₀, x₁, …, x_n: y(x_k)=y_k=c_k при k=1, 2, …, n-1; y(x₀)=y(x_n)=0 – граничные условия выполнены. Для определения y_k выпишем моментные уравнения Галеркина:

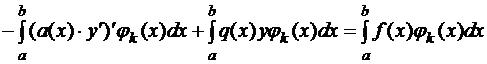, k=1, 2, …, n-1.

В силу выбора 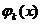интегрирование идет по интервалу [x_k_-1, x_k₊₁].

Имеем

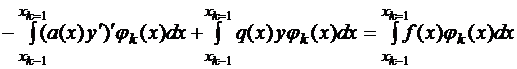(1.11)

Первое слагаемое интегрируем по частям

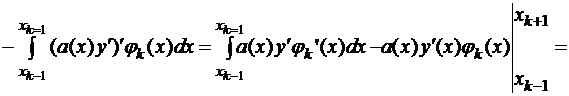
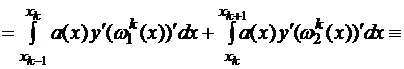
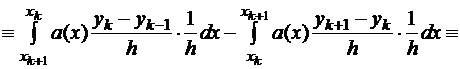
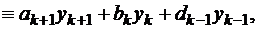
где

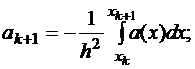
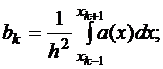
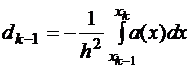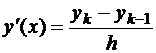на интервале [x_k_-1, x_k], т.к. 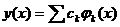– кусочно-линейная функция, ломаная.

Аналогично 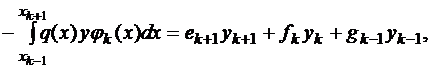где

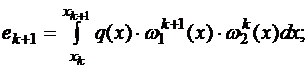
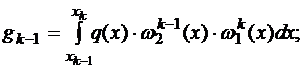
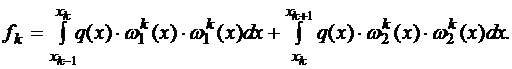
Обозначим 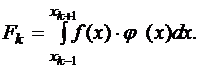Подставляя найденные выражения в формулу (1.11), получаем

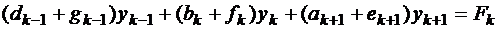, где k=1, , n-1. Это трехдиагональная система, которую можно решить методом прогонки. Таким образом, значения y_k найдены, задача приближенно решена.

Для нахождения коэффициентов трехдиагональной системы требуется взять большое количество интегралов. Немного позже будут рассмотрены способы приближенного вычисления определенных интегралов.

Аппроксимация функций

Дата добавления: 2018-05-12; просмотров: 2275; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 234 5 6 7 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!