Численные методы решения обыкновенных дифференциальных уравнений
Федеральное агентство по образованию
Дальневосточный государственный технический университет
(ДВПИ им. В.В. Куйбышева)
А.А. Бочарова, Е.П. Луппова, А.А. Ратников
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
Учебно-методический комплекс
Рекомендовано Дальневосточным региональным учебно-методическим
центром в качестве учебного пособия для студентов вузов региона
Издательство
ДВГТУ
| |
УДК 681.3.06+519.6
ББК 32.973я73
Б72
Рецензенты:
Г.К. Пак, канд. физ.-мат. наук, профессор
(Дальневосточный государственный университет);
А.Ю. Чеботарев, д-р физ.-мат. наук, профессор
(Институт прикладной математики ДВО РАН)
Бочарова, А.А.
Б Вычислительная математика: учеб. метод. комплекс /А.А. Бочарова; Е.П. Луппова; А.А. Ратников; Под ред. А.А. Бочаровой; Дальневосточный государственный технический университет. – Владивосток: Изд-во ДВГТУ, 2008. – с.
ISBN 978-5-7596-0923-0
Учебно-методический комплекс «Вычислительная математика» предназначен для студентов второго курса инженерно-технических специальностей.
Конспект лекций содержит основные сведения по разделам: численные методы линейной алгебры, решения обыкновенных дифференциальных уравнений и краевых задач, аппроксимация функций, методы интегрирования, сеточные методы. Практикум включает примеры решения типовых заданий, выполненных в математическом пакете Mathcad, которые могут быть использованы студентами для самостоятельной работы.
|
|
|
УДК 681.3.06+519.6
ББК 32.973я73
| ISBN 978-5-7596-0923-0 | © Дальневосточный государственный технический университет, 2008 |
Оглавление
1. Численные методы решения обыкновенных дифференциальных уравнений……………………………………………………………………………1
Основные понятия…………………………………………………………………...1
Элементы теории погрешностей……………………………………………………2
Численное дифференцирование. Аппроксимационные формулы………………3
Задача Коши для обыкновенного дифференциального
уравнения 1-го порядка. Метод Эйлера……………………………………………9
Задача Коши для обыкновенных дифференциальных
уравнений 1-го порядка. Методы Рунге-Кутта…………………………………...13
Краевые задачи для обыкновенного дифференциального
уравнения 2-го порядка……………………………………………………………17
Метод Галеркина для обыкновенных дифференциальных уравнений 2-го порядка…………………………………………………………………………...…22
2. Аппроксимация функций……………………………………………………..30
Интерполяционный многочлен Лагранжа………………………………………..30
Многочлены Чебышева…………………………………………………………….35
|
|
|
Минимизация погрешности интерполяции полинома
Лагранжа………………………………………………………………………….…37
Интерполяция с равноотстоящими узлами……………………………………….39
Кусочная аппроксимация…………………………………………………………..40
Сплайн-интерполяция……………………………………………………………...41
Метод наименьших квадратов…………………………………………………….43
Ортогональные полиномы…………………………………………………………48
3. Численное интегрирование…………………………………………………...51
Простейшие квадратурные формулы……………………………………………..51
Квадратурные формулы Ньютона-Котеса………………………………………..55
Экстраполяция по Ричардсону…………………………………………………….57
Квадратурные формулы Гаусса, Чебышева………………………………………57
Метод Монте-Карло………………………………………………………………..63
4. Уравнения в частных производных…………………………………………65
5. Численные методы линейной алгебры……………………………………...73
Матрицы и действия над ними…………………………………………………….73
Клеточные матрицы……………………………………………………………..…80
Разложение матрицы на произведение двух треугольных матриц……………...83
|
|
|
Итерационные методы……………………………………………………………..88
Метод Якоби………………………………………………………………………..94
Метод Зейделя………………………………………………………………..96
Введение
Вычислительная математика является одной из основных дисциплин, входящих в учебный план подготовки специалистов в области информатики
и компьютерной техники.
Предмет изучения вычислительной математики – методы решения и исследования математических задач, которые чаще всего не могут быть решены точно, аналитически. Такие задачи решают численно – приближенно с некоторой погрешностью.
Математика осваивает технологии приближенных вычислений в течение нескольких веков, и за это время был сформирован математический аппарат численного решения алгебраических уравнений, обыкновенных дифференциальных уравнений, уравнений математической физики, численного дифференцирования и интегрирования. Первые результаты в этом направлении связаны с именами Л. Эйлера, И. Ньютона, но современные численные методы были предложены совсем недавно, в конце XX века.
Изучение курса вычислительной математики предполагает не только освоение теоретических основ методов, но и изучение возможностей, которые предоставляют исследователю современные вычислительные средства. Для работы с математическими пакетами достаточно знания основных идей и понимания особенностей в применении численных методов, чтобы решить научную или инженерную задачу, провести сравнительный анализ результатов.
|
|
|
Практикум по вычислительной математике содержит решения основных типовых заданий в пакете MathCad, предлагаемые студенту для самостоятельной работы, а также краткое описание и примеры решений некоторых задач в системе аналитических вычислений Maple.
Численные методы решения обыкновенных дифференциальных уравнений
Основные понятия
В вычислительной математике рассматривается не только вопрос, как решить некоторый тип задач, но и как оценить погрешность, возникающую при его решении. Насколько отличается приближенное решение от точного решения той же самой задачи? Будет ли разница между точным и приближенным решениями стремиться нулю при продолжении и уточнении вычислительного процесса, т.е. будет ли численный метод сходящимся?
В технике очень часто исходные данные, используемые для решения задачи, бывают получены опытным путем, т.е. в них изначально присутствует некоторая погрешность эксперимента. Как повлияет эта погрешность начальных данных на точность конечного результата, на точность решения? Численные методы, обеспечивающие малую погрешность результата при малой ошибке в исходных данных, называются устойчивыми.
Сходимость и устойчивость являются главными достоинствами вычислительной схемы, но также очень важна скорость сходимости. Для того чтобы её оценить, стараются получить конкретную зависимость погрешности результата вычислений от параметров вычислений, обычно в виде 
, где М – некоторая постоянная, неизвестная при вычислениях, h – шаг вычислений – параметр, выбираемый исследователем самостоятельно. Тогда постоянная k называется порядком точности метода. Чем выше порядок k, тем легче, уменьшая шаг h, добиться уменьшения погрешности.
Для того чтобы вычислитель имел возможность выбрать из множества методов тот, который наиболее пригоден для решения конкретной задачи, ему требуется знание основ численного моделирования.
Элементы теории погрешностей
При численном решении задачи неизбежно появление погрешности следующих трех типов:
погрешность задачи,
погрешность метода решения,
погрешность вычислений.
Погрешность задачи складывается из погрешности математической модели и погрешности начальных данных. Математическая формулировка задачи должна описывать основные законы процесса. Выбор математической модели требует глубокого понимания сущности явления. Погрешность, возникающая из-за несоответствия выбранной математической модели реальному процессу, как и погрешность, связанная с неточностью данных, входящих в описание задачи, является неустранимой погрешностью.
Для решения математических задач используются аналитические
и численные методы. При использовании аналитических методов решение задачи можно представить в виде формул, в которые начальные данные могут входить в виде параметров. Для решения сложных задач чаще используются численные методы, которые позволяют свести решение задачи к выполнению конечного числа арифметических действий над числами. Численные методы позволяют получить решение задачи при конкретных начальных значениях.
Погрешность метода возникает в результате замены исходной математической задачи более простой вычислительной, например, решение дифференциального уравнения заменяется разностным уравнением.
В курсе вычислительной математики изучается, как можно сделать погрешность метода сколь угодно малой.
Погрешность вычислений или погрешность округлений возникает вследствие того, что компьютер работает с приближенными, усеченными
до количества разрядов, значениями действительных чисел.
Различают два вида погрешностей – абсолютную и относительную.
Абсолютная погрешность числа равна разности между его истинным значением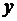 
и приближенным 
, полученным в результате измерения
или вычисления:
.
Относительная погрешность равна отношению абсолютной погрешности к приближенному значению числа.
.
Обычно точное значение числа неизвестно, поэтому находят предельную погрешность, являющуюся верхней оценкой модуля 
и ее принимают в качестве абсолютной погрешности приближенного числа , тогда как истинное значение 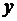находится в интервале 
.
Для приближенного числа, полученного в результате округления, абсолютная погрешность 
принимается равной половине единицы последнего разряда числа. Например,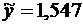 
, 
; 
.
Приведенные оценки погрешностей приближенных чисел справедливы, если в записи этих чисел все значащие цифры верные. Значащимися цифрами считаются все цифры данного числа, начиная с первой ненулевой. Например, в числе 0,053 значащие цифры – 5 и 3, в числе 15,30 все четыре значащие.
Значащая цифра называется верной, если модуль погрешности числа
не превосходит единицы разряда, соответствующего этой цифре. Например,
, следовательно, все четыре значащие цифры – верные; если 
, следовательно, пять значащих цифр – верные.
На практике используют правило, согласно которому приближенное число должно записываться так, чтобы в нем все значащие цифры, кроме последней, были верными и лишь последняя была бы сомнительной в среднем не более, чем на одну единицу, т. е. предполагается, что в самой записи приближенного числа содержится информация о его точности.
Чтобы результаты арифметических действий, совершаемых над приближенными числами, также соответствовали этому принципу, следует
во всех промежуточных вычислениях сохранять на одну-две значащих цифры больше, чем это оправдывается точностью исходных данных или метода. Запасные значащие цифры затем должны быть отброшены.
Дата добавления: 2018-05-12; просмотров: 746; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!