Решение систем линейных уравнений матричным способом
Рассмотрим квадратную систему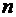 
линейных уравнений с 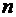неизвестными:
(5.1)
Определим основную матрицу системы 
, как матрицу, образованную из коэффициентов при неизвестных, матрицу-столбец 
и матрицу- столбец неизвестных 
:
, 
, 
.
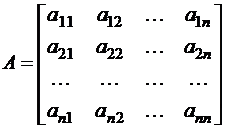Всякую систему линейных уравнений (5.1) можно записать в матричном виде:
.
Если – матричное уравнение с квадратной матрицей, определитель которой не равен нулю, тогда решение можно найти в виде
.
Всякая система линейных уравнений с определителем основной матрицы, не равным нулю, имеет единственное решение.
На практике эффективность решения системы (5.1) зависит от свойств матрицы . Например, при большой размерности системы использование формул Крамера для нахождения неизвестных становится труднореализуемым, т. к. для вычисления определителя порядка 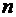требуется 
умножений. Факториальный рост количества арифметических операций с увеличением размерности задачи – очень быстрый рост – называют “проклятием размерности”. По тем же причинам обращение матрицы через алгебраические дополнения практически непригодно.
Рассмотрим для начала прямые методы решения систем, которые достаточно просты и универсальны. Существенным недостатком прямых методов является накапливание погрешностей в процессе вычислений, которые на любом этапе используют результаты предыдущих операций.
При использовании итерационных методов погрешности не накапливаются, т. к. точность вычислений в каждой итерации определяется лишь результатами предыдущей итерации и практически не зависит от ранее выполненных вычислений. Итерационные методы предпочтительнее в случае большого числа уравнений и плохо обусловленных систем.
|
|
|
Системы уравнений называются плохо обусловленными, если малые погрешности вычислений или исходных данных могут привести к существенным погрешностям в решении, например, когда определитель системы близок к нулю.
Норма матрицы
Под нормой матрицы понимается некоторое действительное число 
. Матрица: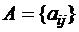 
определяется тремя нормами:
1) 
максимальная сумма модулей элементов по строкам;
2) 
максимальная сумма модулей элементов по столбцам;
3) 
корень из суммы квадратов всех элементов.
Иногда 
, здесь 
– собственные числа матрицы .
Пример. Найти нормы матрицы : 
,
, 
, 
.
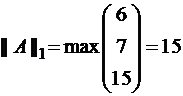Свойства нормы:
1) 
, причем норма равна нулю только для нулевой матрицы;
2) 
;
3) 
;
4) 
.
Аналогично наиболее употребительные нормы для векторов 
:
1) 
;
2) 
;
3) 
.
Клеточные матрицы
При вычислениях с матрицами большой размерности удобно разбить их на клетки с помощью вертикальных и горизонтальных линий-разделителей и с полученными матрицами меньших размеров работать.
|
|
|
.
Над клеточными матрицами можно производить операции сложения и умножения, работая с клетками матрицы как с элементами обычной матрицы.
Рассмотрим 
, 
, где 
– матрицы одного и того же типа и разбиения, тогда их сумма и произведение будет:
; 
.
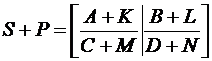Можно разбить матрицу 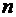-ого порядка на клетки так называемым окаймлением, т. е. выделяем матрицу размерности (n – 1), последние строку, столбец и матрицу первого порядка – 
:
.
Действия над окаймленными матрицами проводят также, как действия над клеточными матрицами.
Дата добавления: 2018-05-12; просмотров: 442; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!