Интерполяция с равноотстоящими узлами
Рассмотрим систему равноотстоящих узлов интерполяции:
.
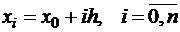Будем обозначать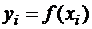 
, введем переменные:
,
.
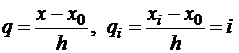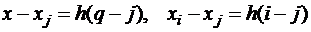Рассмотрим интерполяционный полином Лагранжа первого порядка:
,
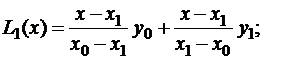
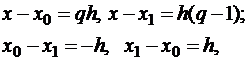тогда получим:
.
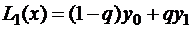Аналогично для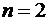 
:
.
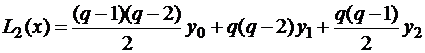В общем случае:
.
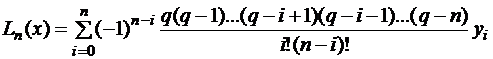Поскольку при оценке погрешности интерполяционного полинома Лагранжа используется функция
,
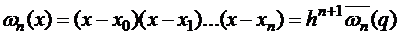где
,
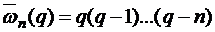то погрешность полинома Лагранжа с равноотстоящими узлами интерполяции равна
.
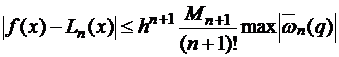При этом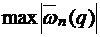 
не зависит от 
, следовательно, ее величину можно оценить для любого 
. На практике редко используют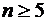 
. Функция 
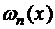имеет большие значения ближе к концам промежутка интерполяции 
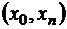, поэтому узлы выбирают так, чтобы нужная точка находилась ближе к середине интервала.
Кусочная аппроксимация
Кусочная аппроксимация – способ приближения таблично заданных функций с помощью составных звеньев, которые являются полиномами невысокой степени, допускающими гладкую стыковку.
Рассмотрим аппроксимацию кусочно-линейной функцией.
Пусть заданы точки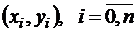 
. Будем требовать, чтобы ломаная проходила через точки
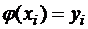. (2.5)
Будем строить функцию в виде:
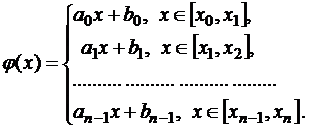
Для нахождения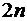 
неизвестных коэффициентов получим систем уравнений из условий (2.5):
.
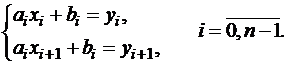Кусочно-квадратичная аппроксимация при четном числе отрезков интерполяции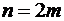 
имеет вид:
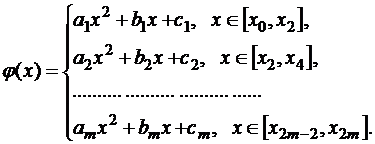
Каждая тройка коэффициентов 
может быть найдена последовательным решением систем линейных уравнений третьего порядка вида:
|
|
|
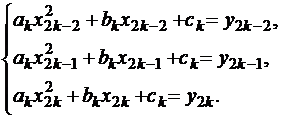
Сплайн- интерполяция
Сплайном называется функция, которая является многочленом на каждом частичном отрезке интерполяции, а на всем отрезке непрерывна вместе с несколькими своими производными.
Пусть отрезок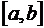 
разбит на частей,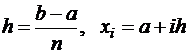 
.
Максимальная по всем частичным отрезкам интерполяции степень многочлена называется степенью сплайна.
Разность между степенью сплайна и порядком наивысшей непрерывной на 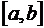производной называется дефектом сплайна. Например, ломаная- непрерывная кусочно-линейная функция – это сплайн первой степени с дефектом единица. Чаще всего используются кубические сплайны 
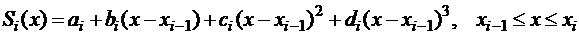. (2.6)
Для определения коэффициентов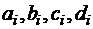 
на всех отрезках интерполяции требуется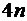 
уравнений. Часть из них можно получить из условий:
,
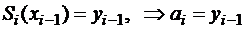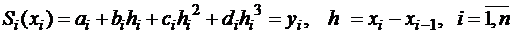. (2.7)
В этой системе всего 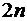уравнений. Для получения недостающих условий зададим условия непрерывности первой и второй производных во внутренних узлах интерполяции, т. е. условия гладкости второго порядка кривой во всех точках:
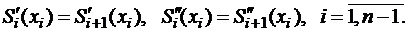(2.8)
Вычислим производные многочлена (2.6):
,
,
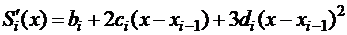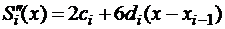тогда из условий (2.8) получим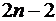 
уравнений:
|
|
|
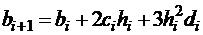; (2.9)
, 
.
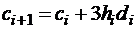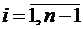Чтобы получить дополнительные условия, накладывают требования к поведению сплайна на концах отрезка интерполяции, из условия нулевой кривизны на концах следуют равенства нулю вторых производных в этих точках:
.
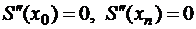Приведем систему уравнений к более удобному виду. Поскольку все коэффициенты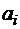 
уже известны, выразим
.
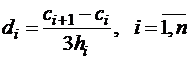Подставим эти соотношения и значения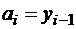 
в уравнение (2.7) и выразим оттуда коэффициенты:
.
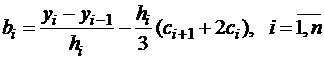Исключив из уравнения (2.9) коэффициенты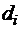 
и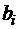 
, окончательно получим систему уравнений только для коэффициентов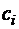 
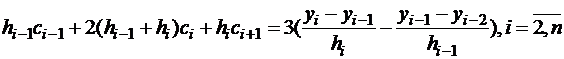, (2.10)
.
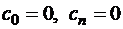Здесь введен фиктивный коэффициент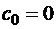 
. Данная система (2.10) имеет единственное решение, т. к. выполняется условие диагонального преобладания в матрице, следовательно, существует единственный кубический сплайн дефекта единицы. Для решения системы целесообразно использовать метод прогонки. По найденным из системы коэффициентам 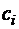легко вычислить коэффициенты 
.
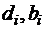Метод наименьших квадратов
Если набор точек 
получен из эксперимента с некоторой погрешностью, то не имеет смысла использовать интерполяцию полиномами Лагранжа или сплайнами для обработки результатов.
|
|
|
В этом случае необходимо провести аппроксимирующую кривую, которая не проходит через экспериментальные точки, но в то же время отражает исследуемую зависимость, сглаживая возможные выбросы за счет погрешности эксперимента.
Будем рассматривать непрерывную функцию 
, аппроксимирующую дискретную зависимость 
. Подберем функцию так, чтобы сумма квадратов отклонений во всех точках была бы минимальной:
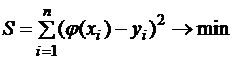(2.11)
Метод построения аппроксимирующей функции из условия минимума S называется метод наименьших квадратов.
Наиболее распространен выбор в виде обобщенного полинома:
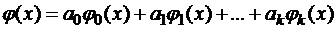, (2.12)
где 
– базисные функции. Формула для определения суммы квадратов отклонений будет иметь вид:
.
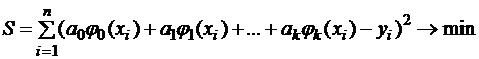Продифференцируем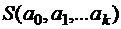 
по переменным и приравняем производные нулю:
, 
;
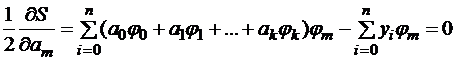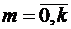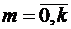, . (2.13)
Здесь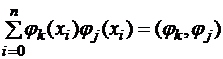 
– скалярное произведение дискретных функций. Таким образом, получили систему 
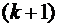линейных уравнений (2.13) относительно неизвестных 
.
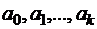Основная матрица системы – матрица Грама составлена из попарных скалярных произведений дискретных функций:
.
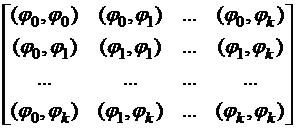Аналогично определим скалярное произведение дискретной функции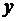 
: 
.
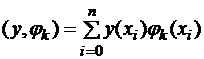Матрица Грама симметричная, положительно определённая, ее определитель не равен нулю, если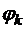 
– линейно независимые.
|
|
|
Обычно начинают с одной или двух базисных функций, если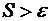 
, где 
– погрешность экспериментальных данных, то добавляют новые 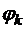, пока 
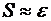. Выбор конкретных базисных функций зависит от свойств 
– периодичности, логарифмического или экспоненциального характера.
Нередко для исследователя требуется не только аппроксимирующая функция, но и ее производные, которые можно найти дифференцированием аппроксимирующей функции:
.
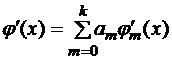Аналогично можно найти производные второго и более высоких порядков.
Степенной базис
Выберем в качестве базисных функций степенные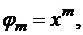 
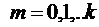, тогда 
.
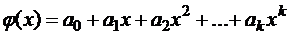В этом случае, как и при интерполяции, аппроксимируем экспериментальную зависимость полиномом, однако здесь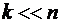 
, обычно 
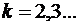. При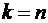 
получим интерполирующий полином Лагранжа.
В случае степенного базиса система (2.13) примет вид:
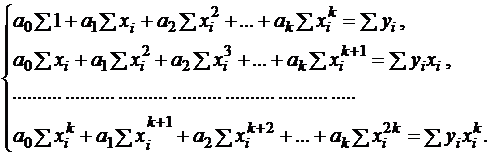
Для формирования расширенной матрицы достаточно вычислить только элементы первой строки и двух последних столбцов, остальные элементы можно заполнить присвоением. Здесь предполагается суммирование под знаком суммы по всем 
от 0 до .
Если порядок аппроксимирующего полинома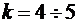 
, то можно решать систему методом Гаусса, если 
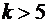, то разработан метод сингулярного разложения решений такой системы уравнений.
Частный случай линейной аппроксимации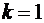 
, 
,
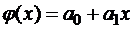для нахождений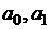 
требуется решить систему уравнений:
.
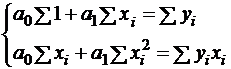Для квадратичной аппроксимации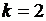 
, 
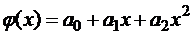, следует решить систему следующего вида:
.
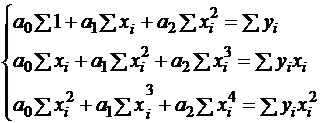Для наилучшего выбора аналитической зависимости следует рассмотреть несколько вариантов и выбрать тот, которому соответствует наименьшее значение суммы квадратов отклонений. В практикуме показано, что, используя возможности вычислительного пакета MathCad, можно в качестве аппроксимирующей функции выбирать разные зависимости вида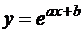 
, 
, 
.
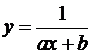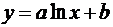Дата добавления: 2018-05-12; просмотров: 2090; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!