Обращение матриц разбиением на клетки
Задача решения линейной неоднородной системы уравнений и задача обращения матрицы тесно связаны друг с другом. Если требуется решить систему  , и для матрицы
, и для матрицы  известна обратная матрица
известна обратная матрица 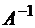 , то получим
, то получим 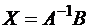 . Рассмотрим обращение клеточных матриц.
. Рассмотрим обращение клеточных матриц.
Пусть  – клеточная матрица размерности
– клеточная матрица размерности 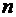 , в которой матрицы
, в которой матрицы 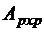 и
и 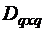 – квадратные, причем
– квадратные, причем 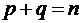 . Найдем обратную матрицу
. Найдем обратную матрицу 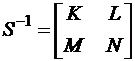 , в которой матрицы
, в которой матрицы 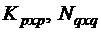 также квадратные.
также квадратные.
По определению 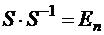 , где единичная матрица также клеточная, в которой
, где единичная матрица также клеточная, в которой 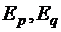 – единичные матрицы соответствующих порядков
– единичные матрицы соответствующих порядков
 .
.
Перемножив матрицы и приравняв соответствующие элементы,
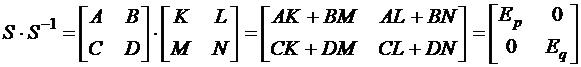 ,
,
получим:
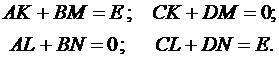
Полагаем, что 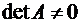 , т.е. существует обратная матрица
, т.е. существует обратная матрица 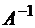 , тогда
, тогда
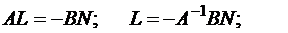
 ;
;
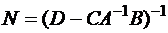 ;
; 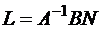 ;
;
 ;
; 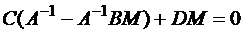 ;
;
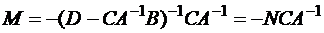 .
.
Таким образом, если вычисления начинаются с  , то используем следующие формулы:
, то используем следующие формулы:
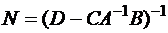 ;
;
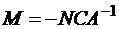 ;
;
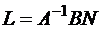 ;
;
 .
.
Вторая группа формул используется если обращение начинается с  :
:
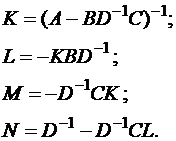 .
.
В практикуме разобран пример решения системы четвертого порядка в пакете Mathcad.
Разложение матрицы на произведение двух треугольных матриц
Матрица называется нижней треугольной, если элементы, стоящие выше ее главной диагонали, равны нулю: если 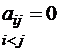 :
:
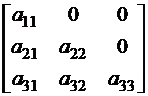 ,
,  .
.
Матрица называется верхней треугольной, если элементы, стоящие ниже ее главной диагонали, равны нулю: 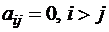 .
.
Определитель треугольной матрицы равен произведению ее диагональных элементов 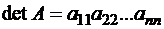 .
.
Обратная матрица неособенной треугольной матрицы также треугольная матрица того же ранга и структуры. Матрица, обратная к левой треугольной, является левой треугольной, обратная к правой – правой треугольной.
Например, возьмем нижнюю треугольную матрицу:
 ,
, 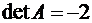 .
.
Выпишем алгебраические дополнения элементов:
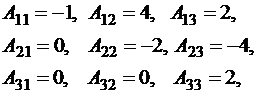
тогда обратная матрица будет:
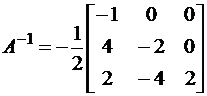 ,
,
т. е. 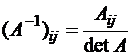 – алгебраические дополнения ненулевых элементов строго нижней треугольной матрицы равны нулю:
– алгебраические дополнения ненулевых элементов строго нижней треугольной матрицы равны нулю:
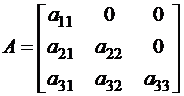 ;
;  .
.
Теорема. Если квадратная матрица  имеет отличные от нуля главные миноры
имеет отличные от нуля главные миноры 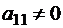 ,
, 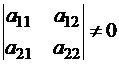 ,…,
,…, 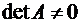 и т. д., то ее можно разложить на произведение двух треугольных матриц (верхней и нижней). Это разложение будет единственным, если задать диагональные элементы одной из матриц отличными от нуля, например, положить их равными единице.
и т. д., то ее можно разложить на произведение двух треугольных матриц (верхней и нижней). Это разложение будет единственным, если задать диагональные элементы одной из матриц отличными от нуля, например, положить их равными единице.
Пусть  , будем рассматривать вывод формул на примере матриц четвертого порядка:
, будем рассматривать вывод формул на примере матриц четвертого порядка:
 ;
; 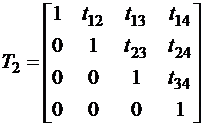 .
.
Перемножаем матрицы:
 ,
,
приравниваем соответствующие элементы матриц 
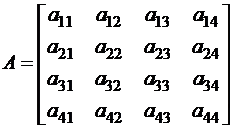 .
.
Последовательно решая одночленные, двучленные и т.д. уравнения получим
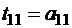 ,
, 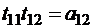 ,
, 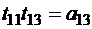 ,
, 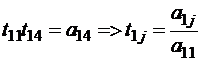 ;
;
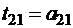 ,
, 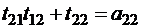 ;
;
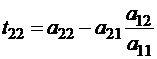 , …
, …  ;
;

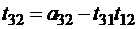 ,
, 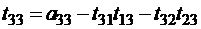 ;
;
 .
.
Таким образом, для матриц порядка 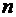 , получим формулы общего вида:
, получим формулы общего вида:
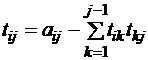 ,
, 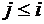 – элементы матрицы
– элементы матрицы 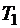 ;
;
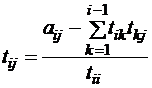 ,
, 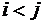 – элементы матрицы
– элементы матрицы  .
.
Такое разложение матриц на две треугольные называется LU – разложение (от английского left – right).
При практическом разложении нужно иметь в виду, что поскольку в формулах для матрицы 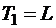 выполняется деление на диагональные элементы
выполняется деление на диагональные элементы 
 , то удобнее делать проверку на равенство нулю этих элементов, вместо проверки на равенство нулю главных миноров.
, то удобнее делать проверку на равенство нулю этих элементов, вместо проверки на равенство нулю главных миноров.
Отметим, что для матриц с диагональным преобладанием, для которых верно
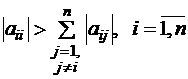 ,
,
условия теоремы о LU – разложении заведомо выполняются.
Обратим матрицу, которая представлена произведением двух треугольных: 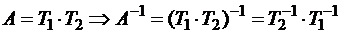 ;
; 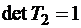 ;
;
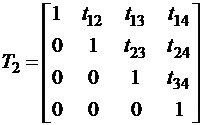 ;
; 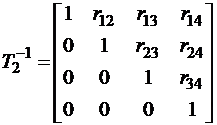 ;
;
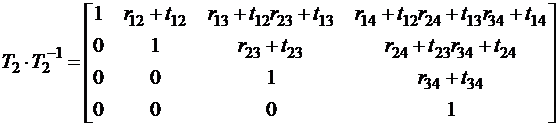 .
.
Приравнивая элементы произведения соответствующим элементам единичной матрицы  , получим
, получим
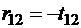 ,
, 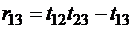 ,
, 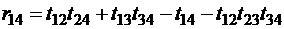 ;
;
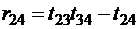 ,
, 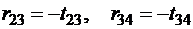 .
.
Аналогично обращается матрица  .
.
Дата добавления: 2018-05-12; просмотров: 1488; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
