Решение СЛАУ с помощью LU – разложения
Если матрица исходной системы уравнений
 (5.2)
(5.2)
разложена на произведение двух треугольных матриц  или
или  , значит можно записать эквивалентное уравнение
, значит можно записать эквивалентное уравнение
 .
.
Введем в рассмотрение матрицу-столбец промежуточных неизвестных:
 ,
,
тогда решение системы с исходной матрицей (5.2) сводится к решению системы двух матричных уравнений:

каждое из которых имеет треугольную матрицу. Решая последовательно вначале систему  , находим
, находим  – вектор вспомогательных переменных, затем решаем систему
– вектор вспомогательных переменных, затем решаем систему  и находим
и находим  , как если бы выполняли обратный ход метода Гаусса.
, как если бы выполняли обратный ход метода Гаусса.
Получим формулы для вспомогательных неизвестных  :
:
 ,
,  ,
,
 ,
,  ;
;
 ,
, 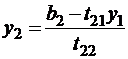 ;
;
 . (5.3)
. (5.3)
Решаем систему  , получим:
, получим:
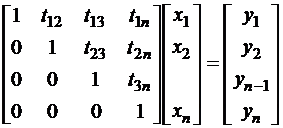 ; (5.4)
; (5.4)



 . (5.5)
. (5.5)
Отметим, что выполнение расчетов по формулам (5.3,5.5) представляет собой преобразование системы (5.2) к треугольной системе (5.4), которая полностью совпадает с результатом прямого хода метода Гаусса. Таким образом, решение линейных систем с помощью LU-разложения является просто другой реализацией метода Гаусса. Схему LU-разложения еще называют схемой Холецкого (1875-1918 – французский математик-геодезист). Однако в применяемых математических пакетах, таких как MathCad, схемой Холецкого называют метод решения систем с симметричной матрицей (метод квадратного корня).
При решении систем линейных алгебраических уравнений прямыми методами с использованием компьютера происходит подмена арифметики действительных чисел машинной арифметикой, т. е. действия совершаются с усеченными до определенного количества разрядов числами. Практически всегда вместо точного решения СЛАУ прямой метод дает приближенное решение –  . Рассмотрим разность
. Рассмотрим разность
|
|
|
 ,
,
где  – вектор невязок. По малости полученных невязок или нормы вектора
– вектор невязок. По малости полученных невязок или нормы вектора  можно судить о близости в некотором смысле найденного решения
можно судить о близости в некотором смысле найденного решения  к точному решению
к точному решению  .
.
Итерационные методы
Итерационные методы решения систем линейных алгебраических уравнений предпочтительнее прямых в случае систем большой размерности.
Рассмотрим метод простой итерации. Пусть требуется решить систему
 . (5.6)
. (5.6)
Прежде чем применять метод итерации систему (5.6) следует привести к равносильной системе вида
 . (5.7)
. (5.7)
Здесь  – некоторые новые матрицы. Итерационный процесс состоит в том, что последовательно исправляются значения неизвестных. Решение системы получается как предел некоторой единым образом построенной последовательности приближений.
– некоторые новые матрицы. Итерационный процесс состоит в том, что последовательно исправляются значения неизвестных. Решение системы получается как предел некоторой единым образом построенной последовательности приближений.
|
|
|
Пусть нам известно некоторое начальное приближение  ( о его выборе скажем позже). Подставим
( о его выборе скажем позже). Подставим  в правую часть равенства (5.7), получим следующее приближение:
в правую часть равенства (5.7), получим следующее приближение:
 ,
,
затем поступим с  аналогично, получим
аналогично, получим  и так далее:
и так далее:
 ;
;
 . (5.8)
. (5.8)
Таким образом строится последовательность матриц -столбцов  .
.
Если последовательность матриц-столбцов  сходится к решению системы
сходится к решению системы  , то говорят, что метод итерации для данной системы сходится.
, то говорят, что метод итерации для данной системы сходится.
Можно доказать, что если последовательность  имеет предел
имеет предел  , то этот предел является решением системы (5.7), а следовательно, и (5.6). Если формально в равенстве (5.8) перейти к пределу при
, то этот предел является решением системы (5.7), а следовательно, и (5.6). Если формально в равенстве (5.8) перейти к пределу при  , то т. к.
, то т. к. 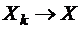 , то равенство (5.8) примет вид
, то равенство (5.8) примет вид  , т. е. предел
, т. е. предел  является решением системы (5.7). Выясним условия, при которых последовательность
является решением системы (5.7). Выясним условия, при которых последовательность  имеет предел.
имеет предел.
Рассмотрим последовательность решений системы (5.7)

Получается в скобках сумма конечного числа матриц:
 ,
,
при  получим матричный ряд
получим матричный ряд
 . (5.9)
. (5.9)
Лемма. Для того, чтобы  необходимо и достаточно, чтобы все собственные числа матрицы
необходимо и достаточно, чтобы все собственные числа матрицы  были бы по модулю меньше единицы:
были бы по модулю меньше единицы: 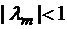
 .
.
Допустим, что все собственные числа матрицы  различны, тогда существует невырожденная матрица
различны, тогда существует невырожденная матрица  , такая, что
, такая, что  , где
, где  – диагональная матрица
– диагональная матрица
|
|
|
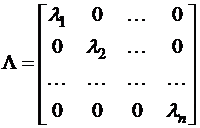 ,
,
тогда матрица  может быть преобразована к диагональному виду:
может быть преобразована к диагональному виду:
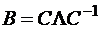 .
.
Возведем в степень обе части по правилам действия с матрицами
 ;
;
 .
.
Здесь
 .
.
Для того, чтобы  , необходимо и достаточно, чтобы
, необходимо и достаточно, чтобы  , а для этого необходимо и достаточно, чтобы
, а для этого необходимо и достаточно, чтобы 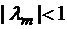
 .
.
На практике легче вычислить норму матрицы, чем решать задачу о нахождении собственных значений, поэтому удобнее использовать следующую теорему, дающую достаточные условия.
Теорема.Для того, чтобы  , достаточно, чтобы какая-нибудь из норм матрицы
, достаточно, чтобы какая-нибудь из норм матрицы  была меньше единицы.
была меньше единицы.
На основании свойств нормы можно записать  . Т. к.
. Т. к.  , это и означает, что
, это и означает, что  .
.
Верно утверждение о том, что модуль каждого собственного числа матрицы не превосходит любой из ее норм  .
.
Теорема.Для того, чтобы ряд  сходился, необходимо и достаточно, чтобы
сходился, необходимо и достаточно, чтобы  , при этом сумма ряда равна
, при этом сумма ряда равна  .
.
Необходимость условия очевидна. Докажем достаточность. Пусть  , следовательно,
, следовательно, 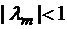
 , значит, нет ни одного собственного числа, равного единице, тогда
, значит, нет ни одного собственного числа, равного единице, тогда  и существует обратная матрица
и существует обратная матрица  . Обозначим сумму сходящегося ряда
. Обозначим сумму сходящегося ряда
 .
.
Рассмотрим выражение:
|
|
|
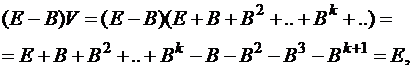
тогда
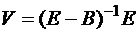 ,
,  .
.
Теорема. Необходимое и достаточное условие сходимости метода итераций.Для того, чтобы метод простых итераций сходился при любом начальном векторе  , необходимо и достаточно, чтобы все собственные значения матрицы
, необходимо и достаточно, чтобы все собственные значения матрицы  были бы по модулю меньше единицы.
были бы по модулю меньше единицы.
Необходимость. Пусть  , тогда
, тогда  является решением системы (5.7), следовательно,
является решением системы (5.7), следовательно,
 ,
,  .
.
Вычтем из первого равенства второе, получим:
 .
.
К разности  можно применить аналогичные рассуждения:
можно применить аналогичные рассуждения:
 ,
,
т. к.  , то
, то  , поскольку
, поскольку  – произвольный вектор, то
– произвольный вектор, то  ,
,  , следовательно, все собственные числа матрицы
, следовательно, все собственные числа матрицы  по модулю меньше единицы.
по модулю меньше единицы.
Достаточность. Пусть  . Перейдем в равенстве
. Перейдем в равенстве

к пределу при  , тогда
, тогда  ,
,  , следовательно
, следовательно 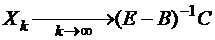 , а это решение системы (5.7), а значит и системы (5.6).
, а это решение системы (5.7), а значит и системы (5.6).
Проверить выполнение условий доказанной теоремы довольно трудно. Для практического применения метода итераций нужно иметь достаточные условия , которые даются в следующей теореме.
Теорема. Для того, чтобы метод простых итераций сходился при любом начальном векторе  к единственному решению
к единственному решению  , достаточно, чтобы какая-нибудь норма матрицы
, достаточно, чтобы какая-нибудь норма матрицы  была меньше единицы
была меньше единицы  , при этом справедливы оценки погрешности:
, при этом справедливы оценки погрешности:
 – апостериорная;
– апостериорная;
 – априорная.
– априорная.
Априорная оценка, как правило, грубее апостериорной.
Априорная оценка позволяет подсчитать заранее число итераций, достаточное для получения  с заданной точностью
с заданной точностью  при выбранном начальном векторе
при выбранном начальном векторе  . Для этого нужно найти наименьшее целое решение неравенства
. Для этого нужно найти наименьшее целое решение неравенства

относительно  :
:  , т. к.
, т. к.  ,
,  .
.
Апостериорной оценкой удобно пользоваться непосредственно в процессе вычислений и останавливать этот процесс, как только выполнится неравенство  .
.
Отметим, что неравенство 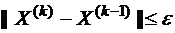 будет гарантией того, что
будет гарантией того, что  только, если
только, если 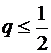 .
.
Обычно за  принимают вектор
принимают вектор  – матрицу-столбец свободных членов системы (5.7), если неизвестно какое-нибудь близкое решение. Если
– матрицу-столбец свободных членов системы (5.7), если неизвестно какое-нибудь близкое решение. Если 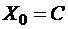 , то априорная оценка имеет вид:
, то априорная оценка имеет вид:
 – при любом
– при любом  .
.
Дополнительно отметим, что процесс итераций сходится, если все элементы  , где
, где  – число неизвестных.
– число неизвестных.
Метод Якоби
Чтобы решить систему
 (5.10)
(5.10)
методом простой итерации, необходимо привести ее к виду
 . (5.11)
. (5.11)
После того, как мы выяснили, каким условиям должна удовлетворять матрица  для сходимости метода, следует выяснить как привести систему (5.10) к виду (5.11), чтобы это условие сходимости выполнялось.
для сходимости метода, следует выяснить как привести систему (5.10) к виду (5.11), чтобы это условие сходимости выполнялось.
Представим матрицу  системы (5.10) в виде:
системы (5.10) в виде:
 ,
,
где  – диагональная,
– диагональная,  и
и  – левая и правая строго треугольные (т.е. с нулевой диагональю) матрицы. Тогда система (5.10) может быть записана в виде:
– левая и правая строго треугольные (т.е. с нулевой диагональю) матрицы. Тогда система (5.10) может быть записана в виде:
 .
.
Если на диагонали исходной матрицы нет нулей, то эквивалентной (5.10) задачей вида (5.11) будет
 , (5.12)
, (5.12)
т. е.
 ,
,  .
.
Метод простых итераций, основанный на таком приведении системы (5.10) к виду (5.11), называется метод Якоби . Тогда последовательность приближений по методу простой итерации имеет вид:
 .
.
Здесь  – обратная к матрице
– обратная к матрице  – диагональная матрица
– диагональная матрица
 ,
,  ,
,
поэтому представление системы в виде (5.12) равнозначно выражению диагональных неизвестных:
 ;
;
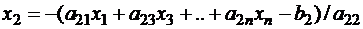 ;
;
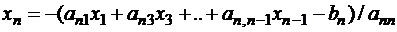 .
.
Теперь для записи итерационного процесса в развернутом виде следует расставить номера итераций:
 ;
;
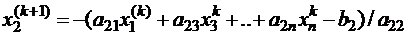 ; (5.13)
; (5.13)
 .
.
Достаточный признак сходимости метода Якоби к решению системы (5.10) сформулирован в следующей теореме.
Теорема. В случае диагонального преобладания в матрице  системы (5.10) метод Якоби (5.13) сходится.
системы (5.10) метод Якоби (5.13) сходится.
Диагональное преобладание означает, что: 
 .
.
Тогда в матрице 
 ,
,
сумма модулей элементов в любой строке меньше единицы  , следовательно, одна из норм (по крайне мере одна) матрицы
, следовательно, одна из норм (по крайне мере одна) матрицы  меньше единицы, т. е. метод Якоби сходится.
меньше единицы, т. е. метод Якоби сходится.
Метод Зейделя
Под методом Зейделя понимают такое видоизменение метода простых итераций (5.12) решения систем линейных уравнений, приведенных к виду (5.11), при котором при подсчете i-ой компоненты  приближения к искомому
приближения к искомому  используются уже найденные на этом
используются уже найденные на этом  шаге новые значения первых
шаге новые значения первых  компонент, т. е. приближения к решению системы (5.11) по методу Зейделя определяются выражениями:
компонент, т. е. приближения к решению системы (5.11) по методу Зейделя определяются выражениями:
 .
.
Здесь  ,
,  - компоненты начального приближения
- компоненты начального приближения  . Эти формулы можно записать в виде:
. Эти формулы можно записать в виде:
 ;
; 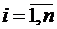 .
.
Если приведение СЛАУ (1) к виду (5.11) основано на представлении (5.12), то метод Зейделя есть модифицированный метод Якоби:
 .
.
Для метода Зейделя

Теорема. Если  , то при любом
, то при любом  метод Зейделя сходится к точному решению системы
метод Зейделя сходится к точному решению системы  и справедливы оценки погрешности:
и справедливы оценки погрешности:
 .
.
Если матрица  имеет диагональное преобладание, то метод Зейделя сходится быстрее, чем метод Якоби.
имеет диагональное преобладание, то метод Зейделя сходится быстрее, чем метод Якоби.
Пример. Решить систему методом итерации:

Приведем систему к нормальному виду:
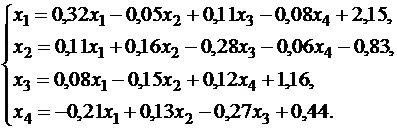
Здесь 
 . Вычислим норму матрицы
. Вычислим норму матрицы 

 , следовательно, метод простых итераций сходится.
, следовательно, метод простых итераций сходится.
Пусть 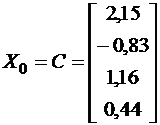 ,
,  ;
;
 ;
;  ;
;  – оценка числа итераций.
– оценка числа итераций.
Дата добавления: 2018-05-12; просмотров: 1812; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
