Цепь с резистором и катушкой индуктивности

Цепь переменного тока с этими двумя элементами, включен­ными последовательно, показана на рисунке 4.6, а.

Напряжение, приложенное к катушке, состоит из двух слагаемых: из падения напряжения в активном сопро­тивлении U_a = Ir и индуктивном сопротивлении U_l = I ∙ x_L.

Так как вектор падения напряжения U_a совпадает по направлению с вектором тока, а вектор U_L опережает его на 90°, то, сложив геометрически оба вектора, по­лучаем вектор напряжения U (рисунок 4.6, б). Таким обра­зом, в цепи с реальной катушкой ток тоже отстает от напряжения, но на угол φ, меньший 90°.

Треугольник АОВ называется треугольником напряже­ний цепи переменного тока, содержащей активное и ин­дуктивное сопротивления.

Из треугольника напряжений вытекают следующие соотношения:

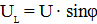
Проекция вектора напряжения на вектор тока называется активной составляющей вектора напряжения и обозначается U_a, а проекция вектора напряжения на направление, перпендикулярное вектору тока, называется реактивной составляющей вектора напряжения и обозначается U_p. По аналогии вектор тока может быть разложен на активную и реактивную составляющие:

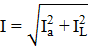
Рисунок 4.7 - Электрическая цепь с резистором, катушкой индуктивности и конденсатором: а) - схема; б) - векторная диаграмма напряжений и тока

Если стороны треугольника напряжений разделить на ток I то получим треугольник сопротивлений (рисунок 4.6, в), катетами которого являются активное r и индуктивное x_L сопротивления, а гипотенузой  -  величина z = , называемая полным сопротивлением цепи.

Ток цепи определяется по закону Ома:

Угол сдвига фаз между током и напряжением опре­деляется из векторных диаграмм (рисунок  4.6, б, в):

или

4.7 Цепь с резистором, катушкой индуктивности и кон­денсатором

На рисунке  4.7 а,представлена электрическая цепь переменного тока, обладающая активным сопротив­лением (резистор), индуктивностью (катушка) и емкостью (конденсатор).

В такой цепи действующее значение приложенного напряжения состоит из трех составляющих: активной U_а, индуктивной U_L и емкостной U_C: U = U_а + U_L + U_C (суммирование производится геометрически, рисунок  4.7, б).

Отдельные составляющие действующих значений на­пряжения:

Из векторной диаграммы видно, что активное падение напряжения U_а совпадает с током, индуктивное U_L опережает ток на 90°, а емкостное U_C отстает от тока на 90°.

Из треугольника напряжений ОАС следует, что напряжение, приложенное к цепи:

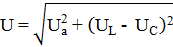
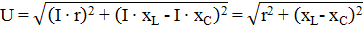
Отсюда ток:

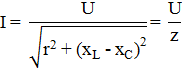
Эта формула выражает закон Ома применительно кнеразветвленной цепи переменного тока.

Сдвиг по фазе между напряжением и током определит­ся выражением:

Сопротивление цепи, определяемое формулой:

Называется полным сопротивлением цепи. Сопротивление x = x_L -  x_C   называется реактивным.

Возможны следующие случаи соотношений x_L и x_C:

· x_L > x_C тогда φ > 0, в цепи преобладает индуктив­ность;

· x_L < x_C, тогда  φ < 0, в цепи преобладает емкость;

· x_L = x_C, или ω ∙ L = l/ω ∙ C, тогда φ = 0, соs φ = 1.

Сопротивление цепи минимальное, ток достигает при этом наибольшего возможного значения. Напряжения на зажи­мах катушки и конденсатора могут превосходить напря­жение на зажимах цепи в десятки раз. Поэтому резонанс при последовательном соединении элементов называют резонансом напряжений. Резонанс напряжений может воз­никнуть только при небольших активных сопротивлениях цепи. Режим резонанса напряжений в технике сильных токов является аварийным, так как при этом изоляция катушек конденсаторов может быть пробита. В высоко­частотной технике (радиотехнике) резонанс напряжений является нормальным режимом и используется для уси­ления напряжений.

При угловой частоте ш подведенного напряжения ре­зонанс напряжений можно получить путем изменения емкости С или индуктивности цепи L так, чтобы ω ∙ L = 1/ω ∙ С, или при постоянных L и С цепи  -  путем из­менения частоты подведенного напряжения.

Угловая частота собственных колебаний в контуре ω_о = 1/  или частота f = 1/2 ∙ π ∙ , т. е. ω_о ∙ L = 1/ ω ∙ С. Следовательно, явление резонанса имеет место при равен­стве частот колебательного контура и источника перемен­ного тока ω_о = ω. Угловая частота ω_о, при которой на­ступает резонанс, называется резонансной угловой часто той цепи и зависит только от величины индуктивности и емкости цепи.

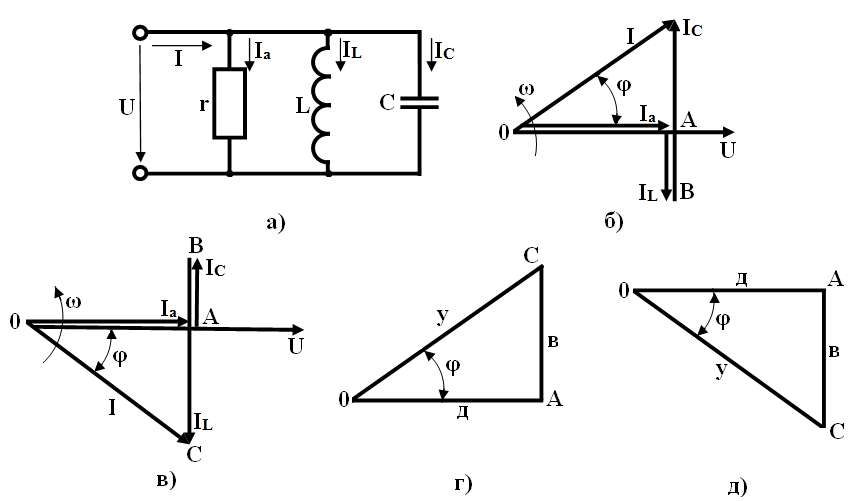
Рисунок 4.8 - Электрическая цепь с параллельным соединением резистора, катушки индуктивности и конденсатора: а) - схема; б) и в) - векторные диаграммы напряжения и токов; г)ид) - треугольники проводимостей

При резонансе напряжений энергия магнитного поля W_м = L ∙ I₂/2 равна энергии электрического поля W_э = C ∙ U₂/2 и передается от катушки к конденсатору и обратно при колебаниях тока и напряжения без потребления энергии от источника. Возникают незатухающие колебания. Обмен энергией между катушкой и конденсатором совершается через источник энергии, который восполняет потери энергии в активных сопротивлениях.

4.8 Параллельное соединение резистора, катушки индук­тивности и конденсатора

В такой цепи (рисунок  4.8, а) дей­ствующее значение тока в неразветвленной части цепи состоит из трех слагаемых: активной I_а, индуктивной I_L и емкостной I_С:

(суммирование произво­дится геометрически).

Возможны следующие случаи соотношений I_C и I_L: ток I_C > I_L тогда φ < 0, ток в неразветвленной части цепи опережает напряжение; вектор I_р (отрезок АС), обозначающий реактивную составляющую тока, направлен вверх от вектора напряжения (рисунок  4.8, б); ток I_C  < I_L, тогда φ > 0, ток в неразветвленной части цепи отстает от напряжения, вектор I_р (отрезок АС) направлен вниз от вектора напряжения (рисунок  4.8, в); ток I_C = I_L, тогда φ = 0; соs φ = 1, ток в неразветвленной части цепи совпадает по фазе с напряжением и равен активному току, т. е. I = I_а.

Активная составляющая тока I_а имеет один и тот же знак при любых значениях φ. Реактивная составляющая тока меняет знак вместе с изменением знака угла φ. Разделив каждую из сторон треугольника токов на действующее напряжение U, получим треугольник проводимостей (рисунок  4.8, г, д).

Так как соs φ = r/z, a sin φ = x/z, получим выражения для токов и проводимостей при эквивалентном параллельном соединении:

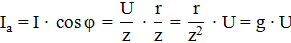
где g =  -  активная проводимость;

b = b_L -  b_c = x_L/z² -  x_C/z² = x/z² -  реактивная проводимость;

y =  =  -  полная проводимость.

Из треугольника проводимостей:

Действующее значение тока в неразветвленной части цепи:

Если разветвленная цепь состоит из соединенных параллельно индуктивности и емкости, то в такой цепи при равенстве ω ∙ L = 1/ω ∙ C возникает явление резонанса токов, при котором токи в ветвях I_L и I_C (рисунок  4.8, а) равны между собой и могут значительно превышать общий ток I, протекающий в неразветвленной части цепи.

Условия появления резонанса токов аналогичны условиям появления резонанса напряжений.

При резонансе токов вся энергия, подводимая к цепи, расходуется на выделение тепла в активном сопротивлении цепи, а между индуктивностью и емкостью происходит колебательный обмен запасенной энергией.

Режим резонанса токов имеет большое практическое значение. Электрические резонансные контуры используются в радиотехнике, измерительной технике, телеуправлении, различных схемах автоматики. Явления резонанса используются также для изменения параметров линий электропередач. Параллельным подключением емкостей к активно-индуктивной нагрузке повышают коэффициенты мощности нагрузки, разгружая электрические сети от пе­ретоков реактивных мощностей.

Мощность, энергия (работа)

В цепях постоянного тока потребляемая мощность определяется как произведение напряжения на силу тока, энергия (работа)  -  как произведение мощности на вре­мя. В цепях переменного тока в большинстве случаев такой простой расчет невозможен.

Если цепь переменного тока содержит только актив­ное сопротивление, без индуктивного и емкостного, то активная мощность определяется как произведение дей­ствующих значений напряжения и тока Р = U ∙ I или Р = I² ∙ r. Эта мощность расходуется в активном сопротив­лении и совершает полезную работу.

Обычно в цепи переменного тока наряду с активным сопротивлением есть еще и индуктивное, а часто и емкостное реактивные сопротивления. В таких цепях имеет место сдвиг фаз между током и напряжением, поэтому активная мощность, развиваемая током, меньше произведения U ∙ I, т. е. Р = U ∙ I cos φ.

Единицами активной мощности, как и мощности по­стоянного тока, являются: ватт (Вт), киловатт (кВт), мегаватт (МВт).

Величина cos φ называется коэффициентом мощности цепи переменного тока. Чем больше этот коэффициент, т. е. чем меньше угол сдвига фаз между током и на­пряжением, тем больше активная мощность цепи при тех же значениях тока и напряжения. Поэтому наиболь­шего значения активная мощность достигает в цепях с чисто активным сопротивлением (φ = 0, соsφ = 1), а в цепях с чисто индуктивным сопротивлением активная мощность равна нулю (φ = 90°, cosφ = 0).

Электрическая энергия W_a, расходуемая в цепи пере­менного тока за время t, определяется как произведение активной мощности на время и является активной энер­гией:

.

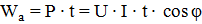
Рисунок 4.9 - Векторная диаграмма мощностей (треугольник мощностей)

Активная энергия измеряется в киловатт-часах (кВт ∙ ч), и ее расход регистрируется счетчиками активной энергии. Цепь переменного тока характеризуется также реактивной Q и полной S мощностью. Реактивная мощность Q = U ∙ I sin φ. Она является мерой скорости обмена энергией между источником тока и потребителем. Не совершая полезной работы, она служит лишь для создания магнитных полей в индуктивных приемниках (электродвигателях, трансформаторах), циркулируя все время между источником тока и приемниками электрической энергии. Единицей измерения реактивной мощности является вольт-ампер реактивный (вар). Более крупная единица - 1 киловольт-ампер реактивный (квар); 1 квар = 10³ вар. Произведение реактивной мощности Q и времени t называется реактивной энергией W ∙ P = Q ∙ t = U ∙ I ∙ t ∙ sin φ.

Реактивная энергия измеряется в киловар-часах (квар ∙ ч). Учет реактивной энергии производится счетчиками реактивной энергии.

Полная мощность S = U ∙ I - это максимально возможная активная мощность при отсутствии сдвига фаз (φ = 0, соs φ = 1). Полная мощность измеряется в вольт-амперах (В ∙ А) или киловольт-амперах (кВ ∙ А). Она является основным параметром, характеризующим генераторы переменного тока и силовые трансформаторы.

Полная, активная и реактивная мощности связаны между собой соотношением:

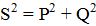
или

Т.е. таким же соотношением, как и стороны прямоугольного треугольника, катеты которого представляют активную и реактивную мощности, а гипотенуза - полную мощность цепи (рисунок  4.9).

Из треугольника мощностей следует, что:

Активная мощность:

Реактивная мощность:

---

Дата добавления: 2018-04-15; просмотров: 9958; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!