Цепь с катушкой индуктивности

В действительности цепей, которые обладали бы только индуктивностью, нет, так как любая катушка обязательно содержит и актив­ное сопротивление. Для уяснения физической стороны процесса рассмотрим катушку, лишенную активного со­противления (рисунок  4.5, в). Примером может служить цепь ненагруженного трансформатора, так как активное со­противление и емкость его незначительны.

Изменение тока в цепи с индуктивностью L вызывает возникновение ЭДС самоиндукции e_L, которая в соответ­ствии с законом Ленца противодействует изменению тока. При увеличении тока ЭДС е_L действует навстречу току.

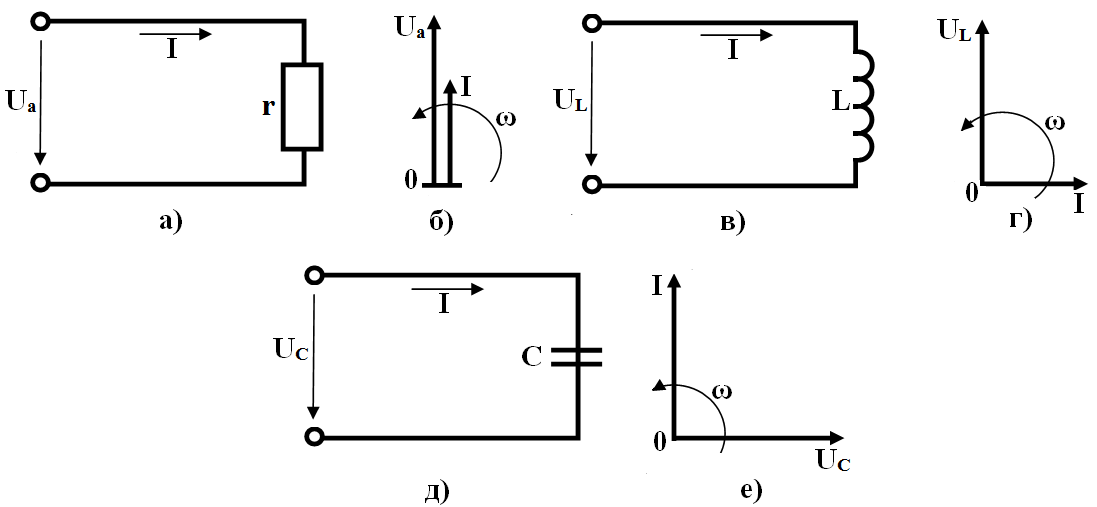
Рисунок 4.5 - Электрические цепи и их векторные диаграммы напряжения и тока: а) и б) - с активным сопротивлением; в) и г) - с катушкой индуктивности; д) и е) - с конденсатором

При уменьшении - в направлении тока, противодей­ствуя его уменьшению:

В дифференциальной форме:

В соответствии с законом Кирхгофа приложенное к цепи напряжение уравновешивается ЭДС самоиндукции u_L = - e_L, следовательно:

где U_Iм = ω ∙ L ∙ I_м -  амплитуда напряжения.

Как видно, фазы у тока и напряжения различны. Напряжение опережает по фазе на π/2 (90°) ток в индуктивности, или ток отстает по фазе на π/2 (90°) от приложенного напряжения (рисунок  4.5, г).

Для действующих напряжения и тока получим выражения, аналогичные по форме закону Ома:

или

Величина ω ∙ L, измеряемая в единицах сопротивления и обозначаемая x_L, называется индуктивным сопротивлением цепи. Индуктивное сопротивление:

пропорционально частоте приложенного напряжения.

Цепь с конденсатором

В цепи с конденсатором (рисунок  4.5, д) емкостью С мгновенный ток равен скорости изменения заряда:

(при условии, что конденсатор не имеет активного сопротивления).

Если напряжение на зажимах конденсатора изменяется по синусоидальному закону:

тоток в цепи:

где I_м = ω ∙ С ∙ U_Cм -  амплитуда тока.

В цепи с емкостью ток опережает по фазе на π/2 (90°) приложенное напряжение (рисунок  4.5, е).

Для действующих значений тока и напряжения получим выражения:

или

Величина 1/ω ∙ С, измеряемая в единицах сопротивления и обозначаемая x_C, называется емкостным сопротивлением цепи. Емкостное сопротивление x_с = 1/(ω ∙ С) = 1/(2 ∙ π ∙ f ∙ C) обратно пропорционально частоте приложенного напряжения.

Примером цепи с емкостью может служить кабельная сеть, так как активное сопротивление и индуктивность этой цепи незначительны.

Рисунок 4.6 -Электрическая цепь с резистором и катушкой индуктивности: а) -  схема; б) -  векторная диаграмма напряжений и тока; в) -  треугольник сопротивлений

Индуктивное и емкостное сопротивления в отличие от активного называются реактивными (неактивными), оказывающими противодействие переменному току элек­трической цепи, но противодействие особое, не связан­ное с преобразованием электрической энергии в тепло­вую. Реактивные сопротивления зависят от частоты при­ложенного напряжения и создают временные сдвиги фаз.

---

Дата добавления: 2018-04-15; просмотров: 1893; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!