Уравнение Ван-дер-Ваальса для одного моля

⇐ ПредыдущаяСтр 10 из 11Следующая ⇒

где р – давление газа, V_m – молярный объем (объем 1-го моля газа), a и b – постоянные Ван-дер-Ваальса (рассчитанные на 1 моль газа), находятся по справочным таблицам.

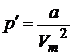– внутреннее давление, обусловленное силами взаимодействия молекул;

– "свободный" объем, доступный для движения молекул;

– "запрещенный" объем, недоступный для движения молекул,

где – объем молекулы, N_A – число Авогадро.

Уравнение Ван-дер-Ваальса

для любого числа молей

;

где – внутреннее давление;

– "свободный" объем; – "запрещенный" объем.

Постоянны Ван-дер-Ваальса связанный с критическими параметрами V_кр, р_кр, T_кр:

; ; .

VI.2 Примеры решения зада

ЗАДАЧА VI.1 Найти эффективный диаметр молекулы азота, если для азота критическая температура –147,10С; критическое давление 3,5·105Па.

Дано:t_кр= –147,1⁰С; р_кр=33,5·10⁵Па.

Найти: s - ?

Решение

Постоянная b в уравнении Ван-дер-Ваальса приближенно равна учетверенному собственному объему молекул. Поэтому для одного моля газа имеем

, (1)

где N – число Авогадро;

V₀ – объем одной молекулы, который равен ,

где s -эффективный диаметр молекулы азота.

Подставляя значения V₀ в (1), получим, что постоянная b равна .

Откуда .

Чтобы определить b, воспользуемся уравнениями, связывающими поправки Ван-дер-Ваальса с критической температурой и давлением

; .

Решая эти уравнения относительно b, получим

Подставим значение b в уравнение для эффективного диаметра молекулы, получим

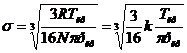, (2)

где - постоянная Больцмана.

Подставляя численные значения в (2)в системе СИ, найдем

s » 3.12·10^{-10 м.}

ЗАДАЧА VI.2.Моль кислорода расширяется адиабатически в пустоту, в результате чего объём газа увеличивается от 1 л до 10 л. Определить приращение температуры газа.

Дано: V₁ = 1 л=10^{-3 м;}V₂ = 10 л= 10 ^-2м ³; а=0,136 Па·м⁶/моль²;

Найти:

Решение

Расширяясь в пустоту, газ работы не совершает (А = 0). При адиабатическом процессе . Тогда согласно первому началу термодинамики . Внутренняя энергия моля ван-дер-ваальсовского газа с двухатомными жёсткими молекулами определяется выражением:

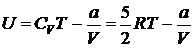Приравнивая значения этого выражения для начального и конечного состояний газа, получим, что

, откуда .

Газ охладился на 5,9 К.

VI.3. Задачи к теме «Реальные газы»

459.Вычислить критическую температуру Т_кр: 1) кислорода, 2) воды. Поправки Ван-дер-Ваальса: 1) для кислорода а = 0,136 н×м⁴/моль², в = 3,17×10^-5 м³/моль; 2) для воды: а = 0,545 н×м⁴/моль², в = 3,04×10^-5м³/моль.

460. Найти критический объем V_кр кислорода массой m=0,5 кг. Поправки Ван-дер-Ваальса: для кислорода а=0,163 н∙м⁴/моль², в=3,17∙10^-5 м³/моль.

461. В баллоне емкостью 4 л находится кислород массой m=0,15 кг при температуре 300К. Определить отношение внутреннего давления Р’ к давлению газа Р на стенки сосуда. Поправки Ван-дер-Ваальса: а=0,136 н∙м⁴/моль², в=3,04∙10^-5м³/моль.

462. В баллоне емкостью V=8 л находится кислород масссой3 кг при температуре Т=300 К. Найти, какую часть емкости занимает собственный объем молекул газа. Поправки Ван-дер-Ваальса а=0,136 н∙м⁴/моль², в=3,17∙10^-5м³/моль.

463. Вычислить критическое давление Р_кр: 1) кислорода; 2) воды. Поправки Ван-дер-Ваальса: 1) для кислорода: а=0,136н м ⁴ /моль², в=3,17 10^-5 м³/моль; 2) для воды: а=0,545н м⁴ /моль², в=3,04 10^-5 м³/моль.

464. В сосуде вместимостью V=10 л находится азот массой = 0,156 кг. Определить: 1) внутреннее давление Р^’газа; 2) собственный объем V^’молекул. Рассматривать как идеальный газ. Поправки Ван-дер-Ваальса: а=0,135 н∙м⁴/моль², в=3,86∙10^-5 м³/моль.

465. Доказать, что теплоемкость Cv газа, подчиняющего уравнению Ван-дер-Ваальса, не зависит от объема, а является функцией только температуры. Найти выражение для внутренней энергии газа Ван-дер-Ваальса, теплоемкость которого не зависит от температуры.

466. Моль азота расширяется в пустоту от начального объема 1л до конечного 10л. Найти понижение температуры Т при таком процессе, если постоянная a в уравнении Ван-дер-Ваальса для азота равна 1,35∙10⁶ атм∙см⁶ / моль².

467. Азот при критической температуре T_кр=147^°С имеет критический объем V_кр=0,12 л/моль. Считая ,что азот подчиняется уравнению Ван-дер-Ваальса, найти понижение температуры 7г азота при расширении в пустоту объема υ₁=5 л до объема υ₂=50 л.

468. Моль кислорода расширяется адиабатический в пустоту, в результате чего объём газа увеличивается от 1 л до 10 л. Определить приращение температуры газа.

469. Объем 1г азота увеличивается от 1 л до 5 л. Рассматриваем газ как реальный, найти работу внутренних сил при этом расширении.

470. В баллоне емкостью 8 л находится 0,3 кг кислорода при температуре 27˚С. Определить: какую часть объема сосуда составляет собственный объем молекул; какую часть давления газа на стенки сосуда составляет внутреннее давление, обусловленное силами притяжений молекул

471. Как изменилось бы давление газа в сосуде, если бы внезапно силы притяжения между молекулами исчезли при неизменной температуре?

472. Какое количество тепла надо подвести к одному молю газа Ван-дер-Ваальса, чтобы при расширении в пустоту от объема V₁ до объема V₂его температуре не изменилась?

473. Найти эффективный диаметр молекулы азота, если для азота критическая температура -147,1 ⁰С, критическое давления 33,5∙10⁵Па.

474. Найти постоянные уравнения Ван-дер-Ваальса для азота, если t_кразота равна -146˚С , p_кр=33 атм.

475. Найти критическую плотность воды, если критическое давление для воды P_кр=195атм, а критическая температура T_кр=374˚С, предполагая, что вода подчиняется уравнению Ван-дер-Ваальса.

476. Принимая постоянную a Ван-дер-Ваальса для воды равной 5,47∙10⁶атм∙см⁶/моль², найти внутреннее давление воды p.

477. Имеется три непрозрачных цилиндра, закрытых подвижными поршнями. Известно, что в первом цилиндре находится газ при температуре выше критической, во втором – насыщенный пар, а в третьем ненасыщенный пар. Как определить, что находится в каждом из цилиндров?

478. Моль азота охлаждается до -100 ˚С. Определить давление, оказываемое газом на стенки сосуда, если занимаемый газом объем 0,100 л.Сравнить p с p_ид,которое имел бы азот, если бы сохранил при рассматриваемых условиях свойства идеального газа.

479. Два сосуда с объемами V₁и V₂соединены трубкой с краном. В каждом из них при закрытом кране находится по одному молю одного и того же газа, подчиняющегося уравнению Ван-дер-Ваальса .До открытия крана температура газа в обоих сосудах была одинакова и равна T . Нагреется или охладится газ, если открыть кран? На сколько при этом изменится температура газа? Определить давление газа после открытия крана. Стенки сосуда и соединяющей их трубки считать адиабатическими, а теплоемкость Cv – Не зависящей от температуры.

480. Два баллона с объемами V₁₌V₂=V=1 л соединены трубкой с краном. В объеме V₁находится воздух под атмосферным давлением, а объем V₂откачен до предельного вакуума. Считая, что воздух подчиняется уравнению Ван-дер-Ваальса , а стенки баллонов и трубки адиабатические, определить, на сколько изменится температура газа после открытия крана. Начальная температура T=290 K, для воздуха a=1,39·10⁶атм·см⁶/моль².

481. Критическая температура углекислого газа СО₂ равна 31˚С, критическое давление 73 атм. Определить критический объем V_крмоля СО₂.

482. Поправки для воды в уравнении Ван-дер-Ваальса равны a=0,566 H×м⁴/моль², b=3,06×10^-5 м³/моль. Определить критический объем для 1 кг воды.

483. Найти критические параметры неона, если его постоянные в уравнении Ван-дер-Ваальса a=0,209 H×м⁴/моль², b=1,7×10^-5м³/моль.

484. Азот массой 14 кг занимает объем 0,5 м³ при температуре 0˚С. Пользуясь уравнением Ван-дер-Ваальса, найти на сколько нужно изменить температуру газа, чтобы его давление увеличилось вдвое.

485. В сосуде, объем которого 10 л, находится 360 г водяного пара при температуре 470 К. Вычислить давление пара, используя уравнение Ван-дер-Ваальса

486. Определить эффективный диаметр молекулы газа, для которого критическая температура равна 282,7 К, поправка в уравнении Ван-дер-Ваальса a=45,3×10^-2H×м⁴/моль².

487. По уравнению Ван-дер-Ваальса определить давление, под которым находится 1 моль азота в сосуде объемом 2,5 м³, если его температура 310 К.

488. Найти постоянные в уравнении Ван-дер-Ваальса для углекислого газа, если критическая температура 304 К, а критическое давление 7370 кПа.

Библиографический список

1. Савельев, И.В. Курс общей физики: в 5 кн. Кн. 1 / И.В. Савельев. – М.: Наука; Физматлит, 1989. – 350 с.

2. Трофимова, Т.И. Курс физики: Учебное пособие для инженерно-технических специальностей вузов / Т.И. Трофимова. – 9–е изд., перераб. и доп. – М,: Academia, 2004. – 558 с.

3. Трофимова, Т.И. Курс физики. / Т.И. Трофимова. – М.: Высшая школа, 2003. – 543 с.

4. Детлаф, А.А. Курс физики / А.А. Детлаф, Б.М. Яворский. – М.: Высшая школа, 2001. – 718 с.

5. Волькенштейн, В.С. Сборник задач по общему курсу физики / В.С. Волькенштейн. – М.: Наука, 1999. – 327 с.

6. Чертов, А.Г. Задачник по физике / Чертов А.Г., Воробьев А.А. – М.: Интеграл-пресс, 1997. – 544 с.

7. Трофимова, Т.И. Сборник задач по курсу физики с решениями / Т.И. Трофимова, З.Г. Павлова. – М.: Высшая школа, 2004. – 591 с.

8. Матвеев, А.Н. Молекулярная физика / А.Н. Матвеев. – М.: Высшая школа, 1987. – 360 с.

9. Грибов, Л.А. Основы физики / Грибов Л.А., Прокофьева Н.И. – М.: Гардарика, 1998. – 564 с.

10. Детлаф, А.А Справочник по физике / А.А. Детлаф, Б.М. Яворский. – М.: Наука, 1990. – 507 с.

11. Молекулярная физика и термодинамика. Учебное пособие по изучению курса для студентов инженерных специальностей всех форм обучения. / А.В. Черных. – Красноярск: СибГТУ, 2003. – 72 с.

12. Молекулярная физика и термодинамика. Черных А.В., Т.С. Розанова, И.В. Ригина. – Красноярск: СибГТУ , 2000. – 32 с.

Приложение А

(Справочное)

Таблица А.1.

Дата добавления: 2018-04-15; просмотров: 5317; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 2 3 4 5 6 7 8 91011 Следующая ⇒

Мы поможем в написании ваших работ!