III.1 Физическая кинетика. Явления переноса.
Средняя длина свободного пробега молекул газа и число столкновений в секунду
 ,
,
где  – длина свободного пробега молекул;
– длина свободного пробега молекул; 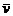 – среднеарифметическая скорость;
– среднеарифметическая скорость;  – среднее число столкновений каждой молекулы с остальными в секунду; d – эффективный диаметр молекул;
– среднее число столкновений каждой молекулы с остальными в секунду; d – эффективный диаметр молекул;  – концентрация молекул.
– концентрация молекул.
2 Явления переноса в термодинамически неравновесных системах:
Явления переноса - необратимые процессы в термодинамически неравновесных системах, в результате которых происходит пространственный перенос энергии, массы, импульса.
Диффузия.Обусловлена переносом массы. Явление диффузии для химически однородного газа подчиняется закону Фика
 ,
,
где M – масса, перенесенная за время  при диффузии;
при диффузии;  – градиент плотности в направлении, перпендикулярном к площадке
– градиент плотности в направлении, перпендикулярном к площадке  ; D – коэффициент диффузии
; D – коэффициент диффузии
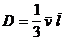 (для газа).
(для газа).
Знак минус показывает, что перенос массы происходит в направлении, противоположном вектору градиента плотности, который направлен в сторону максимального возрастания плотности.
Внутреннее трение – вязкость.Вязкость обусловлена переносом импульса. Механизм возникновения внутреннего трения между параллельными слоями газа (жидкости), движущимися с различными скоростями, заключается в том, что из-за хаотического теплового движения происходит обмен молекулами между слоями, в результате чего импульс слоя, движущегося быстрее, уменьшается, движущегося медленнее – увеличивается, что приводит к торможению слоя, движущегося быстрее, и ускорению слоя, движущемуся медленнее. Взаимодействие двух слоев согласно второму закону Ньютона можно рассматривать как процесс, при котором от одного слоя к другому в единицу времени передается импульс, по модулю равный действующей силе.
 ,
,
где F – сила внутреннего трения, действующая между слоями жидкости или газа;  – коэффициент вязкости,
– коэффициент вязкости,  (для газа);
(для газа);  – градиент скорости, направлен перпендикулярно площадке
– градиент скорости, направлен перпендикулярно площадке  .
.
Теплопроводность. Обусловлена переносом энергии. Перенос энергии в форме теплоты описывается законом Фурье
 ,
,
где Q – количество теплоты, перенесенное за время  через
через  ;
;  – коэффициент теплопроводности,
– коэффициент теплопроводности,
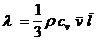 (для газа);
(для газа);
 – удельная теплоемкость при постоянном объеме;
– удельная теплоемкость при постоянном объеме;  – градиент температуры в направлении, перпендикулярном площадке
– градиент температуры в направлении, перпендикулярном площадке  .
.
Знак минус показывает, что перенос теплоты происходит в направлении, противоположном вектору градиента, который направлен в сторону максимального возрастания температуры.
Связь коэффициентов переноса 
 ,
,  .
.
III.2 Примеры решения задач
ЗАДАЧА III.1Вычислить массу и диаметр молекулы серебра, считая, что она имеет вид шарика и соприкасается с другими молекулами.
Дано:  ;
;  ;
;  =107×10-3 кг/моль;
=107×10-3 кг/моль;
 .
.
Найти: m0 - ? d - ?
Решение
Определим массу молекулы серебра  . Объем молекулы определим как объем шара
. Объем молекулы определим как объем шара  . Тогда диаметр молекулы серебра равен
. Тогда диаметр молекулы серебра равен  .
.
С другой стороны, выразим объём одной молекулы V0 через молярную массу  .
.
Подставим V0 в формулу для диаметра и получим  .
.
ЗАДАЧА III.2Рассчитать среднюю длину свободного пробега молекул азота, коэффициент диффузии и вязкость при давлении 10 5 Па и температуре 17 0С. Как изменятся найденные величины в результате двукратного увеличения объёма газа: а) при постоянном давлении; б) при постоянной температуре? Эффективный диаметр молекул азота равен 3,7·10 –8 см.
Дано: d = 3,7·10 –8 см = 3,7·10 –10 м; р = 105 Па.
Найти:  D - ?
D - ?  -?
-?
Решение
Средняя длина свободного пробега может быть рассчитана по формуле  , где
, где  . Тогда
. Тогда  . Для расчёта коэффициента диффузии по формуле
. Для расчёта коэффициента диффузии по формуле  , воспользуемся полученным результатом, определив предварительно среднюю арифметическую скорость
, воспользуемся полученным результатом, определив предварительно среднюю арифметическую скорость  . Тогда D = 1,0·10 –5 м2/с. Коэффициент вязкости рассчитаем по формуле:
. Тогда D = 1,0·10 –5 м2/с. Коэффициент вязкости рассчитаем по формуле:  .
.
Как видно из формулы, средняя длина свободного пробега зависит только от концентрации молекул. При двукратном увеличении объёма концентрация уменьшается вдвое. Следовательно, при любом процессе  . Индексы 1 и 2 соответствуют состояниям до, и после расширения газа.
. Индексы 1 и 2 соответствуют состояниям до, и после расширения газа.
В выражение коэффициента диффузии входит не только длина свободного пробега, но и средняя скорость. Следовательно, 
При постоянном давлении объём прямо пропорционален термодинамической температуре:  . Таким образом,
. Таким образом, 
 . Вязкость, зависит только от скорости молекул, следовательно, и от температуры, т.е.
. Вязкость, зависит только от скорости молекул, следовательно, и от температуры, т.е.  . Это значит, что при постоянном давлении
. Это значит, что при постоянном давлении  . При постоянной температуре коэффициент
. При постоянной температуре коэффициент  не изменяется.
не изменяется.
ЗАДАЧА III.3Вычислить коэффициенты вязкости и диффузии кислорода, находящегося при давлении 0,2 МПа и при температуре 280 К. Диаметр молекулы принять равным 0,29 нм.
Дано: р = 0,2 МПа = 2∙105Па; m= 32∙10–3 кг/моль; d = 0,29нм = 2,9∙10–10м.
Т = 280 К.
Найти:  = ?
= ? 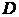 = ?
= ?
Решение.
Коэффициенты вязкости и диффузии равны соответственно
 , (1)
, (1) 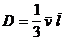 , (2)
, (2)
где  – плотность газа;
– плотность газа;
 – средняя арифметическая скорость молекул (3)
– средняя арифметическая скорость молекул (3)
 – длина свободного пробега молекул (4)
– длина свободного пробега молекул (4)
n0 – концентрация молекул.
Из соотношения р=nkT имеем  , где р – давление, k – постоянная Больцмана.
, где р – давление, k – постоянная Больцмана.
Подставляя значение  в (4), получим
в (4), получим
 .
.
Определим численное значение коэффициента диффузии, подставляя (4) и (5) в (2):

 .
.
Чтобы найти коэффициент вязкости (1), определим плотность газа  , так как
, так как  (масса 1-ой молекулы, N – число молекул);
(масса 1-ой молекулы, N – число молекул);
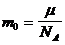 ,
,  (где
(где  ),
), 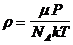 .
.
Из (1) и (2) следует, что  , то есть
, то есть

.
Дата добавления: 2018-04-15; просмотров: 360; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
