II. 1 Статистическая физика. Распределение Максвелла. Барометрическая формула.
Распределение молекул по скоростям (закон Максвелла)
Число молекул, имеющих скорости в интервале от v до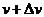 
:
,
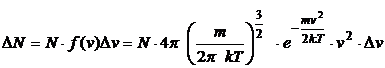где N – число всех молекул; m – масса молекулы; f(v) – функция распределения молекул по скоростям; e – основание натурального логарифма; k – постоянная Больцмана; 
– вероятность того, что 
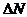число молекул будут иметь скорости в интервале от v до .
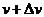Число молекул, относительные скорости которых заключены в интервале от u до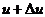 
:
,
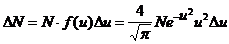где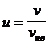 
– относительная скорость; v – скорость молекул; vнв – наиболее вероятная скорость.
Скорости молекул
Наиболее вероятная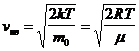 
.
Средняя арифметическая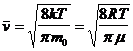 
.
Среднеквадратичная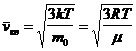 
.
Средняя кинетическая энергия молекулы
Для одноатомной молекулы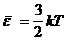 
.
Число степеней свободы молекулы
одноатомной i = 3 (3 поступат.).
двухатомной i = 5 (3 поступат. + 2 вращ.).
многоатомной i = 6 (3 поступат. + 3 вращ.).
Средняя энергия, приходящаяся на одну степень свободы
.
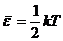Средняя энергия любой молекулы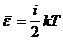 
.
Распределение молекул по энергиям
Число молекул, энергии которых заключены в интервале от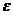 
до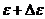 
:
,
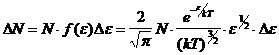где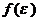 
– функция распределения молекул по энергиям.
Распределение частиц в поле силы тяжести
(Распределение Больцмана)
,
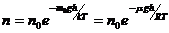где n – концентрация молекул на высоте h; n0 – концентрация молекул на высоте 0.
Распределение давления в однородном поле силы тяжести
|
|
|
(Барометрическая формула)
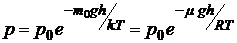
где р – давление газа на высоте h; р0 – давление газа на высоте 0.
II.2 Примеры решения задач
ЗАДАЧА II.1 Определить долю молекул водорода, модули скоростей которых при температуре 27° С лежат в интервале от 1898 м/с до 1902 м/с.
Дано: Т= 300 К ;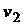 
= 1898 м/с; 
= 1902 м/с.
Найти: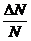 
-?
Решение
В данной задаче удобнее воспользоваться распределением молекул по относительным скоростям. Доля молекул 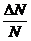, относительные скорости которых заключены в интервале от u до 
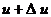, определяется формулой
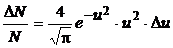, (1)
где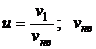 
– наиболее вероятная скорость; 
.
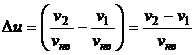С учетом этих выражений формула (1) примет вид
.
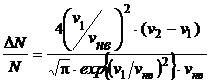Для удобства сначала вычислим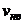 
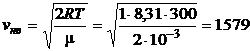(м/с)
и отношение скоростей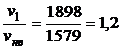 
.
Подставим численные значения в (1) и найдем долю молекул водорода, модули скоростей которых лежат в интервале от v1 до v2
.
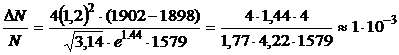ЗАДАЧА II.2 На какой высоте над уровнем моря атмосферное давление составляет 78 кПа, если температура воздуха 170С и не меняется с высотой, а давление на уровне моря нормальное? Найти число частиц в единице объема на этой высоте.
Дано: T =290 К =const ; рh = 78·103 Па; р0 = 105 Па; µ=0,029 кг/моль.
Найти: h-? n1-?
|
|
|
Решение
Температура не меняется с высотой, для нахождения давления воспользуемся барометрической формулой
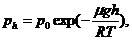
логарифмируя, получим
.
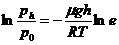Отсюда находим h
= 
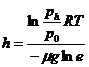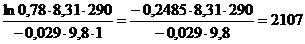м. h » 2107 м;
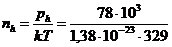=1,95·1025 м-3; nh » 1,95·1025 м-3.
ЗАДАЧА II.3 Броуновские частицы с массой 4 фг ведут себя в тепловом движении подобно гигантским молекулам, и к ним можно применить закономерности молекулярно-кинетической теории. Исходя из этого, определить, во сколько раз уменьшится концентрация броуновских частиц при увеличении высоты на 1 мм. Температуру принять равной 300 К.
Дано: m0 = 4 фг = 4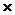 
10–15 г=4 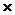10–18 кг; h = 1 мм = 10–3 м; Т = 300 К
Найти: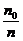 
= ?
Решение
Для броуновских частиц воспользуемся распределением молекул по высоте (распределение Больцмана)
,
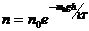где n и n0 – концентрация молекул на высоте h и на высоте h = 0, соответственно. Выразим
.
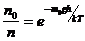Проведем вычисления, подставив численные значения,
.
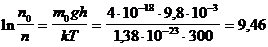е9,46=12836. Итак, 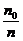= 12386, то есть концентрация частиц уменьшится в 12386 раз.
|
|
|
Дата добавления: 2018-04-15; просмотров: 647; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!