Первое начало термодинамики ( Закон сохранения и превращения энергии в термодинамике)

– интегральная форма первого начала, где 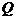 – количество теплоты, полученное системой,  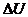– приращение внутренней энергии системы,  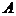– работа совершаемая системой.

 

 

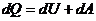
– дифференциальная форма первого начала, где dU - бесконечно малое изменение внутренней энергии системы, dA - элементарная работа, dQ - бесконечно малое количество теплоты. В этом выражении dU является полным  дифференциалом, а  dA  и  dQ таковыми не являются.

 

Общая формула для расчета количества теплоты

 

.

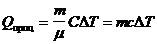Применение первого начала термодинамики к идеальным газам

 

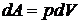 – элементарная работа.

,

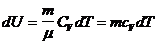где 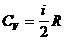 – молярная теплоемкость при постоянном объеме;

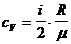 – удельная теплоемкость при постоянном объеме.

Таблица 1

Изопроцесс	1-е началотермодинамики	Теплоемкость	Количество теплоты	Совершаемая работа
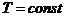(изотермич.)
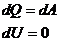
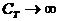
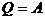
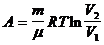
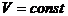(изохорич.)
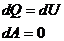
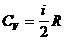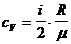
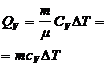
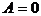
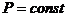(изобарич.)
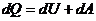
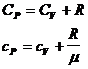
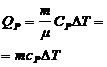
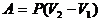
Адиабатический

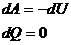
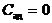
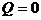
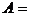
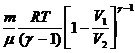
8 Адиабатический процесс.Процесс, при котором отсутствует теплообмен между системой и окружающей средой. (таблица 1) ;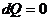

      

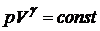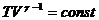1) , 2) ,  3) ;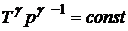

для двух состояний:

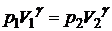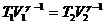  1) ,  2) , 3) ,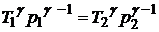

где 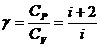 – показатель адиабаты (коэффициент Пуассона);

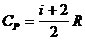 – молярная теплоемкость при постоянном давлении;

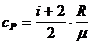     – удельная теплоемкость при постоянном давлении,

.

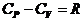IV.2 Примеры решения задач

ЗАДАЧА IV.1  Водород, масса которого 6,5 г , находящийся при температуре 27° С, расширяется вдвое при р = const за счет притока тепла извне. Найти: 1) работу расширения; 2) изменение внутренней энергии; 3) количество теплоты, сообщенное газу.

Дано: 6,5 г=6,5∙10^{-3 кг; р =} const;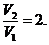

Найти: А-? DU-? Q-?

 

Решение

Приступая к решению задачи, прежде всего надо выявить характер процесса, протекающего в газе, и использовать соответствующие формулы табл.1.

1. Вычислим значения молярных теплоемкостей водорода, учитывая, что молекулы водорода двухатомные и число степеней свободы i = 5:

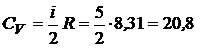Дж/(моль К),

.

 

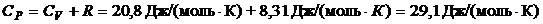2. Используя условие задачи и уравнение для изобарического процесса 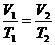, найдем температуру газа после расширения:

.

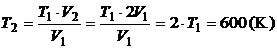3. Вычислим изменение внутренней энергии и количество теплоты:

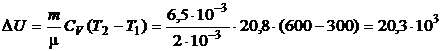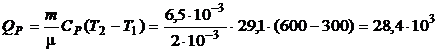(Дж),

(Дж).

4. На основании первого начала термодинамики найдем работу расширения газа

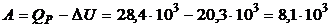(Дж).

 

ЗАДАЧА IV.2  Двухатомный идеальный газ, занимающий при давлении

р₁ = 3×10⁵ Па объем V₁= 4 л, расширяется до объема V₂= 6 л, при этом давление падает до значения р₂ = 10⁵ Па. Процесс происходит сначала по адиабате, затем по изохоре (рисунок 12). Определить работу сил давления газа, изменение его внутренней энергии и количество поглощенной теплоты при этом переходе.

Дано: р₁ = 3×10⁵ Па ;  р₂ = 10⁵ Па; V₁= 4 л = 4 ×10 м^-3; V₂= 6 л=6 ×10 м^-3 .

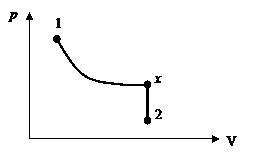Найти: А-? DU-? Q-?

 

Решение

1. Газ участвует в двух процессах: а) адиабатное расширение из состояния 1 в некоторое состояние x, в котором объем

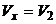                                          (1)

 

       Рисунок 12

давление р_x не известно; б) изохорный процесс из состояния x в состояние 2. Найдем р_x из уравнения адиабаты для двух состояний

Рис.1

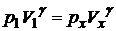.                                   (2)

Для двухатомного газа i = 5, следовательно

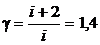.                                            (3)

Значение р_х получим на основании (1), (2) и (3), а именно

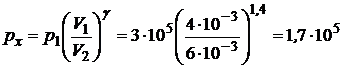(Па).

Откуда видим, что 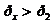, и процесс 1-2 можно представить графически (рис.1).

Учтем, что 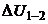 не зависит от вида процесса, а зависит только от начального и конечного состояний. Следовательно,

.

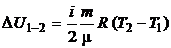Из уравнения Клапейрона - Менделеева для состояний 1 и 2 имеем

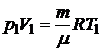            и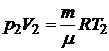 

откуда получим

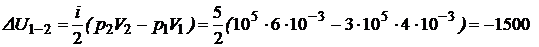(Дж)

а это значит, что газ охлаждается.

2. Работу А_1-2найдем как сумму работ: 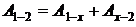, где для изохоры х–2 А_х–2 = 0, для адиабаты 1–х:

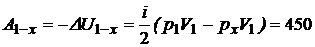 (Дж),

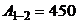т.е. (Дж).

3. Количество теплоты Q_1-2 складывается также как сумма теплот: 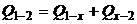, где (табл.1) для адиабаты Q _1–x = 0, для изохоры х–2:

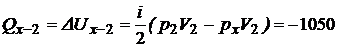(Дж),

т.е. 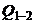 = – 1050 Дж, а это значит, что газ отдает тепло.

 

ЗАДАЧА IV.3При изобарическом расширении некоторой массы двухатомного газа, находящегося под давлением 10⁵Па, его внутренняя энергия изменилась на 490 Дж. Найти приращение объема газа.

Дано:    р=10⁵ Па; DU=490 Дж; g = 1,4.

Найти: DV - ?

Решение

Чтобы определить приращение объема DV при изобарическом расширении, нужно знать работу, произведенную газом при этом процессе: .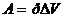

Работу можно вычислить и на основании первого начала термодинамики: 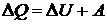   , откуда следует, что .

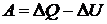Количество тепла DQ, сообщенное при изобарическом расширении произвольной массе газа, равно:   .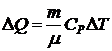

Изменение внутренней энергии DU, которое произойдет при этом .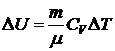

Разделив 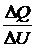, получим:          , .

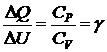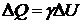Подставим это значение в уравнение для работы:

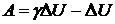, или .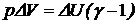

Отсюда найдем, что 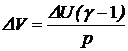.         DV = 1,96·10^{-3 м3}.

 

---

Дата добавления: 2018-04-15; просмотров: 313; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!