Основные термодинамические параметры
Состояние некоторой массы газа m определяется тремя
термодинамическими параметрами: р, V, T. Здесь р - давление, V – объем, Т – температура.
Температура – физическая величина, характеризующая состояние термодинамического равновесия макроскопической системы и определяющая направление теплообмена между телами. Температура – одно из основных понятий, играющих важную роль не только в термодинамике, но и в физике в целом.
Закон, выражающий зависимость между этими параметрами, называется уравнением состояния
f (р, V, T) = 0.
Дополнительные термодинамические параметры
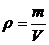– плотность вещества.
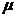– молярная масса (масса одного моля).
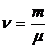– число молей.
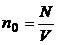– концентрация молекул , где N число всех молекул в объеме V.
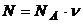, где 
– число Авогадро (число молекул в 1 моле,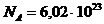 
моль-1).
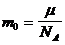– масса одной молекулы любого вещества.
3 Идеальный газ.
Модель, согласно которой:
а) собственный объем молекул газа пренебрежимо мал по сравнению с объемом сосуда;
б) между молекулами газа отсутствуют силы взаимодействия;
в) столкновения молекул газа между собой и со стенками сосуда абсолютно упругие.
Термодинамические процессы
Термодинамический процесс- любое изменение в термодинамической системе, связанное с изменением хотя бы одного из ее термодинамических параметров.
|
|
|
Изотермический(закон Бойля-Мариотта)
При T = const; m = const; рV = const.
Для 2-х состояний
р1V1 = р2V2.
Изобарический(закон Гей-Люссака)
При р = const; m = const; V = V0( 1 +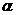 
t );
Для 2-х состояний 
.
Изохорический (закон Шарля)
При V = const; m = const; р = р0( 1 + 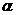t );
Для 2-х состояний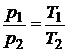 
.
Уравнение состояния идеального газа
Для данной массы газа (закон. Клапейрона):
.
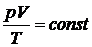Для 2-х состояний
.
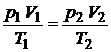Для любой массы газа (уравнение Клапейрона-Менделеева):
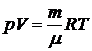или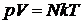 
,
где N – число молекул; R = 8,31 Дж/(моль∙К) универсальная газовая постоянная; k = 1,38×10–23 Дж/К – постоянная Больцмана; R =kNаоткуда следует
,
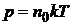где n0 – концентрация молекул.
Закон Авогадро
Моли любых газов при одинаковой температуре и давлении занимают одинаковые объемы.
Нормальные условия
(р0 = 1,01×105 Па, T = 273,15 К); 
= 22,41∙10–3 м3/моль.
Давление смеси газов (закон Дальтона)
,
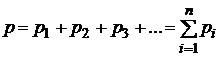где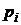 
– парциальное давление i-го газа,
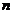– число газов в смеси.
Парциальное давление-давление, которое оказывали бы газы смеси, если бы они занимали объем, равный объему смеси при той же температуре.
Масса 1 моля смеси газов
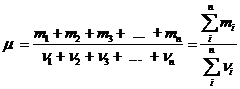
где mi – масса i-го газа, входящего в смесь;
|
|
|
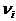– число молей i-го газа, находящегося в смеси.
Основное уравнение кинетической теории газов
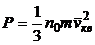или 
,
где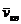 
– среднеквадратичная скорость молекул; 
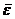– средняя кинетическая энергия поступательного движения одной молекулы.
I. 2 Примеры решения задач
ЗАДАЧА I.1 Найти молярную массу воздуха, считая, что он состоит по массе из одной части кислорода и трех частей азота.
Дано:mв = m1 +3m1 .
Найти: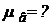
Решение
Воздух, являясь смесью идеальных газов, тоже представляет идеальный газ, и к нему можно применить уравнение Клапейрона -Менделеева
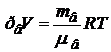. (1)
Для каждой компоненты смеси кислорода и азота запишем соответствующее уравнение:
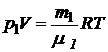, (2)
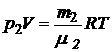, (3)
где р1 и р2 – парциальные давления кислорода и азота.
По закону Дальтона pв = p1+ p2. Складываем (2) и (3), получим
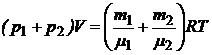(4)
или на основании закона Дальтона
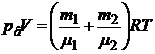. (5)
Сравнивая, (1) и (5) и учитывая, что mв = m1 + m2 , имеем
,
откуда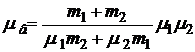 
(6)
Подставляя в (6) m2= 3m1(по условию), найдем молярную массу воздуха
|
|
|
,
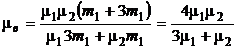где m1 = 32×10-3 кг/моль, m2 = 28×10-3 кг/моль. Подставляя значения, получим
m = 29×10-3 кг/моль.
ЗАДАЧА I. 2В баллоне находится идеальный газ. Когда часть газа выпустили, температура газа в баллоне уменьшилась в 3 раза, а давление – в 4 раза. Какую часть газа выпустили?
Дано: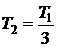 
; 
.
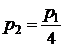Найти: 
Решение
Для двух состояний уравнениеКлапейрона -Менделеева имеют вид:
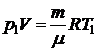и 
, где m – начальная масса газа,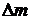 
- выпущенная из баллона масса газа. Объём баллона V не изменялся. Решая эти их уравнения совместно, находим 
.
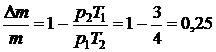ЗАДАЧА I. 3 В сосуде емкостью 3,5 л находится смесь газов, в которую входит 2·1015 молекул кислорода, 5·1015 молекул азота и 6,6·10-7г аргона. Какова температура смеси, если давление в сосуде 1,74·10-4 мм.рт.ст.?
Дано: V = 3,5 л =3,5·10 –3 м3 ; n1 = 2·1015 ; n2= 5·1015; m3= 6,6·10-10 кг ;
р= 1,74·10-4 мм.рт.ст.=2,31·10-2Па ; µ = 0,040 кг/моль.
Найти: Т-?
Решение
На основании закона Дальтона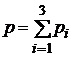 
, где парциальное давление равно 
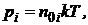а число молекул можно определить как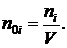 
Для аргона число молекул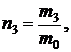 
где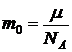 
- масса одной молекулы аргона.
Тогда давление смеси газов будет равно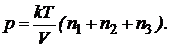 
Отсюда искомая температура смеси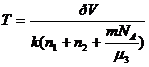 
. Подставляя численные значения, получим Т = 346 К.
|
|
|
Дата добавления: 2018-04-15; просмотров: 453; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!