Линейные неоднородные дифференциальные уравнения n-го порядка с постоянными коэффициентами. Метод подбора.

Рассмотрим линейное неоднородное дифференциальное уравнение

y⁽ⁿ⁾ + a_n-1y^{(n - 1)} + ... + a₁y' + a₀y = f(x).

Коэффициенты a_n-1, ... , a₁, a₀ — постоянные действительные числа, f(x) — непрерывная на [a, b] правая часть.

Общее решение этого уравнения имеет вид y(x) = C₁y₁(x) + C₂y₂(x) + ... + C_ny_n(x) + y*(x),

где С₁, С₂, ..., С_n — произвольные постоянные, y₁(x), y₂(x), ..., y_n(x) — фундаментальная система решений однородного уравнения, y*(x) — частное решение неоднородного уравнения. Частное решение y*(x) можно найти методом подбора, если правая часть уравнения — квазимногочлен — функция вида : f(x) = exp(αx)(M_m(x)cos(βx) + N_n(x)sin(βx)).

Здесь M_m(x) — многочлен степени m, N_n(x) — многочлен степени n, α и β — действительные числа.

Метод подбора вычисления частного решения линейного неоднородного уравнения с квазимногочленом в правой части состоит в том, что частное решение уравнения

отыскивают в виде : y*(x) = exp(αx)(P_k(x)cos(βx) + Q_k(x)sin(βx))x^r, где P_k(x) и Q_k(x) — многочлены степени k = max(n, m) с неизвестными коэффициентами,

P_k(x) = p_kx^k + p_k-1x^k-1 + ... + p₁x + p₀, Q_k(x) = q_kx^k + q_k-1x^k-1 + ... + q₁x + q₀.

Для того чтобы найти неизвестные коэффициенты многочленов P_k(x) и Q_k(x) , подставляем y*(x) = exp(αx)(P_k(x)cos(βx) + Q_k(x)sin(βx)) в уравнение и приравниваем в правой и левой части полученного равенства коэффициенты при

exp(αx)cos(βx), exp(αx)sin(βx), xexp(αx)cos(βx), xexp(αx)sin(βx), x²exp(αx)cos(βx), x²exp(αx)sin(βx), ..., x^kexp(αx)cos(βx), x^kexp(αx)sin(βx).

Полученная таким образом система 2k + 2 уравнений относительно 2k + 2 неизвестных имеет единственное решение.

Метод подбора применяется к ограниченному, но достаточно широкому классу правых частей, поскольку квазимногочленами являются функции вида:

M_k(x), M_k(x)exp(αx), M_k(x)cos(βx), M_k(x)sin(βx), exp(αx)(M_m(x)cos(βx) + N_n(x)sin(βx)).

 

 

Системы дифференциальных уравнений. Основные понятия. Задача Коши и теорема существования и единственности задачи Коши для нормальных систем. Линейные системы дифференциальных уравнений. Фундаментальная матрица однородной системы. Структура общего решения.

Определение: совокупность двух или более дифференциальных уравнений называется системой дифференциальных уравнений. Данная совокупность может быть представлена в виде: .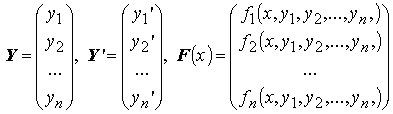

Задача Коши: найти такое решение Y = Y(x) системы Y' = F(x,Y), что Y(x₀)=Y₀, где Y₀ — некоторый постоянный вектор.

Теорема Коши. Пусть в области D из Rⁿ⁺¹ непрерывны все компоненты вектора правой части F(x,Y) и их частные производные по Y: 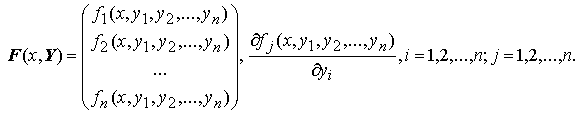Тогда, какова бы ни была начальная точка (x₀,Y₀) ≡ (x₀,y_{1, 0} ,y_{2, 0}, … ,y_{n, 0} ) ∈ D , существует такой отрезок [x₀ − h; x₀ + h] , что задача Коши Y' = F(x,Y), что Y(x₀)=Y₀ имеет единственное решение.

 Система линейных дифференциальных уравнений имеет вид : 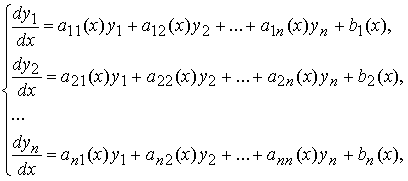где a_ij(x) и b_i (x) — известные, а y_j (x) — неизвестные функции, (i = 1,2, … ,n, j = 1,2, … , n).

Фундаментальная матрица системы: Матрица Φ, столбцами которой являются n линейно независимых на [a, b] решений Y₁(x), Y₂(x), ..., Y_n(x) однородной линейной системы Y' = A(x)Y называется фундаментальной матрицей решений системы: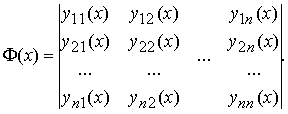

 

Теорема о структуре общего решения системы.

Если матрица A(x) неперерывна на [a, b], то общее решение системы Y' = A(x)Y имеет вид

Y(x) = Φ(x)·C ≡ C₁·Y₁(x) + C₂·Y₂(x) + ... + C_n· Y_n(x),

где Φ(x) — фундаментальная матрица решений однородной линейной системы, Y₁(x), Y₂(x), ..., Y_n(x) — столбцы этой фундаментальной матрицы решений, C— произвольный постоянный вектор-столбец.

 

---

Дата добавления: 2018-04-15; просмотров: 620; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!