Линейные дифференциальные уравнения высших порядков. Задача Коши. Теорема существования и единственности задачи Коши.(ВОПРОС 16)

Линейные дифференциальные уравнения высших порядков – уравнения, имеющие вид  и  , где функции f_n…f₀ называются коэффициентами уравнения, а правая часть f(x) – неоднородностью этого уравнения (если неоднородность в уравнении отсутствует f(x)= 0, то уравнение является однородным)

Задача Коши: в случае уравнения первого порядка задавалось всего одно начальное условие. Для дифференциальных уравнений n-го порядка таких условий должно быть n.Именно: пусть (x_0, y_0,y₁⁰….,y⁰_(n-1)) - фиксированная точка области D (область определения уравнения).Задача отыскания решения y=y(x) уравнения, удовлетворяющего начальным условиям y(x₀)=y_0,y’(x₀)=y₁⁰,….y^(n-1)(x₀)=y_n-1⁰ называется начальной задачей или задачей Коши.

Теорема Коши: пусть функция f(x,y,y_1….y_n-1)  и ее частные производные непрерывны на области D.Тогда какова бы ни была начальная точка (x_0, y_0,y₁⁰….,y⁰_(n-1)), лежащая внутри данной области, существует такое число h>0, такое что задача Коши имеет решение на отрезке [x₀-h;x₀+h] и это решение единственно на данном отрезке.

Линейная зависимость и линейная независимость системы функций. Линейные однородные дифференциальные уравнения n-го порядка. Фундаментальная система решений. Структура общего решения.(ВОПРОС17)

Функции y₁(x)….y_n(x) называются линейно независимыми на промежутке [a,b], если существует только тривиальное решение уравнения λ₁y₁ + λ₂y₂ + λ₃y₂+…. λ_ny_n = 0 относительно коэффициентов λ. В противном случае функции называют линейно зависимыми. Другими словами, функции линейно зависимы, если хотя бы одна из них может быть представлена в виде линейной комбинации остальных.

Теорема: Функции y₁(x), y₂(x), ..., y_n(x) линейно зависимы на отрезке [a;b] тогда и только тогда, когда хотя бы одна из них является на этом отрезке линейной комбинацией других .

Очевидны следующие утверждения.

• Если среди функций y₁(x), y₂(x), ..., y_n(x) есть нулевая функция, то функции линейно зависимы.

• Если функции y₁(x), y₂(x), ..., y_k(x) линейно зависимы, то при любых y_{k + 1}(x), y_{k + 2}(x), ..., y_n (x) функции y₁(x), y₂(x), ..., y_k(x), y_{k + 1}(x), ...,y_n(x) также линейно зависимы.

• Если функции y₁(x), y₂(x), ..., y_n(x) линейно зависимы на отрезке [a;b] , то они линейно зависимы и на любом отрезке, лежащем внутри[a;b] .

• Если функции y₁(x), y₂(x), ..., y_n(x) линейно независимы на [a;b] , то они линейно независимы и на любом отрезке, содержащем отрезок[а;b] (если, они определены на этом отрезке).

Вектор–функции Y₁(x), Y₂(x), ..., Y_n(x),

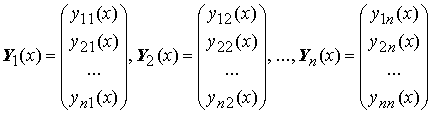
называются линейно зависимыми на отрезке [a;b] , если существуют постоянные α₁, α₂, ..., α_n , не равные нулю одновременно и такие, что

α₁ Y₁(x) + α₂ Y₂(x) + ... + α_n Y_n(x) =0

для всех x из отрезка [a;b].

В противном случае функции Y₁(x), Y₂(x), ..., Y_n(x) называются линейно независимыми.

Линейным однородным дифференциальным уравнением (ЛОДУ) n – го порядка называется уравнение вида:

Теорема о необходимых и достаточных условиях линейной независимости системы функций:

Для того, чтобы система функций y₁(x)….y_n(x) была линейно независимой для всех х из промежутка [a, b] (∀x ∈[a, b]), необходимо и достаточно, чтобы определитель Вронского (вронскиан) detW, составленный из этих функций, был отличен от нуля (det W ≠ 0):

 

Рассмотрим линейное однородное дифференциальное уравнение y⁽ⁿ⁾ + a_n-1(x)y^{(n - 1)} + ... + a₁(x)y' + a₀(x)y = 0. Фундаментальной системой решений однородного линейного дифференциального уравнения называется упорядоченный набор из n линейно независимых решений уравнения. Иными словами любые n линейно независимых решений y₁(x), y₂(x),..., y_n(x) уравнения y⁽ⁿ⁾ + a_n-1(x)y^{(n - 1)} + ... + a₁(x)y' + a₀(x)y = 0 образуют фундаментальную систему решений.

Рассмотрим на [a; b] линейное однородное дифференциальное уравнение y⁽ⁿ⁾ + a_n-1(x)y^{(n - 1)} + ... + a₁(x)y' + a₀(x)y = 0. Общим решением этого уравнения на отрезке [a;b] называется функция y = Φ(x, C₁,..., C_n ), зависящая от n произвольных постоянныхC₁,..., C_n и удовлетворяющая следующим условиям :

− при любых допустимых значениях постоянных C₁,..., C_n функция y = Φ(x, C₁,..., C_n ) является решением уравнения на [a; b] ;

− какова бы ни была начальная точка (x₀, y₀, y_1,0 ,..., y_{n − 1,0} ) , x₀∈ [a;b] , существуют такие значения C₁ =C₁₀ , ..., C_n = C_n0 , что функцияy = Φ(x, C₁₀ , ..., C_n0) удовлетворяет начальным условиям y(x₀) = y₀, y '(x₀) = y_1,0 ,..., y^{(n − 1)} (x₀) = y_{n− 1,0} .

Справедливо следующее утверждение ( теорема о структуре общего решения линейного однородного уравнения).

Если все коэффициенты уравнения линейного однородного дифференциального уравнения непрерывны на отрезке [a;b] , а функции y₁(x), y₂(x),..., y_n(x) образуют фундаментальную систему решений этого уравнения, то общее решение уравнения имеет вид y(x,C₁,..., C_n) = C₁ y₁(x) + C₂ y₂(x) + ... + C_n y_n(x), где C₁,...,C_n — произвольные постоянные.

 

---

Дата добавления: 2018-04-15; просмотров: 360; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!