Линейные дифференциальные уравнения первого порядка. Методы Лагранжа и Бернулли.(ВОПРОС14)
Дифференциальное уравнение называется линейным, если в нём функция и все её производные содержатся только в первой степени, отсутствуют и их произведения. Общий вид линейного дифференциального уравнения первого порядка таков:  , где
, где 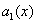 и
и  - непрерывные функции от x.
- непрерывные функции от x.
Методы решения линейных дифференциальных уравнений:
1.Метод Лагранжа.
Рассмотрим линейное неоднородное дифференциальное уравнение y(n) + an-1(x)y(n- 1) + ... + a1(x)y' + a0(x)y = f(x).
с нерерывными на [a; b] коэффициентами и непрерывной правой частью.
Предположим, что известна фундаментальная система y1(x), y2(x),..., yn(x) решений соответствующего однородного уравнения y(n) + an-1(x)y(n- 1) + ... + a1(x)y' + a0(x)y = 0.
Будем искать частное решение неоднородного уравнения в виде
y*(x) = C1(x) y1(x) + C2(x) y2(x) + ... + Cn(x) yn(x) ,
где C1(x), C2(x) , ... , Cn(x) — неизвестные, n раз дифференцируемые на [a; b] функции. Их называют варьируемые постоянные общего решения однородного уравнения.
Справедливо следующее утверждение.
Пусть y1(x), y2(x),..., yn(x) — фундаментальная система решений однородного уравнения y(n) + an-1(x)y(n- 1) + ... + a1(x)y' + a0(x)y = 0 с непрерывными на отрезке [a; b] коэффициентами. Если правая часть f(x) неоднородного уравнения y(n) + an-1(x)y(n- 1) + ... + a1(x)y' + a0(x)y = f(x) непрерывна на [a; b], то его частное решение можно искать в виде
y*(x) = y(x,C1,..., Cn) = C1(x) y1(x) + C2(x) y2(x) + ... + Cn(x) yn(x) .
Неизвестные функции C1(x), C2(x) , ... , Cn(x) находятся из системы

2. Метод Бернулли.
Решение линейного дифференциального уравнения необходимо представить в виде произведения двух неизвестных функций y=u*v от аргумента u=u(x), v=v(x). Одну из этих функций можно выбрать произвольно, а вторая определяется из дифференциального уравнения.
|
|
|
2. По правилу производная произведения равна y=u*v, то y'=u'v+uv'.
3. Подставим запись функции y=u*v и производной y'=u'v+uv' в уравнение y'+p(x)*y=g(x) и получим u'v+uv'+p(x)*u*v= g(x). Сгруппируем второй и третий слагаемые, вынеся общий множитель (u) за скобки и придем к диф. уравнению u'v+u(v'+p(x)*v)=g(x).
4. Сперва определяем частное решение v=v(x), для этого решаем диф. уравнения v'+p(x)*v=0 и за произвольную постоянную интегрирования берем ноль (С=0). Данное уравнение является дифференциальным уравнением с разделяющимися переменными.
5. Далее подставим найденную функцию v=v(x) в исходное диф. уравнение u'v+uv'+p(x)*u*v= g(x), которое при этом упростится до вида u'v+u*0=g(x), то есть к дифференциальному уравнению с разделяющимися переменными u'v(х)=g(x) относительно u(x). Из этого уравнения находим u=u(x)+С.
6. Имея u=u(x) и v=v(x) находим общее решение ДУ через произведение y=u*v=( u(x)+С)* v(x).
7. Если задана задача Коши то с дополнительной условия на решение y(x0)=y0 определяем старую С.
Дифференциальные уравнения высших порядков. Задача Коши. Теорема существования и единственности задачи Коши. Общее решение. Дифференциальные уравнения, допускающие понижение порядка.
|
|
|
Определение: если дифференциальное уравнение F(x,y,y’,….y(n))=0 содержит производную неизвестной функции y=y(x) порядка выше первого (n>1), то его называют уравнением высшего порядка.
Задача Коши: в случае уравнения первого порядка задавалось всего одно начальное условие. Для дифференциальных уравнений n-го порядка таких условий должно быть n.Именно: пусть (x0, y0,y10….,y0(n-1)) - фиксированная точка области D (область определения уравнения).Задача отыскания решения y=y(x) уравнения, удовлетворяющего начальным условиям y(x0)=y0,y’(x0)=y10,….y(n-1)(x0)=yn-10 называется начальной задачей или задачей Коши.
Теорема Коши: пусть функция f(x,y,y1….yn-1) и ее частные производные непрерывны на области D.Тогда какова бы ни была начальная точка (x0, y0,y10….,y0(n-1)), лежащая внутри данной области, существует такое число h>0, такое что задача Коши имеет решение на отрезке [x0-h;x0+h] и это решение единственно на данном отрезке.
Общее решение в области Q ⸦ D называется функция y= Ф(х, С1,…Сn), зависящая от n произвольных постоянных С1,…Сn, удовлетворяющая следующим требованиям:
1. при любом допустимом значении постоянных С1,…Сn функция y= Ф(х, С1,…Сn) является решением дифференциального уравнения на некотором отрезке [a,b] .
|
|
|
2. какова бы ни была начальная точка (x0, y0,y10….,y0(n-1))) ϵ Q существуют постоянные С1=С10,… Сn=Cn0 такие, что функция y=Ф(х, С1,…Сn),является решением именно этой задачи Коши.
Дифференциальные уравнения, допускающие понижение порядка:
1. Уравнение не содержит и
и
Это дифференциальное уравнение вида  . Произведём замену переменной: введём новую функцию
. Произведём замену переменной: введём новую функцию  и тогда
и тогда  . Следовательно,
. Следовательно,  и исходное уравнение превращается в уравнение первого порядка
и исходное уравнение превращается в уравнение первого порядка  с искомой функцией
с искомой функцией  .Решая его, находим
.Решая его, находим 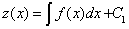 . Так как
. Так как  , то
, то  .Отсюда, интегрируя ещё раз, получаем решение исходного уравнения:
.Отсюда, интегрируя ещё раз, получаем решение исходного уравнения:  ,где
,где  и
и  - произвольные константы интегрирования.
- произвольные константы интегрирования.
2.Уравнение не содержит
Это дифференциальное уравнение вида  . Произведём замену переменной как в предыдущем случае: введём
. Произведём замену переменной как в предыдущем случае: введём  , тогда
, тогда  , и уравнение преобразуется в уравнение первого порядка
, и уравнение преобразуется в уравнение первого порядка  . Решая его, найдём
. Решая его, найдём  . Так как
. Так как  , то
, то  .Отсюда, интегрируя ещё раз, получаем решение исходного уравнения:
.Отсюда, интегрируя ещё раз, получаем решение исходного уравнения:  ,где
,где  и
и  - произвольные константы интегрирования.
- произвольные константы интегрирования.
3.Уравнение не содержит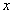
Это уравнение вида  . Вводим новую функцию
. Вводим новую функцию  , полагая
, полагая  . Тогда
. Тогда
 .
.
Подставляя в уравнение выражения для  и
и  , получаем уравнение первого порядка относительно z как функции от y:
, получаем уравнение первого порядка относительно z как функции от y:  .Решая его, найдём
.Решая его, найдём  . Так как
. Так как  , то
, то 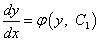 . Получено дифференциальное уравнение с разделяющимися переменными, из которого находим общее решение исходного уравнения:
. Получено дифференциальное уравнение с разделяющимися переменными, из которого находим общее решение исходного уравнения:  ,где
,где  и
и  - произвольные константы интегрирования.
- произвольные константы интегрирования.
|
|
|
Дата добавления: 2018-04-15; просмотров: 1364; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
