Двойной интеграл в полярных координатах.

Двойные интегралы: определение, условия существования, основные свойства, сведение к повторным интегралам.(ВОПРОС 1)

Определение: Двойным интегралом от функции f (x,y) по области D называется конечный предел двумерной интегральной суммы, вычисленный при стремлении к нулю ранга разбиения, порождающего эту сумму.

Достаточное условие существования двойного интеграла:

Если функция z = f(x, y) непрерывна в замкнутой области D, то двойной интеграл от функции f (x, y) по области D существует.

Основные свойства: 1°. Аддитивность. Если функция f(x, y) интегрируема в области D и если область D при помощи кривой Г площади нуль разбивается на две связные и не имеющие общих внутренних точек области D1 и D2, то функция f(x, y) интегрируема в каждой из областей D1 и D2, причем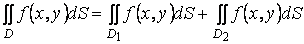

2°. Линейное свойство. Если функции f(x, y) и g(x, y) интегрируемы в области D, а α и β - любые вещественные числа, то функция [α · f(x, y) + β · g(x, y)] также интегрируема в области D, причем

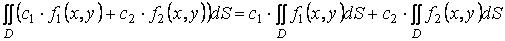,где С₁ и С₂-константы.

3°. Если функции f(x, y) и g(x, y) интегрируемы в области D, то и произведение этих функций интегрируемо в D.

4°. Если функции f(x, y) и g(x, y) обе интегрируемы в области D и всюду в этой области f(x, y) ≤ g(x, y), то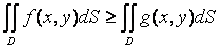

5°. Оценка двойного интеграла снизу и сверху: если 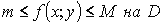,то S-площадь области D.

6°. Теорема о среднем значении. Если функция f (x,y) непрерывна в области D, то существует хотя бы одна точка P₀(x₀,y₀)ϵD, такая что 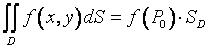.Число 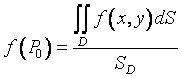называется средним значением функции f (x,y) в области D.

Доказательство: Если f(x; y) непрерывна на D, то существуют наименьшее m и наибольшее М значения функции f(x; y),т.е 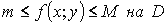по свойству 5 имеем 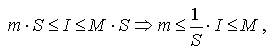то есть число I/S находится между m и М.

Но непрерывная функция f (x; y) принимает все промежуточные от m до М значения 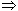существует точка M_* D: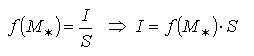

Сведение к повторным интегралам:

Теорема 1(Фубини).Если 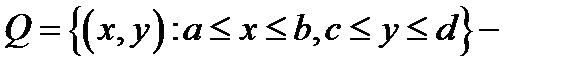прямоугольник и если функция 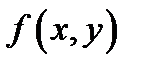кусочно непрерывна в 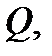то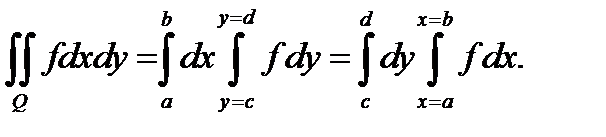

Теорема 2 (вычисление двойного интеграла в криволинейной области). Если 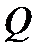имеет вид 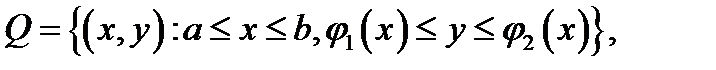где функции 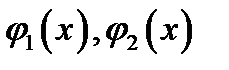непрерывны на отрезке 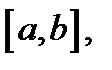и если функция 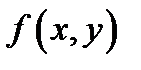непрерывна в 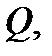то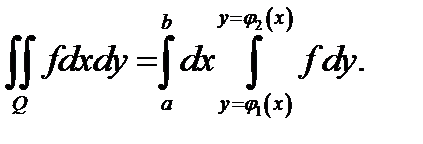

Доказательство: Обозначим 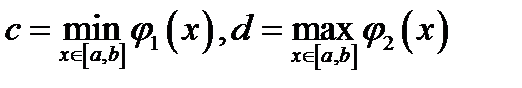, 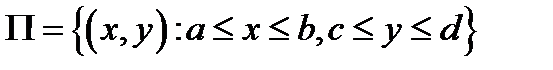и рассмотрим функцию

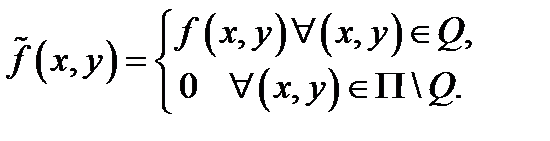
Эта функция кусочно непрерывна в 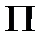, поэтому применима теорема Фубини:

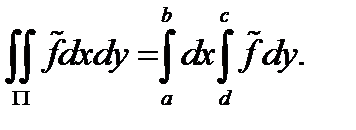
Так как

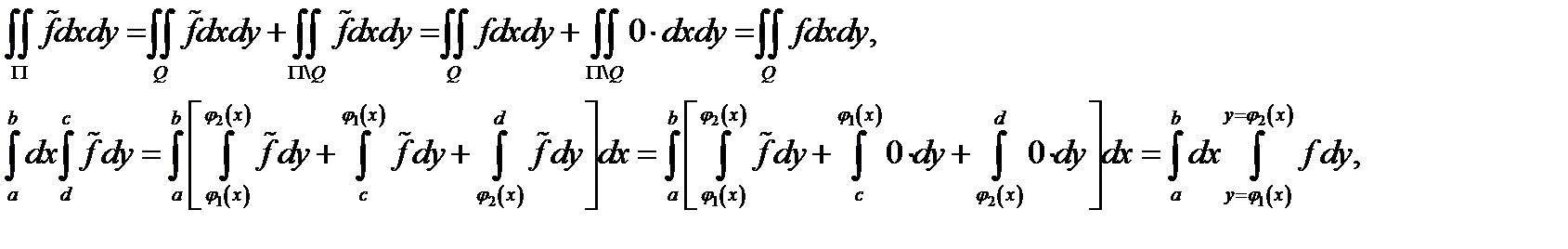
то 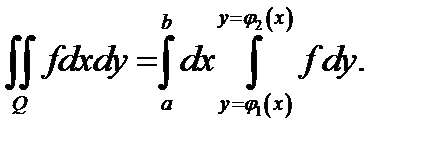Теорема доказана.

2. Замена переменных в двойном интеграле. Якобиан и его геометрический смысл. Переход к полярным координатам.(ВОПРОС 2)

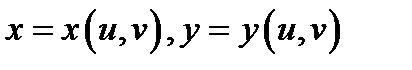
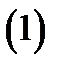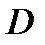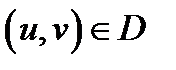Определение 1.Говорят, что функции задают взаимно однозначное соответствие области на область если каждой точке соответствует единственная точка 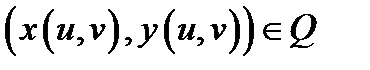и двум различным точкам из области 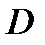соответствуют две различные точки из области 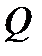по закону (1).

Определение 2.Пара 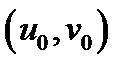только что описанных чисел называется криволинейными координатами точки 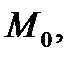а кривые

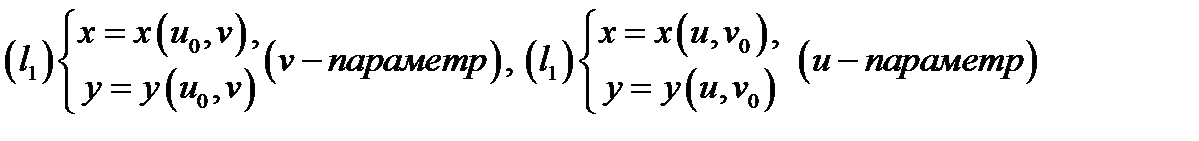
называются координатными линиями точки 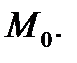Таким образом, в области 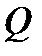можно задать две системы координат: 1) декартову прямоугольную систему координат, определяемую сеткой взаимно ортогональных прямых 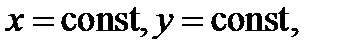и криволинейную систему координат, определяемую сеткой координатных линий и

Определение 3.Определитель 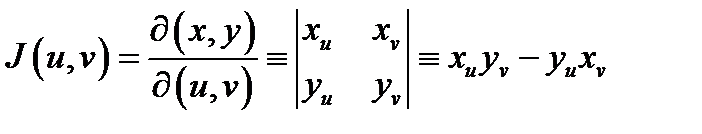называется якобианом отображения (1) или якобианом перехода от декартовых координат к криволинейным.Можно показать, что 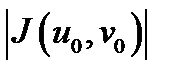равен коэффициенту искажения площадей (геометрический смысл якобиана), т.е. если 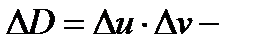площадь малого прямоугольника с одной из вершин 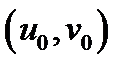и ребрами 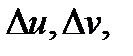а площадь криволинейного четырёхугольника, являющегося образом указанного прямоугольника при отображении (1), то 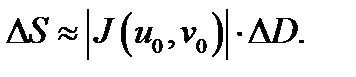Используя этот факт, можно доказать следующее утверждение.

Теорема 1. Имеет место равенство 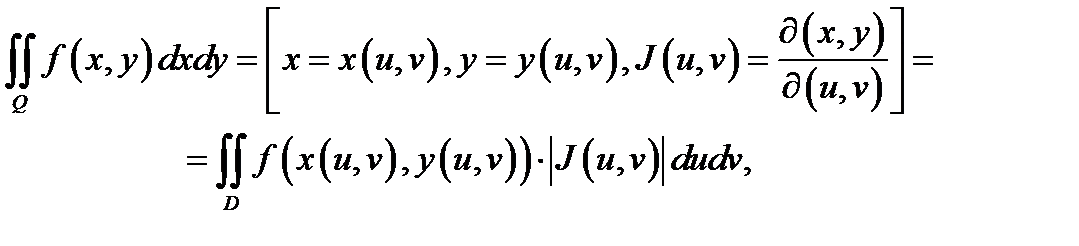если выполнены следующие условия:

1) функция 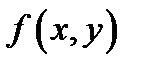непрерывна в замкнутой ограниченной области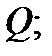

2) функции 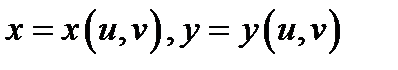непрерывно дифференцируемы в области 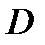и взаимно однозначно отображают область 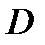на область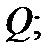

3) якобиан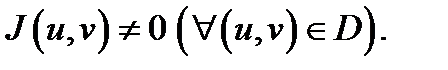

Двойной интеграл в полярных координатах.

Рассмотрим функции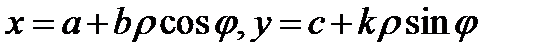

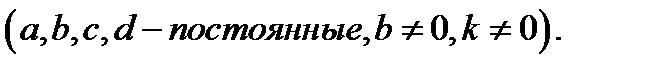
Эти функции будут взаимно однозначно отображать плоскость переменных 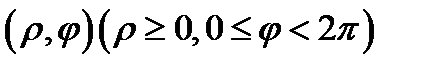на плоскость переменных 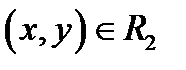, если условиться, что точка 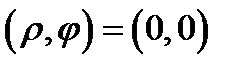переходит только в точку 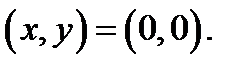Криволинейные координаты 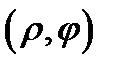называют в этом случае обобщенными полярными координатами, а в случае 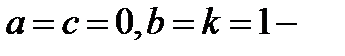просто полярными координатами в плоскости 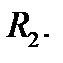Вычислим якобиан перехода для таких координат. Имеем

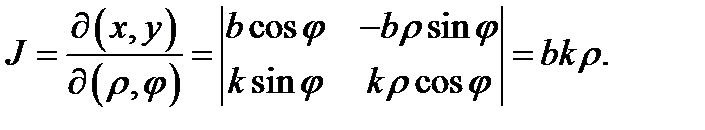
Из теоремы 1 вытекает, что двойной интеграл в обобщенных полярных координатах будет таким:

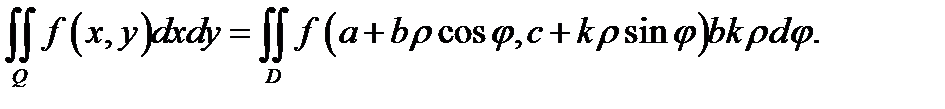
При 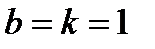получаем формулу

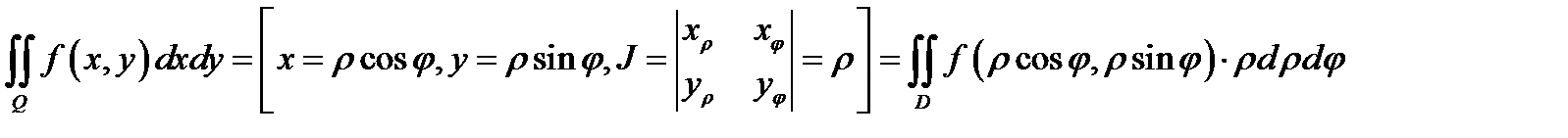
для двойного интеграла в полярных координатах. Здесь и выше 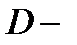область, которая при отображении 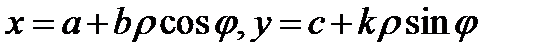переходит в область

Дата добавления: 2018-04-15; просмотров: 417; Мы поможем в написании вашей работы!
Поделиться с друзьями:

12 3 4 5 6 7 8 Следующая ⇒

Мы поможем в написании ваших работ!