Тройные интегралы: определение, условия существования, основные свойства, сведение к повторным интегралам. (ВОПРОС 3)
Определение: Тройным интегралом от функции f(x, y, z) по области V называется конечный предел трехмерной интегральной суммы при стремлении к нулю ранга разбиения, порождающего эту сумму (если этот предел существует и не зависит ни от способа разбиения области V на элементарные части, ни от выбора точек на каждой из этих элементарных частей): 
Условия существования: Если функция f (x,y,z) непрерывная в замкнутой области V, то 
существует.
Основные свойства: 1. (линейность) Если функции 
интегрируемы в 
, то и любая их линейная комбинация 
также интегрируема в , причем имеет место равенство
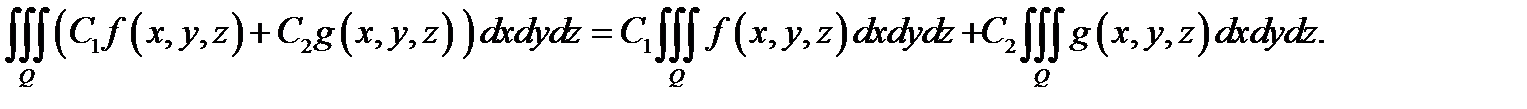
2. (аддитивность) .Если область 
разбита на две непересекающиеся подобласти 
и 
с помощью непрерывной поверхности и если функция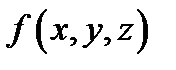 
интегрируема в , то она интегрируема и в каждой из областей и (и наоборот). При этом имеет место равенство 
3. (монотонность).Если функции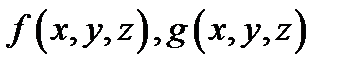 
интегрируемы в 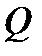и имеет место неравенство 
то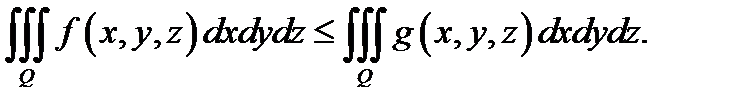 
4. Если функция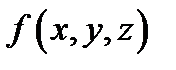 
интегрируема в 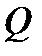и имеют место неравенства 
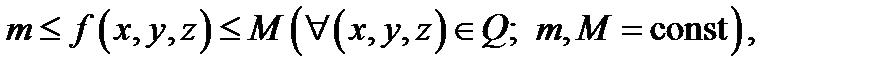то 
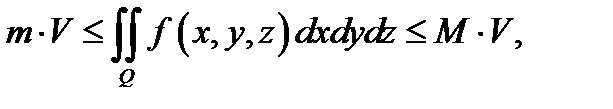где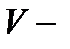 
объём области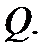 
5. (теорема о среднем) Если функция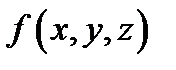 
непрерывна в замкнутой ограниченной области 
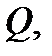то существует точка 
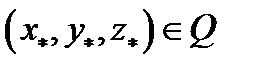такая, что 
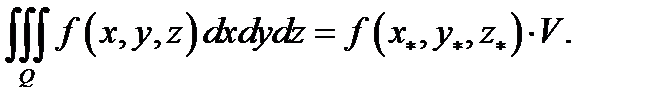И, наконец, отметим, что любая непрерывная и кусочно непрерывная в замкнутой ограниченной (кубируемой) области 
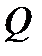функция интегрируема в 
6. 
Теорема 1(Фубини).Если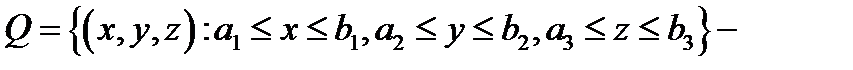 
параллелепипед и если функция 
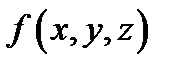кусочно непрерывна в 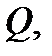то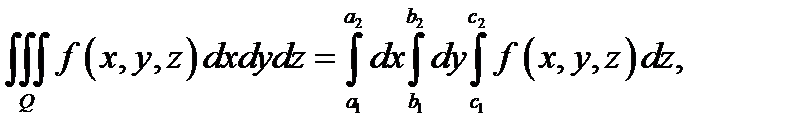 
причем здесь порядок интегрирования может быть изменён как-угодно.
|
|
|
7. Теорема 2(вычисление тройного интеграла в криволинейной области). Если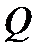 
имеет вид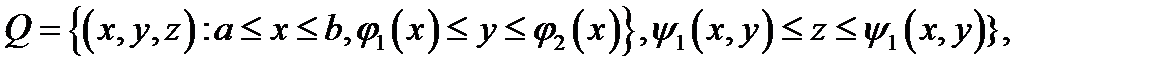 
где функции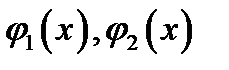 
непрерывны на отрезке 
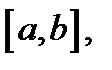а функции 
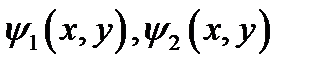непрерывны в области 
и если функция 
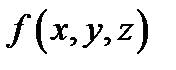непрерывна в 
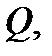то
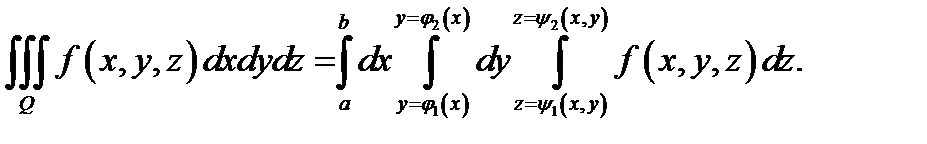
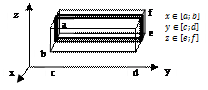
Сведение тройного интеграла к повторному.
Пусть тело V – прямоугольный параллелепипед. Проведём секущую плоскость. Возьмём приращение плоскости (жирные линии). Тогда: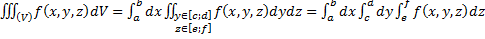 
Рассмотрим 2-й случай: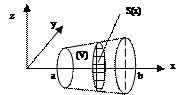 
,тогда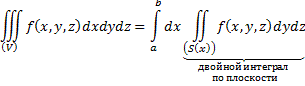 
Третий случай, когда область (V) цилиндрического типа.
.
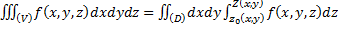Замена переменных в тройных интегралах. Якобиан и его геометрический смысл. Переход к цилиндрическим и сферическим координатам. (ВОПРОС 4)
Если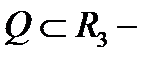 
область переменных 
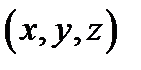, заданных в прямоугольных декартовых координатах, то упорядоченная тройка чисел 
, связанная с предыдущей тройкой равенствами
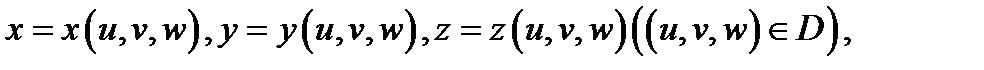
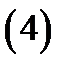
осуществляющими взаимно однозначное отображение области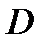 
на область 
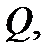называется
криволинейными координатами точки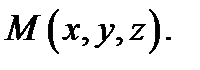 
При этом поверхности
называются координатными поверхностями точки 
(пересечением именно этих поверхностей является точка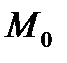 
). Определитель 
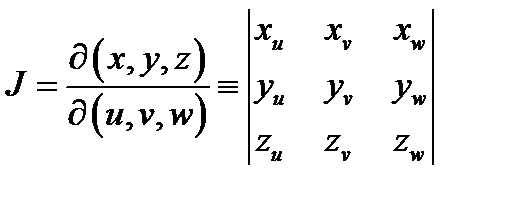называется якобианом отображения (4) или якобианом перехода от декартовых координат к криволинейным. Его геометрический смысл состоит в следующем: 
есть коэффициент искажения объёма малого параллелепипеда с вершиной в точке 
и рёбрами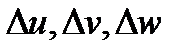 
при отображении (4), т.е. 
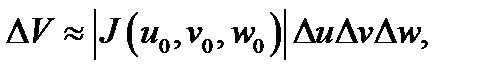где 
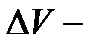объём образа указанного параллелепипеда при отображении (4).Теорема 2. Имеет место равенство
|
|
|
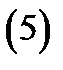
если выполняются следующие условия:
1) функция 
непрерывна в замкнутой ограниченной области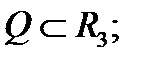 
2) функции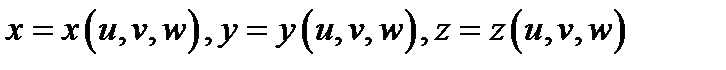 
непрерывно дифференцируемы в области 
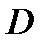и взаимно однозначно отображают область 
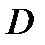на область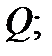 
3) 
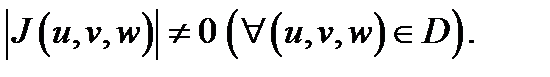
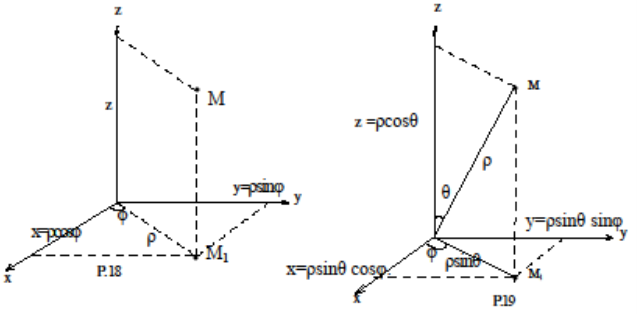
Цилиндрическими координатами называются координаты 
точки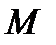 
, связанные с декартовыми координатами 
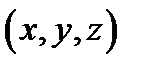этой точки равенствами
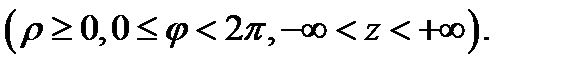(Рис.18)
Нетрудно подсчитать, что якобиан перехода от декартовых координат к цилиндрическим будет равен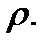 
Действительно, имеем
Следовательно, тройной интеграл в цилиндрических координатах запишется так (см. (5)):
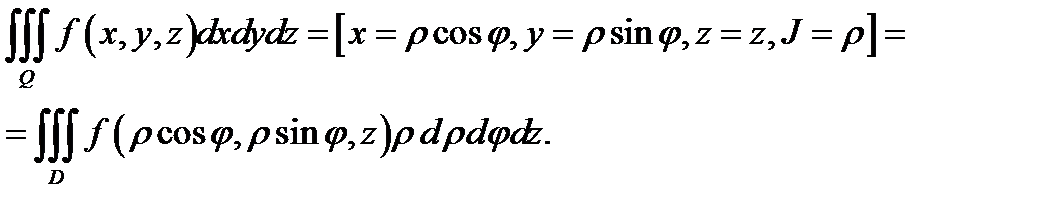
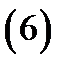
Здесь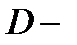 
область, которая при отображении 
переходит в область 
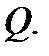
Сферическими координатами называются координаты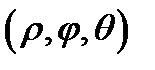 
точки 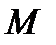, связанные с декартовыми координатами 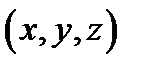этой точки равенствами (Рис.19) 
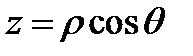
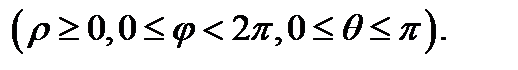Нетрудно показать, что якобиан перехода от декартовых координат к сферическим равен 
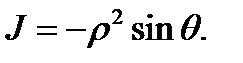Используя теорему 2, запишем тройной интеграл в сферических координатах в виде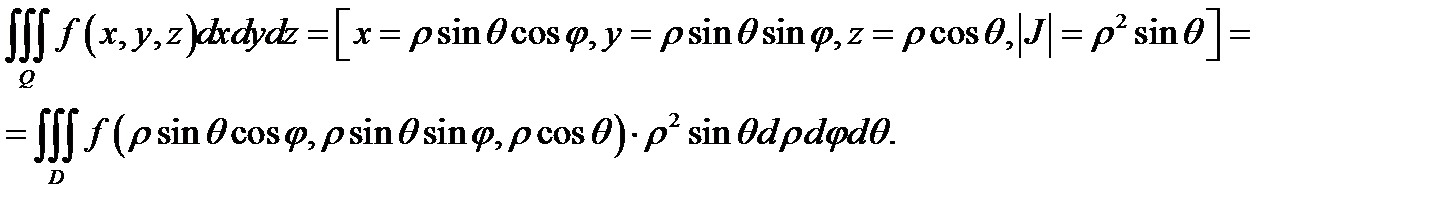 
|
|
|
Здесь 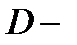область, которая при отображении 
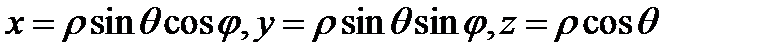переходит в область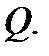
Дата добавления: 2018-04-15; просмотров: 544; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!