Задание 1. Разработайте схемы алгоритмов интерполирования функций по методам Лагранжа, Ньютона, наименьших квадратов
Задание 2. Произведите интерполирование и аппроксимацию табличных функций, приведенных в таблице 3.1 (в соответствии со своим вариантом), на отрезке [a; b] с шагом h средствами MS Excel и MathCad. Средствами Delphi создайте приложение, решающее аналогичную задачу.
Произведите интерполирование и аппроксимацию табличных функций на отрезке [a; b] с шагом h средствами MS Excel. По результатам выполнения постройте графики функций.
Пример выполнения задания
Для функции, заданной таблицей, постройте интерполяционные многочлены Лагранжа и Ньютона. Используя полученные многочлены, вычислите приближенное значение функции на отрезке [–3,25; –1] с шагом 0,25 (табл. 3.2).
Таблица 3.2 – Данные для вычисления приближенного значения функции
| x | –4 | –3 | –2 | –1 |
| y | –3 | –1 | 0 | 7 |
2.1.1 Введите исходные данные и вычислите многочлен Лагранжа для значений указанного отрезка (рис. 3.1). Для этого:
а) введите в ячейку В16 формулу
=$B$4*((A16–$A$5)*(A16–$A$6)*(A16–$A$7))/(($A$4–$A$5)*($A$4–$A$6)*($A$4–$A$7))+$B$5*((A16–$A$4)*(A16–$A$6)*(A16–$A$7))/(($A$5–$A$4)*($A$5–$A$6)*($A$5–$A$7))+$B$6*((A16–$A$4)*(A16–$A$5)*(A16–$A$7))/(($A$6–$A$4)*($A$6–$A$5)*($A$6–$A$7))+$B$7*((A16–$A$4)*(A16–$A$5)*(A16–$A$6))/(($A$7–$A$4)*($A$7–$A$5)*($A$7–$A$6));
б) далее копируйте ее на блок В17: В25;
Рисунок 3.1 – Вычисление многочлена Лагранжа в среде Excel
в) таким образом, в точке x0= –3,25 приближенное значение функции, вычисленное с помощью многочлена Лагранжа равно f(x)= –1,13281;
|
|
|
г) по полученным данным стройте точечные графики функций (рис. 3.2).
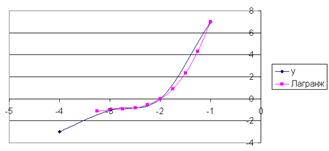
Рисунок 3.2 – Графики исходной и найденной по методу Лагранжа функций
2.1.2. Для построения интерполяционного многочлена Ньютона:
а) скопируйте исходные данные на новый лист Exсel и сделайте пояснительные записки;
б) введите разделенные разности первого порядка в ячейки С5:С7 (см. формулы 3.5), разделенные разности второго и третьего порядков (см. формулы 3.6) соответственно в ячейки D5:D6 и E5 (рис. 3.3);
Рисунок 3.3 – Вид формул для вычисления разделенных разностей в Excel
в) далее получите значения х на заданном интервале, введя следующие формулы в ячейки А16 и А17 (рис. 3.4):
Рисунок 3.4 – Вид формул для вычисления значений х на заданном интервале
д) формулу из ячейки А17 скопируйте на блок А18: А25;
е) в ячейку В16 введите формулу интерполяционного многочлена Ньютона:
=$B$5+(A16–$A$5)*$C$5+(A16–$A$5)*(A16–$A$6)*$D$5+(A16-$A$5)*(A16–$A$6)*(A16–$A$7)*$E$5;
ж) скопируйте ее на блок В17:В25. В результате получите числовые значения (рис. 3.5):
Рисунок 3.5 – Вычисление интерполяционного многочлена Ньютона в Excel
з) по полученным данным постройте точечные графики функций (рис. 3.6):
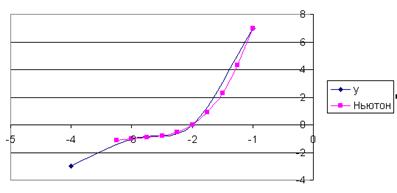
Рисунок 3.6 – Вид построенных графиков функций
|
|
|
и) таким образом, в точке x0= –3,25 приближенное значение функции, вычисленное с помощью многочлена Ньютона равно f(x)= –1,1328125.
2.1.3. Для аппроксимации функции методом наименьших квадратов:
а) скопируйте исходные данные на новый лист Excel;
б) постройте по исходным данным график функции и определите, на какую из стандартных функций он внешне наиболее похож. В рассматриваемом примере график напоминает ветвь параболы, а это значит, что аппроксимационный многочлен будет иметь следующий вид: Рn = a0 + a1x + a2x2 . Следовательно, необходимо найти значения : а0, а1, а2. Для этого проведите вычисления согласно методу наименьших квадратов (рис. 3.7);
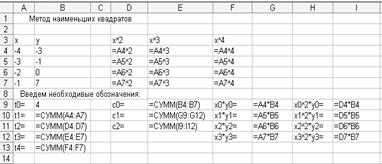
Рисунок 3.7 – Аппроксимация функции методом наименьших квадратов
в) после полученных преобразований создайте систему из трех уравнений, согласно методу наименьших квадратов и решите ее любым известным способом (см. лаб. работу 1). В примере используется метод Гаусса;
г) получив корни уравнения, определите вид многочлена и найдите значения у для заданного интервала х (рис. 3.8).
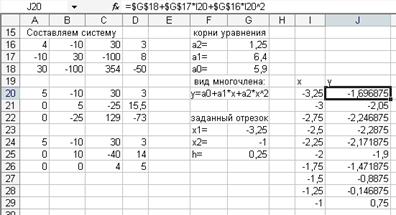
Рисунок 3.8 – Метод наименьших квадратов для вычисления функции на заданном интервале
д) таким образом, в точке x0= –3,25 согласно методу наименьших квадратов приближенное значение функции равно f(x)= –1,696875;
|
|
|
е) постройте точечные графики полученных значений функции методом наименьших квадратов и исходных данных (рис. 3.9).
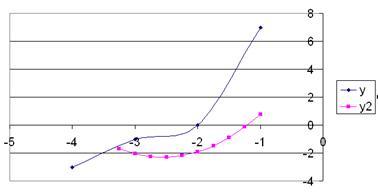
Рисунок 3.9 – Вид построенных графиков функций
Произведите интерполирование и аппроксимацию табличных функций на отрезке [a; b] с шагом h средствами MathCad.
2.2.1. В MathCad можно найти значения функции у в промежуточных точках с помощью полинома некоторой степени. Для этого используются следующие функции:
regress(vx,vy,k) — возвращает вектор, использующийся функцией interp для нахождения полинома степени k, который наилучшим образом приближает значения x и y данных, хранящихся в векторах vx, vy.
interp(vs,vx,vy,x) — возвращает приближенное значение y, соответствующее значению x. Где vs — вектор, получаемый с помощью regress.
Пример выполнения задания
Решите рассматриваемую выше задачу методом наименьших квадратов, а затем с помощью встроенных функций MathCad. Для этого:
а) введите исходные данные:
|
|
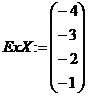
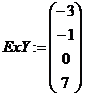
б) так как график исходных точек представляет собой ветвь параболы, то достаточно определить аппроксимирующий полином 2-ой степени. Для этого вычислите коэффициенты системы уравнений:
|
|
|
n := 3 i := 0 .. n t0 := n+1
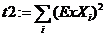
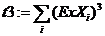
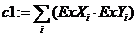
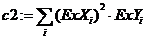
в) определите матрицу коэффициентов и матрицу свободных членов системы:
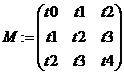
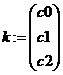
г) найдите коэффициенты полинома, решив систему с помощью функции lsolve(..):
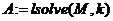
д) определите вид полинома:
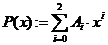
е) укажите количество точек n, значения аргумента хi и его шаг изменения h, для построения графиков функций:
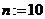
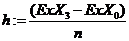
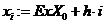
ж) во всех точках хi для сравнения вычислите значения функции с помощью встроенных средств аппроксимации:
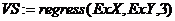
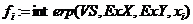
з) постройте графики в соответствии с рисунком 3.10
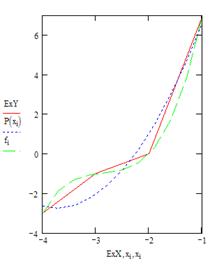
Рисунок 3.10 – Вид графиков в MathCad
2.2.2. В MathCad имеются средства для сплайновой интерполяции.
Интерполирование производится с помощью функции interp(vs,vx,vy,x), которая возвращает вектор значений функции y в интересующих точках х.
Здесь и далее vx — вектор исходных значений аргумента, vy — вектор исходных значений функции, vs — вектор вторых производных, возвращаемых одной из функций cspline(vx,vy), pspline(vx,vy), lspline(vx,vy), которые возвращают вектор vs при использовании кубических, параболических и линейных сплайнов соответственно.
Для интерполирования линиями можно воспользоваться функцией linterp(vx, vy, x).
Пример выполнения задания
Решите рассматриваемый пример (условие см. стр. 45), используя средства MathCad для сплайновой интерполяции. Для этого:
а) введите исходные данные:
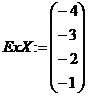
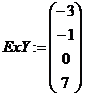
б) определите количество точек n, значения аргумента х и его шаг изменения h, для построения графиков функций:
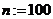
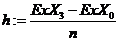
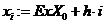
в) во всех точках хi вычислите значения функции с помощью встроенных средств для сплайновой интерполяции:
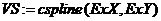
г) постройте графики и выведите значения у в соответствии с рисунком 3.11;
Рисунок 3.11 – Вид графиков интерполирования функций средствами MathCad
2.3. Произведите интерполирование табличных функций методом Лагранжа и Ньютона на отрезке [a, b] с шагом h средствами Delphi.
2.3.1 Расположите на форме основные компоненты (рис. 3.12) согласно рассматриваемому примеру.
Рисунок 3.12 – Вид формы в среде Delphi
2.3.2. Создайте обработчик события нажатием кнопки «Исходные данные», в результате чего в таблице должны появиться исходные числовые данные и на координатной плоскости нарисуется график по данным точкам:
procedure TForm1.Button1Click(Sender: TObject);
var x,y:array[0...3] of real;
i:integer;
begin
stringgrid1.Cells[0,0] := 'X'; stringgrid1.Cells[1,0] := 'Y';
stringgrid1.Cells[0,1] := '–4'; stringgrid1.Cells[1,1] := '–3';
stringgrid1.Cells[0,2] := '–3'; stringgrid1.Cells[1,2] := '–1';
stringgrid1.Cells[0,3] := '–2'; stringgrid1.Cells[1,3] := '0';
stringgrid1.Cells[0,4] := '–1'; stringgrid1.Cells[1,4] := '7';
for i := 0 to 3 do begin
x[i] := strtofloat(stringgrid1.Cells[0,i+1]);
y[i] := strtofloat(stringgrid1.Cells[1,i+1]);
Series1.AddXY(x[i],y[i],'',clTeeColor)
end;
end;
2.3.3. Создайте процедуру-обработчик нажатием кнопки «Лагранж»:
procedure TForm1.Button2Click(Sender: TObject);
var x,y: array[0..3] of real;
i,n,k,j: integer;
P,xn,xk,h,a:real;
begin
xn := strtofloat(edit1.text);
xk := strtofloat(edit2.text);
h := strtofloat(edit3.text);
for i := 0 to 3 do begin
x[i] := strtofloat(stringgrid1.Cells[0,i+1]);
y[i] := strtofloat(stringgrid1.Cells[1,i+1]);
end;
k := 0;
while xn<=xk do begin
P := 0;
for i := 0 to 3 do begin
a := 1;
for j := 0 to 3 do
if i<>j then a := a* (xn – x[j])/(x[i] – x[j]);
P := P+a*y[i];
end;
k := k+1;
stringgrid2.RowCount := k+1;
stringgrid2.Cells[0,k] := floattostr(xn);
stringgrid2.Cells[1,k] := floattostrF(P,ffFixed,6,2);
Series2.AddXY(xn,P,'',clTeeColor);
xn := xn+h;
end;
end;
2.3.4. Создайте алгоритм вычисления промежуточных значений х на интервале [–3,5; –1] методом Ньютона:
procedure TForm1.Button3Click(Sender: TObject);
var x,y: array[0...4] of real;
i,n,k,j,k1: integer;
P,xn,xk,h,a,s1,p1,s,h1:real;
label l;
begin
xn := strtofloat(edit1.text);
xk := strtofloat(edit2.text);
h := strtofloat(edit3.text);
k := 0;
for i := 0 to 3 do begin
x[i] := strtofloat(stringgrid1.Cells[0,i+1]);
y[i] := strtofloat(stringgrid1.Cells[1,i+1]);
end;
while xn<=xk do begin
s := y[0];
for i := 1 to 3 do begin
a := 1; p := 1; s1 := 0;
for j := 0 to i do begin
if i=j then goto l;
p := p*(xn–x[j]);
l: H1 := 1;
for k1 := 0 to i do
begin
if j<>k1 then H1 := H1*(x[j]–x[k1]);
end;
H1 := y[j]/H1; s1 := s1+H1;
end;
p := p*s1;
s := s+p;
end;
k := k+1;
stringgrid3.RowCount := k+1;
stringgrid3.Cells[0,k] := floattostr(xn);
stringgrid3.Cells[1,k] := floattostrF(s,ffFixed,6,2);
Series3.AddXY(xn,S,'',clTeeColor);
xn := xn+h;
end;
end;
2.3.5. Для кнопок «Очистить» и «Выход» создайте процедуры — обработчиков событий самостоятельно.
2.3.6. Запустите проект и протестируйте программу. Полученные результаты вычисления (рис. 3.13).
Рисунок 3.13 – Результаты решения задачи в среде Delphi
Задание 3. Произведите сравнительный анализ полученных результатов. Вычислите среднее квадратичное отклонение метода наименьших квадратов в средах Excel и MathCad. Сделайте вывод.
Таблица 3.1 – Варианты заданий
| Вариант | Значение аргумента x | Значение функции y | Пределы изменения аргумента [a; b] | Шаг интерполирования h |
| 1 | –1,06 –0,837 –0,684 –0,315 –0,117 –0,0 0,115 0,5 | 1,22 0,854 0,513 0,271 0,217 0,198 0,218 0,277 | [–0,8; 0,4] | 0,2 |
| 2 | –2,15 –1,83 –1,62 –1,45 –1,01 –0,72 –0,48 0,0 | –2,23 –2,65 –3,1 –3,54 –4,26 –4,38 –4,52 –4,27 | [–1,95; 0,1] | 0,3 |
| 3 | –0,21 –0,143 –0,099 –0,032 0,114 0,182 0,257 0,38 | –12,64 –11,05 –10,25 –9,32 –9,25 –10,0 –11,48 –14,4 | [–0,2; 0,28] | 0,08 |
| 4 | 0,215 0,441 0,638 0,865 1,05 1,30 1,55 1,82 | 5,82 4,63 4,10 3,34 3,0 3,29 4,32 5,72 | [0,4; 1,6] | 0,2 |
| 5 | –1,0 –0,96 –0,86 –0,79 0,22 0,50 0,93 1,10 | –1,00 –0,151 0,894 0,986 0,895 0,50 –0,306 –0,51 | [–0,98; 1,02] | 0,35 |
| 6 | 0,50 0,75 1,00 1,25 1,50 1,75 2,00 2,25 | 0,1915 0,2734 0,3413 0,3944 0,4332 0,4599 0,4773 0,4878 | [0,625; 2,126] | 0,25 |
| 7 | 1,4 1,6 1,8 2,0 2,2 2,4 2,6 2,8 | –0,24 –0,24 –0,16 0,0 0,24 0,56 0,96 1,44 | [1,5; 2,7] | 0,2 |
| 8 | 0,43 0,48 0,55 0,62 0,70 0,75 0,78 0,81 | 1,64 1,73 1,88 2,03 2,23 2,36 2,41 2,78 | [0,5; 0,6] | 0,02 |
| 9 | 0 15 30 45 60 75 90 105 | 800 718 665 621 586 556 532 510 | [68; 72] | 0,5 |
| 10 | –2,0 3,0 4,5 12,0 15,0 18,5 20,0 23,0 | –17,0 –3,0 1,2 1,8 3,0 4,5 7,0 9,1 | [9,8, 11] | 0,2 |
| 11 | –2,3 0,0 1,1 4,8 7,3 9,2 11,4 13,0 | –12,5 8,6 13,4 15,1 21,4 24,2 28,3 32,1 | [1,5, 3] | 0,5 |
| 12 | 2,34 5,16 7,03 8,42 9,61 10,12 11,35 12,12 | 15,16 25,03 32,18 37,11 44,82 51,62 50,13 73,16 | [3; 6] | 0,5 |
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Аппроксимация и интерполирование функций. Постановка задачи.
2. В чем особенность аппроксимации?
3. Опишите особенности метода наименьших квадратов в случае линейной и квадратичной зависимости.
4. Какой из методов полиномиальной зависимости дает более точный результат в вашем варианте лабораторной работы?
5. Интерполяционный многочлен Лагранжа, его преимущества и недостатки.
6. Интерполяционный многочлен Ньютона, его разновидности.
7. Оценка погрешностей методов.
Тема 4
Численное интегрирование
Постановка задачи.Значение определенного интеграла вычисляется по формуле Ньютона-Лейбница, если удается выразить первообразную формулу через элементарные функции:
, (4.1)
где F(x) — первообразная.
Функция F(x) на отрезке [a; b] называется первообразной функцией f(x), если на всем интервале справедливо равенство F'(x) = f(x).
Однако для большого числа функций первообразная не выражаются через элементарные функции, либо ее сложно определить. Также подынтегральная функция f(x) может быть задана графически или в табличной форме. В таких случаях для вычисления определенного интеграла используют приближенные численные методы.
Суть численных методов вычисления определенного интеграла состоит в замене подынтегральной функции f(x) вспомогательной функцией, интеграл от которой легко вычисляется в элементарных функциях. Наиболее часто подынтегральную функцию f(x) заменяют некоторым интерполяционным многочленом. Это приводит к использованию квадратурных формул:
, (4.2)
где хi — узлы интерполяции;
R — остаточный член (погрешность метода).
В случае отбрасывания R возникает погрешность усечения в процессе вычисления, появляется погрешность округления.
С геометрической точки зрения значение определенного интеграла представляет собой площадь, ограниченную графиком функции y = f(x), осью абсцисс и прямыми x = a, x = b.
Отрезок интегрирования разбивают на n интервалов хi, хi+1, где i = 0,1, ..., n. Приближенно определяются значения площадей, соответствующих каждому отрезку. Их сумма даст приблизительное значение интеграла. В зависимости от способа разбиения отрезка узлами интерполяции хi различают два подхода к построению квадратурных формул:
1. Место положения и длина интервалов разбиения выбираются заранее в начале расчета. В случае равноотстоящих точек узлов интерполирования: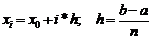 
. В таком случае квадратурные формулы называются формулами Ньютона-Котеса. Они различаются степенями используемых итерационных многочленов. Широкое применение находят формулы трапеции и Симпсона.
2. Место положения и длина интервалов подбираются таким образом, чтобы достичь наибольшей точности (формула Гаусса).
Формула трапеций.Отрезок интегрирования [a;b] разбивают на n равных интервалов длиной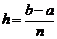 
. В пределах каждого отрезка [хi; хi+1] функция f(x) заменяется интерполяционным многочленом Лагранжа первой степени. Такая замена соответствует замене кривой на секущую (рис. 4.1). Значение
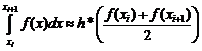. (4.3)
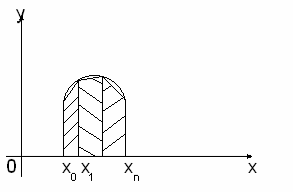
Рисунок 4.1 – Геометрический смысл метода трапеций
Суммирование значений интеграла по всем n участкам разбиения дает общую площадь:
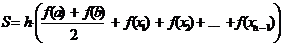. (4.4)
Если функция f(x) на отрезке [a;b] непрерывна и имеет вторую производную, то оценка погрешности усечения находится по формуле:
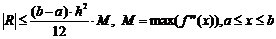, (4.5)
где h — шаг интегрирования;
М — коэффициент, который получается из набора вторых производных для отрезка [a; b].
Очевидно, что формула трапеции (4.4) даст точное значение интеграла для линейной подынтегральной функции f(x).
Формула Симпсона.При замене подынтегральной функции интерполяционным многочленом второй степени и при четном числе n интервалов разбиения квадратурная формула преобразуется к виду:
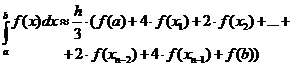(4.6)
— формула Симпсона либо формула параболы.
Значение функции f(x) в нечетных точках разбиения х1, х3 и т. д. входят в формулу с коэффициентом 4. В четных точках х2, х4и т. д. — с коэффициентом 2. В граничных точках х0 и хn — с коэффициентом 1.
Геометрический смысл формулы Симпсона.
Через три последовательные ординаты разбиения проводят параболу и определяют площадь полученной фигуры. Сумму всех фигур, построенных таким образом, дает примерное значение интеграла (рис. 4.2).
Рисунок 4.2 – Геометрический смысл метода Симпсона
При наличии на отрезке [a;b] непрерывной четвертой производной подынтегральной функции оценка усечения формулы Симпсона следующая:
(4.7)
Формула парабол является точной для полиномов третьей степени включительно, так как для них четвертая производная равна 0. Из-за сложности, а часто и невозможности вычисления четвертой производной, используют формулу Рунге:
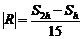, (4.8)
где Sn — значение интеграла при разбиении отрезка интегрирования на n участков (n — четное);
S2n — значение интеграла при разбиении отрезка интегрирования на 2n участков.
Дата добавления: 2018-04-05; просмотров: 1122; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!