Метод деления отрезка пополам

Для применения этого метода функция 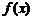 должна быть непрерывна и ограниченанаотрезке AB, внутри которого имеется корень. Значения функции на концах отрезка при этом должны имеют разные знаки  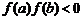(рис. 2.1).

 

 

Рисунок 2.1 – Геометрический смысл метода деления отрезка пополам

Данный метод предусматривает:

1. Отрезок АВ делят пополам и находят начальное приближение корня ;

2. Если , то с — корень уравнения, иначе из отрезков [а; с] и [с; b] выбирают тот, на концах которого функция  имеет разные знаки, и который, следовательно, содержит искомый корень. Выбор интервала сводится к проверке двух условий. Если , то корень расположен на отрезке [а; с] и b := c, если , то корень расположен на отрезке [c; b] и а := с.

3. Найденный интервал, который в большинстве случаев удобно вновь переобозначить как [а; b], вновь делят пополам и выполняют поиск отрезка, содержащего корень и т. д. Если требуется определить корень с точностью ε, то деление пополам продолжают до тех пор, пока длина отрезка не станет меньше 2ε. В этом случае середина последнего отрезка и есть корень с требуемой точностью.

Метод деления отрезка пополам всегда сходится.

Метод касательных (метод Ньютона)

Пусть на отрезке [a; b] имеется корень уравнения 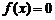. Функция  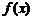на этом отрезке непрерывна, а производные функции  и  определены, непрерывны и сохраняют постоянные знаки. Таким образом, на отрезке [a; b] функция монотонна и не меняет характера выпуклости.

Данный метод предусматривает:

1. Выбирают начальное приближение корня x₀, в качестве которого удобно взять конец отрезка [a; b], для него  (в противном случае сходимость метода Ньютона не гарантируется).

2. Далее проводят касательную в точке C₀ к кривой  до пересечения с осью абсцисс. Абсциссу х₁ принимают за очередное приближение корня (рис. 2.2). Каждое последующее приближение определяется из рекуррентного соотношения

 

.                  (2.2)

 

Рисунок 2.2 – Геометрический смысл метода Ньютона

3. Для оценки расстояния очередного приближения х_k до корня х^* воспользуемся следующими рассуждениями. В соответствии с формулой Лагранжа  получаем, что . О точке с известно лишь то, что она находится между х_k и х*. Поэтому оценка погрешности возможна с помощью следующего соотношения:

,              (2.3)

где .

Метод Ньютона имеет квадратичную сходимость. Иногда, если сложно выбрать начальное приближение, то начинают решение методом деления отрезка пополам (т. е. берут середину отрезка) и продолжают уточнять с помощью метода Ньютона.

Метод хорд

При реализации метода касательных, при каждой итерации нужно вычислять значение как функции 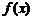, так и ее первой производной. Существует вариант метода Ньютона — метод хорд (секущих), который позволяет избежать вычисления производной. Рекуррентное соотношение для вычисления приближенных значений корня в этом методе имеет вид:

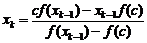.                             (2.4)

В качестве с выбирается конец отрезка (точка а или b), для которого выполняется условие 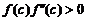. Для начального приближения х₀ выбирается конец отрезка, оставшийся после выбора с (если , то  и наоборот).

Оценка степени приближения к корню производится так же как и при использовании метода касательных.

Название методу было дано из-за его геометрического смысла: если , а , то следующее приближение корня х₁ соответствует точке пересечения хорды, соединяющей концы кривой, с осью абсцисс. Далее на кривой находится точка с абсциссой х₁, проводится следующая хорда и т. д. (рис. 2.3).

 

Рисунок 2.3 – Геометрический смысл метода хорд

 

Этот метод, как и метод касательных, также имеет квадратичную сходимость.

Сравнение методов     

Наибольшей универсальностью обладает метод деления отрезка пополам. С его помощью можно решить любое уравнения вида 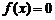, если его корни изолированы, а функция  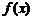на отрезках, содержащих корни, непрерывна. Методы последовательных приближений, касательных и хорд предъявляют к функции более жесткие требования. Сходимость этих методов зависит от выбора начального приближения корня. При реализации этих методов необходимо вычислять производные этих функций для организации итерационного процесса и выполнять проверку условия сходимости.

Методы деления отрезка пополам и последовательных приближений имеют линейную сходимость, а методы касательных и хорд — квадратичную.

При выборе метода уточнения корней нужно помнить, что скорость сходимости и быстрота решения задачи — вещи совершенно разные. Поэтому при привлечении ЭВМ для решения нелинейных уравнений, часто использование более простого метода с малой скоростью сходимости, например, метода деления отрезка пополам может дать результат гораздо быстрее, чем использование изощренного и сложного для понимания и программирования метода уточнения с высокой скоростью сходимости.

 

 

Практикум

Цель работы: изучить различные методы решения нелинейных (и трансцендентных) уравнений; рассмотреть возможности, предоставляемые для решения нелинейных уравнений математическим пакетом MathCad; научиться создавать приложения для решения нелинейных уравнений в среде Delphi.

---

Дата добавления: 2018-04-05; просмотров: 1432; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!