Задание 1. Используя методы Гаусса, простых итераций и Зейделя, разработайте схемы соответствующих алгоритмов решения СЛАУ в среде MS Excel

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ

УЧРЕЖДЕНИЕ ОБРАЗОВАНИЯ «БАРАНОВИЧСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»

Наранович О. И., Раковцы Г. М., Скобля С. Г.

Информатика

Лабораторный практикум

Для студентов II курса специальностей 1-53 01 01 Автоматизация технологических процессов и производств, 1-36 01 03 Технологическое оборудование машиностроительного производства, 1-36 01 01 Технология машиностроения инженерного факультета

Барановичи

РИО БарГУ

2010

УДК 004(076)

ББК 32.81я73

И74

Рекомендовано к печати методической комиссией
инженерного факультета

Разработали

Г. М. Раковцы, О. И. Наранович и С. Г. Скобля

Рецензенты:

Е. Н. Кирюхова, старший преподаватель кафедры
физико-математических дисциплин БарГУ;

О. А. Синдель, инженер-программист ЗАО «АТЛАНТ» БСЗ

И74

Наранович О. И., Раковцы Г. М., Скобля С. Г. Информатика[Текст] : лабораторный практикум / О. И. Наранович, Г. М. Раковцы, С. Г. Скобля. — Барановичи : РИО БарГУ, 2010. — 103 с. — 110 экз. — ISBN 978-985-498-387-5.

Лабораторный практикум посвящен изучению раздела «Численные методы решения инженерных задач» дисциплины «Информатика», содержит пять лабораторных работ с теоретическим материалом и примерами реализации методов в математическом пакете MathCad, а также Excel и Delphi. Издание предназначено для студентов II курса инженерного факультета БарГу.

УДК 004(076)

ББК 32.81я73

ISBN 978-985-498-387-5 © БарГУ, 2010

СОДЕРЖАНИЕ

Лабораторная работа 1. Решение систем линейных уравнений 4

Лабораторная работа 2. Решение нелинейных уравнений 19

Лабораторная работа 3. Аппроксимация и интерполирование функций 40

Лабораторная работа 4. Численное интегрирование 63

Лабораторная работа 5.Численное решение дифференциальных уравнений 75

Литература 80
Введение

Целью настоящего лабораторного практикума является ознакомление студентов с численными методами решения задач. Лабораторные работы нацелены на выработку навыков, необходимых при решении проектных и научных задач с использованием компьютеров.

Первая лабораторная работа, знакомящая с методами решения систем линейных уравнений, отличается невысоким уровнем сложности. При ее выполнении студенты должны познакомиться с такими методами как, метод Гаусса, метод простых итераций и метода Зейделя. Вторая лабораторная работа знакомит студентов с методами решения нелинейных уравнений, таких как метод деления отрезка пополам, метод касательных и метод хорд. В третьей работе представлены задачи аппроксимации и интерполирования функций. Рассмотрены метод наименьших квадратов и методы Ньютона и Лагранжа. Четвертая работа посвящена численному интегрированию и дифференцированию. При ее выполнении студенты должны освоить методы трапеций и Симпсона. Пятая работа знакомит студентов с методами Эйлера и Рунге-Кутта 4 порядка точности решения обыкновенных дифференциальных уравнений.

Практикум включает краткие теоретические сведения по каждой рассматриваемой теме. Теоретический материал излагается сжато и рассчитан на студентов, впервые изучающих данную дисциплину. Приведены примеры решения задач с использованием математического пакета MathCAD, среды программирования Delphi и приложения MS Excel.

Для выполнения практикума студенты должны владеть основами программирования на ЭВМ и иметь навыки работы в математическом пакете MathCAD и приложении MS Excel.

Лабораторный практикум проводится каждым студентом индивидуально. Для этого студент получает одно из заданий по указанному преподавателем варианту.

Практикум считается выполненным после его защиты. Для защиты работы необходимо представить программы, результаты расчета в различных средах и отчёт, оформленный в MS Word, содержащий тему и цель работы, формулировки заданий, формы приложений в Delphi, MS Excel и MathCad, тексты модулей, результаты тестирования приложений, выводы по работе.

Тема 1
Решение систем линейных уравнений

Постановка задачи. Система линейных алгебраических уравнений имеет вид:

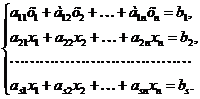(1.1)

Рассмотрим только совместные определенные системы, т. е. системы, имеющие единственное решение. Это ограничение приводит к тому, что число уравнений системы (1.1) должно равняться числу неизвестных.

Используемые в наше время методы решения СЛАУ разбивают на две группы:

1. Точные методы ведутся без округлений и приводят к точным значениям неизвестных. Но так как на практике используемые данные имеют некоторую ограниченную точность, то используемые точные методы решения неизбежно будут давать приближенные значения. К точным методам относится метод Гаусса решения СЛАУ.

2. Приближенные методы при вычислении без округлений позволяют получить решение системы лишь с какой-то заданной точностью. Точное решение системы в этом случае может быть получено теоретически, как результат бесконечного процесса. К приближенным методам решения СЛАУ относят методы простой итерации, метод Зейделя и другие.

Наиболее эффективно программируемыми на ЭВМ являются метод Гаусса с выбором главного элемента в матрице и метод Зейделя. Если при экспериментальных исследованиях получаются приближенные значения коэффициентов СЛАУ, то сначала решают СЛАУ методом Гаусса с выбором главного элемента, а затем уточняют решение методом Зейделя.

Метод Гаусса.Одним из наиболее распространенных методов решения СЛАУ является метод Гаусса.

Суть метода заключается в следующем. Пусть в первом уравнении коэффициент а₁₁ ≠ 0 (если это не так, то на его место можно поставить уравнение, для которого это условие выполняется). Разделим первое уравнение на а₁₁. Затем умножим первое уравнение на а₂₁ и вычтем из второго. Далее умножим первое уравнение на а₃₁ и вычтем из третьего и т. д. В результате получим систему вида:

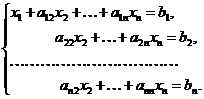(1.2)

Для простоты будем считать, что коэффициенты и свободные члены новой системы мы переобозначили вновь как а и b.

При этом полученная система полностью эквивалентна исходной. Продолжим преобразования. Первое уравнение вообще не будем трогать, а разделим второе уравнение на а₂₂ и будем последовательно вычитать второе уравнение из оставшихся n – 2 - х уравнений, предварительно умножая его на а₃₂, а₄₂ … а_n₂. В результате получим следующую систему:

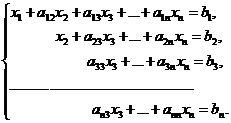(1.3)

Продолжая подобные преобразования, получим систему, приведенную к треугольному виду:

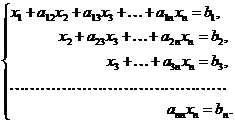(1.4)

Такие преобразования (1.2—1.4) называют прямым ходом метода Гаусса.

Далее из последнего уравнения полученной системы (1.4) выражаем х_n, подставляем в предпоследнее уравнение, затем из него выражаем х_n_{– 1}, подставляем х_n и х_n_{– 1}в предыдущее уравнение и выражаем х_n_{– 2}и т. д. (обратный ход метода Гаусса). В итоге получим набор х₁, х₂… х_n, являющийся решением исходной системы.

Метод Гаусса с выбором главного элемента.При использовании этого метода на первом шаге среди элементов a_i₁ определяют максимальный по модулю элемент. Первое уравнение системы и уравнение, в котором находят максимальный по модулю элемент, меняют местами. Далее стандартным образом (как в методе Гаусса) производят исключения неизвестных х₁. Аналогичные действия повторяют и с оставшимися уравнениями, т. е. из оставшихся n – 1 уравнений на вторую строку переставляют уравнение с максимальным коэффициентом при х₂. Делят второе уравнение на а₂₂ и последовательно вычитают его из оставшихся n – 2 - х уравнений, предварительно умножая на а₃₂, а₄₂ и т. д.

Смысл выбора главного элемента состоит в том, чтобы сделать меньшими коэффициенты при неизвестных в процессе исключения неизвестных и, тем самым, уменьшить погрешность вычислений.

Метод простой итерации решения СЛАУ.Для использования этого метода систему (1.1) нужно привести к следующему виду (называемому нормальным):

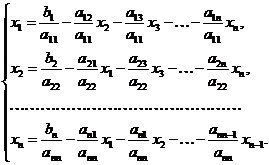(1.5)

Затем в полученную систему (1.5) подставляют начальное приближение решения, т. е. некоторый набор значений 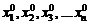и вычисляют следующее приближение решения — набор значений 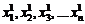. Полученный набор значений снова подставляют в систему (1.5) для вычисления следующего приближения и т. д. Процесс повторяется до тех пор, пока не будет достигнута необходимая точность решения.

Сходимость данного метода определяется выполнением одного из следующих условий:

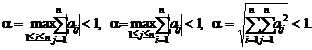(1.6)

Метод простой итерации решения СЛАУ сходится, если максимальная из сумм модулей коэффициентов при неизвестных системы (1.5), взятых по строкам меньше единицы, либо если максимальная из сумм модулей коэффициентов при неизвестных системы (1.5), взятых по столбцам меньше единицы, либо если сумма квадратов всех коэффициентов при неизвестных в правой части системы (1.5) меньше единицы. Каждое из этих условий является достаточным для сходимости метода, но не необходимым. Это означает, что метод сходится при выполнении хотя бы одного из этих условий, но он так же может сходиться и тогда, когда ни одно из них не выполняется.

Момент прекращения вычислений можно определить, руководствуясь эмпирическим правилом: если в ходе итераций десятичная цифра повторилась три и более раз — ее можно считать верной.

Во всех остальных случаях [когда выполняется одно из условий формул (1.6)] степень приближения к точному решению оценивается по формуле

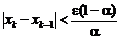, (1.7)

где α— величина, вычисляемая по одной из формул (1.6), по которой обнаружена сходимость метода.

При выполнении одного из условий формул (1.6) в качестве начального значения решения можно взять любой набор значений.

Метод Зейделя решения СЛАУ.Метод Зейделя является модифицированным методом простой итерации.

В данном методе при вычислении k-го приближения неизвестного х_i при i > 1 используются уже вычисленные ранее k-е приближения неизвестных х₁, х₂, … х_i_{– 1}.

Вычислительные формулы при этом примут вид:

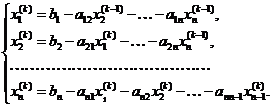(1.8)

Условия сходимости и условия прекращения итераций для метода простой итерации остаются верными и для метода Зейделя.

Обычно метод Зейделя дает более быструю сходимость. Он удобен при программировании, так как при вычислении х_i^k нет необходимости хранить промежуточные значения х₁^k^{– 1}, х₂^k^{– 1}, ... х_n^k^{– 1}.

Практикум

Цель работы: изучить особенности различных методов решения систем линейных алгебраических уравнений (далее — СЛАУ), приобрести навыки решения СЛАУ с помощью средств MS Excel и MathCad.

Задание 1. Используя методы Гаусса, простых итераций и Зейделя, разработайте схемы соответствующих алгоритмов решения СЛАУ в среде MS Excel.

Пример выполнения задания

Найдите решение системы

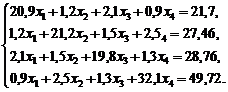(1.9)

1.1. Метод Гаусса в среде MS Excel

1.1.1. В ячейки А2:Е5 введите расширенную матрицу системы (рис. 1.1), скопируйте ее в диапазоны ячеек А7:Е10.

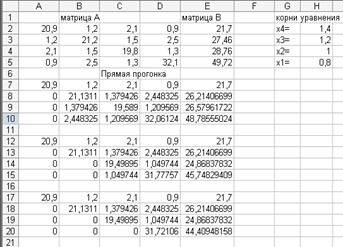
Рисунок 1.1 – Вид решения СЛАУ методом Гаусса в Excel

1.1.2. Прямой ход метода Гаусса:

a)предположите, что в ячейке А2 не ноль. Если это не так, то переставьте строки таким образом, чтобы число в ячейке А2 было отлично от нуля;

б) выделите диапазон А8:Е8 и в строке формул введите формулу

=A3:E3–$A$2:$E$2*A3/$A$2,

нажмите клавиши <Ctrl> + <Shift> + <Enter>. В результате формула примет вид:

{=A3:E3–$A$2:$E$2*A3/$A$2},

где фигурные скобки указывают на операции над матрицами;

в) протянув за маркер автозаполнения, скопируйте формулу в ячейки А9:Е10. В результате этих операций коэффициенты при х₁ во всех уравнениях кроме первого обратятся в ноль;

г) выделите диапазон А7:Е10 и скопируйте значения, хранящиеся в нем в ячейки диапазонов А12:Е15. Для копирования значений нужно воспользоваться специальной вставкой. Ей соответствует пункт меню Правка-Специальная вставка. После выбора этого пункта появляется диалоговое окно Специальная вставка, в котором нужно выбрать Вставить-Значения и нажать ОК;

д) аналогичным образом обратите в ноль коэффициенты при х₂. В диапазон ячеек В14:Е14 введите формулу

=B9:E9–$B$8:$E$8*B9/$B$8,

нажмите клавиши <Ctrl> + <Shift> + <Enter>;

е) протяните маркер автозаполнения этого диапазона так, чтобы заполнить ячейки диапазона В15:Е15. Это обратит в ноль коэффициенты при х₂ в последних двух уравнениях.

ж) далее содержимое (только значения!) диапазона A12:Е15 скопируйте в ячейки диапазона A17:Е20;

з) выделите диапазон С20:Е20, введите в него формулу

{=C15:E15–$C$14:$E$14*C15/$C$14},

что обратит в ноль коэффициент при х₃ в последнем уравнении;

и) в результате этих преобразований матрица системы примет треугольный вид.

1.1.3.Обратный ход метода Гаусса:

а)в ячейки G2, G3, G4 и G5 введите х4, x3, x2 и х1 соответственно, а в ячейки Н2:Н5 — формулы из таблицы 1.1;

Таблица 1.1 — Обратный ход метода Гаусса

Ячейка	Формула
Н2	= E20 / D20
Н3	= (E19 – D19 * H2) / C19
Н4	= (E18 – D18 * H2 – C18 * H3) / B18
Н5	= (E17 – D17H2 – C17 H3 – B17 * H4) / A17

б) в результате чего в диапазоне Н2:Н5 будет получено решение системы (рис. 1.1).

1.2. Метод простых итераций в среде MS Excel:

а) в ячейки А2:Е5 введите расширенную матрицу системы (рис. 1.2) и сделайте пояснительные записи;

б) приведите систему к нормальному виду, т. е. все коэффициенты первого уравнения разделите на а₁₁, все коэффициенты второго уравнения на а₂₂ и т. д. Для этого в диапазон ячеек А8:А11 введите надписи: х1=, х2=, х3=, х4=. Выделите блок ячеек В8:Е8, в строке формул введите формулу =$B$2:$E$2/$A$2 и нажмите клавиши <Ctrl> + <Shift> + <Enter> (операция над матрицей);

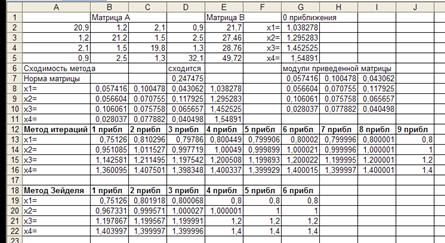
Рисунок 1.2 – Вид решения СЛАУ методом простых итераций и методом Зейделя в Excel

б) в ячейку В9 введите формулу =А3/В3. Далее выделите диапазон ячеек С9:Е9 и введите формулу =С3:Е3/В3, используя операцию над матрицей;

в) в блок ячеек В10:С10 внесите формулу =А4:В4/С4, а в блок D10:E10 — соответственно =D4:E4/C4, используя операцию над матрицами. Для блока В11:D11 введите формулу =А5:С5/D5, а в ячейку Е5 — формулу = E5/D5;

г) из полученной системы определите норму матрицы и признак сходимости метода. Для этого найдите модули полученных коэффициентов и в ячейку G7 введите формулу =ABS(B8), которую скопируйте на блок G7:I10. В ячейке D6 проверьте один из признаков сходимости и введите формулу =ЕСЛИ(МАКС (G7 + G8 + G9 + G10; H7 + H8 + H9 + H10; I7 + I8 + I9 + I10) < 1; "сходится"; "не сходится");

д) в ячейке D7 определите норму матрицы по формуле: =МАКС(G7 + H7 + I7; G8 + H8 + I8; G9 + H9 + I9; G10 + H10 + I10). Если полученный ответ меньше 1, то метод сходится при любых начальных приближениях. За начальное (нулевое) приближение возьмите полученные свободные члены и внесите их в ячейки G2:G5. Вычислим первые приближенные значения: х1(1), х2(1), х3(1), х4(1) по формулам (табл. 1.2);

Таблица 1.2 – Вычисление первых приближенных значений

Ячейка	Формула
В13	= E8 – B8G3 – C8 G4 – D8 * G5
В14	= E9 – B9 * G2 – C9 * G4 – D9 * G5
В15	= E10 – B10 * G2 – C10 * G3 – D10 * G5
В16	= E11 – B11 * G2 – C11 * G3 – D11 * G4

е) таким образом получите первые приближенные значения х1, х2, х3, х4. Далее в ячейки С13:С16 введите формулы, используя уже новые полученные приближения из В13:В16 (табл. 1.3).

Таблица 1.3 – Продолжение вычислений

Ячейка	Формула
С13	= $E$8 – $B$8 * B14 – $C$8 * B15 – $D$8 * B16
С14	= $E$9 – $B$9 * B13 – $C$9 * B15 – $D$9 * B16
С15	= $E$10 – $B$10 * B13 – $C$10 * B14 – $D$10 * B16
С16	= $E$11 – $B$11 * B13 – $C$11 * B14 – $D$11 * B15

ж) используя полученные вторые приближения, скопируйте формулы из ячеек С13:С16 на блок ячеек D13:D16. В результате получите новые приближенные значения корней. Продолжайте операцию копирования, получая новые приближения. Момент прекращения вычислений определите эмпирическим правилом.

1.3.Метод Зейделя в среде MS Excel:

а) в блоке ячеек В19:В22введите формулы вычисления корней уравнения по методу Зейделя (табл. 1.4).

Таблица 1.4 – Вычисление корней уравнения по методу Зейделя

Ячейка	Формула
В19	= $E$8 – $B$8 * G3 – $C$8 * G4 – $D$8 * G5
В20	= $E9 – $B$9 * B19 – $C$9 * G4 – $D$9 * G5
В21	= $E$10 – $B$10 * B19 –$C$10 * B20 – $D$10 * G5
В22	= $E$11 – $B$11 * B19 – $C$11 * B20 – $D$11 * B21

б) рассуждая аналогично, введите формулы в ячейки C19:C22, используя соответственно полученные данные из В19:В22 (табл. 1.5).

Таблица 1.5 – Продолжение вычислений

Ячейка	Формула
С19	=$E$8 – $B$8 * B20 – $C$8 * B21 – $D$8 * B22
С20	=$E$9 – $B$9 * C19 – $C$9 * B21 – $D$9 * B22
С21	=$E$10 – $B$10 * C19 – $C$10 * C20 – $D$10 * B22
С22	=$E$11 – $B$11 * C19 – $C$11 * C20 – $D$11 * C21

в) скопируйте формулы из ячеек С19:С22 на блоки: D19:D22, Е19:Е22 и т.д. Момент прекращения вычислений определяется, как и в методе простых итераций, эмпирическим правилом.

Задание 2. Изучите возможности математического пакета MathCad при решении СЛАУ и разработайте схемы программ решения СЛАУ с использованием средств: lsolve( ), Given … Find( ), метода обратной матрицы и метода Гаусса.

Пример выполнения задания

Используя возможности пакета MathCad,найдите различные способы решения СЛАУ вида:

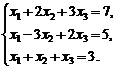(1.10)

2.1. Метод обратной матрицы:

а) установите режим автоматических вычислений, пометив строку Automatic Calculation (Автовычисление в подменю Вычисление) в меню Tools (Инструменты);

б) присвойте переменной ORIGIN значение, равное 1. Значение этой переменной определяет номер первой строки (столбца) матрицы. По умолчанию в Mathcad нумерация начинается с 0.

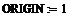в) введите матрицу системы и матрицу-столбец свободных членов, используя инструмент на панели Matrix (или меню Вставить-Матрица):

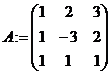
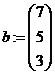
г) вычислите решение системы по формуле ;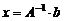

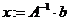
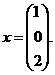
д) проверьте правильность решения умножением матрицы системы на вектор-столбец решения:

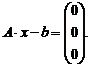
2.2 С помощью функции lsolve():

Повторив пункты2.1,а) — в), перейдите к вычислению корней системы:

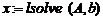
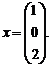
2.3 С помощью функции Given…Find():

а) введите начальные приближения: x1 := 1, x2 := 1, x3 := 1;

б) введите слово Given;

в) ниже введите систему уравнений, используя при этом вместо обычного знака «равно» знак булева равенства (вводится нажатием <Ctrl>+=):

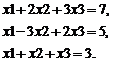
г) ниже напишите: Find(x1,x2,x3)= и получите ответ

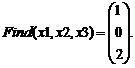
2.4 Метод Гаусса:

а) установите режим автоматических вычислений, пометив строку Automatic Calculation в меню Tools;

б) присвойте переменной ORIGIN значение, равное 1:

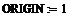
в) введите матрицу системы и матрицу-столбец свободных членов, используя инструмент на панели Matrix:

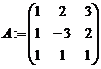
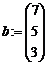
г) сформируйте расширенную матрицу системы, используя функцию augment(A,b), которая формирует матрицу, добавляя к столбцам матрицы системы А справа столбец свободных членов b:

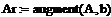
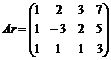
д) приведите расширенную матрицу к ступенчатому виду, используя функцию rref(Ar), которая приводит расширенную матрицу к ступенчатому виду с единичной матрицей в первых столбцах, т. е. выполняет прямой и обратный ходы метода Гаусса:

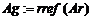
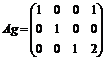
е) сформируйте столбец решения системы, используя функцию submatrix(Ag,1,3,4,4), которая выделяет блок матрицы Ag, расположенный в строках с 1-й по 3-ю и в столбцах с 4-го по 4-й (последний столбец):

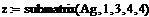
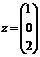
ж) проверьте правильность решения умножением матрицы системы на вектор-столбец решения:

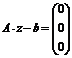
з) полученный результат подтверждает правильность вычислений.

Примечание: в среде MathCad важен порядок расположения операторов, которые выполняются сверху вниз, слева направо.

Дата добавления: 2018-04-05; просмотров: 1968; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 3 4 5 6 7 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!