Задание 1. Разработайте алгоритмы решения нелинейных уравнений методами: деления отрезка пополам, хорд, касательных (Ньютона)
Задание 2. Найдите решения нелинейных уравнений, приведенных в таблице 2.1 (в соответствии со своим вариантом), с использованием функции root(..) математического пакета MathCad.
Для простейших уравнений вида f(x) = 0 решение в Mathcad находится с помощью функции root(..).
Синтаксис:
root( f(х1, x2, …), х1, a, b) — возвращает значение х1, принадлежащее отрезку [a, b], при котором выражение или функция f(х) обращается в 0. Оба аргумента этой функции должны быть скалярами. Функция возвращает скаляр.
Аргументы:
f(х1, x2, …) — функция, определенная где-либо в рабочем документе, или выражение, равное нулю. Выражение должно возвращать скалярные значения.
х1 — имя переменной, которая используется в выражении. Этой переменной перед использованием функции root необходимо присвоить числовое значение. Mathcad использует его как начальное приближение при поиске корня.
a, b — границы интервала, в котором лежит корень уравнения. Внутри интервала не должно быть больше одного корня, так как MathCad выводит на экран лишь один корень, лежащий внутри интервала. Эти параметры необязательны, если используются, то должны быть вещественными числами, причем a < b.
Рекомендации по использованию функции root(..):
- для изменения точности, с которой функция root ищет корень, нужно изменить значение системной переменной TOL. Если значение TOL увеличивается, функция root будет сходиться быстрее, но ответ получится менее точен. Если значение TOL уменьшается, то функция root будет сходиться медленнее, но ответ будет более точен. Чтобы изменить значение TOL в определенной точке рабочего документа, используйте определение вида TOL := 0,01. Чтобы изменить значение TOL для всего рабочего документа, выберите команду Инструменты Þ Свойства таблицы… Þ Переменные Þ Допуск сходимости (TOL);
|
|
|
- если два корня расположены близко друг от друга, следует уменьшить TOL, чтобы различить их;
- если функция f(x) имеет малый наклон около искомого корня, функция root(f(x), x) может сходиться к значению r, отстоящему от корня достаточно далеко. В таких случаях для нахождения более точного значения корня необходимо уменьшить значение TOL. Другой вариант заключается в замене уравнения f(x) = 0на g(x) = 0:
.
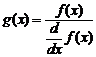Для выражения f(x) с известным корнем а нахождение дополнительных корней f(x) эквивалентно поиску корней уравнения h(x) = f(x) / (x – a). Подобный прием полезен для нахождения корней, расположенных близко друг к другу. Проще искать корень выражения h(x), чем пробовать искать другой корень уравнения f(x) = 0, выбирая различные начальные приближения.
Отсутствие сходимости функции root(..)
Если после многих итераций Mathcad не находит подходящего приближения, то появится сообщение 
(отсутствует сходимость). Эта ошибка может быть вызвана следующими причинами:
|
|
|
- уравнение не имеет корней;
- корни уравнения расположены далеко от начального приближения;
- выражение имеет локальные maxи min между начальным приближением и корнями;
- выражение имеет разрывы между начальными приближениями и корнями;
- выражение имеет комплексный корень, но начальное приближение было вещественным.
Чтобы установить причину ошибки, исследуйте график f(x). Он поможет выяснить наличие корней уравнения f(x) = 0 и, если они есть, определить приблизительно их значения. Чем точнее выбрано начальное приближение корня, тем быстрее будет root сходиться.
Приближенные значения корней (начальные приближения) могут быть:
- известны из физического смысла задачи;
- известны из решения аналогичной задачи при других исходных данных;
- найдены графическим способом.
Наиболее распространен графический способ определения начальных приближений.
Пример выполнения задания
2. 1. Графически отделите корни уравнения
:
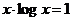а) представьте уравнение в виде: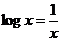 
;
б) постройте графики функций, определив их вид заранее (рис. 2.4):
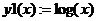
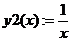
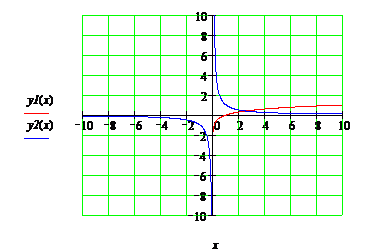
Рисунок 2.4 – Вид графиков в среде MathCad
|
|
|
в) корень найдите по графику, увеличив масштаб (рис. 2.5). Точка пересечения двух графиков и будет искомым корнем уравнения. Для этого:
- выделите график, щелкнув левой кнопкой мыши внутри графика;
- в главном меню MathCad выберите команду Формат — Графики — Масштаб (Format-Graph-Zoom);
- при нажатой левой кнопке мыши обведите пунктирной линией область графика вблизи искомого корня, которую надо увеличить;
- в открытом окне Масштаб по осям Х-У (Х-У Zoom) нажмите кнопку Zoom;
г) прямо с графика передайте в буфер обмена численное значение корня. Для этого выполните следующие действия:
- выделите график, щелкнув левой кнопкой мыши внутри него;
- в главном меню выберите команду: Формат-Графики-Трассирование (Format-Graph-Trace) (рис. 2.5);
- после щелчка левой кнопкой мыши внутри графика появится перекрестье осей, которое с помощью мыши установите на пересечение графиков. При этом численные значения координат перекрестья появляются в открытом окне Х-Y Trace (Трассировка X,Y);
- правильно выбрав положение перекрестья, нажмите кнопки Copy X и Copy Y — численные значения будут помещены в буфер (см. рис. 2.5);
- вне поля графика запишите имя для корня и оператор присваивания :=. Нажмите кнопку Paste (Вставить) в стандартном меню MathCad;
|
|
|
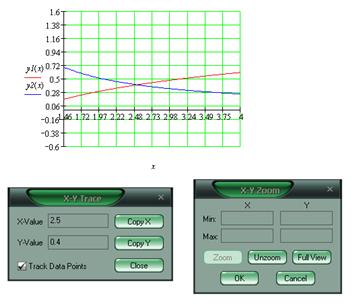
Рисунок 2.5 – Определение корня уравнения
д) приближенно нашли единственный корень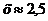 
уравнения 
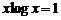и определили его содержащий отрезок [2; 3].
2.2. Уточните корни уравнения 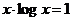с помощью функции root(..):
а) для локализации корней удобно построить график функции. Для этого:
- определите функцию, приравняв ее к нулю, т. е. введите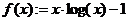 
;
- выберите пункты меню Вставить-Графики-Зависимость XY;
- под осью абсцисс введите х, слева от оси ординат — f(x);
- при необходимости корректируйте пределы изменения аргумента и функции;
б) основные свойства графика можно настроить, выбрав пункт Формат в контекстном меню, вызываемом щелчком правой кнопкой мыши на графике;
в) в результате анализа графика определите начальные приближения корней уравнения;
г) установите точность вычислений, изменяя значения пункта Порог сложности на закладке Толерантность (Tolerance) окна, вызываемого командой Формат-Результат (Format-Result). На закладке Формат номера того же окна выберите способ отображения результата и количество отображаемых десятичных знаков;
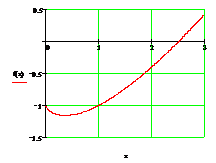д) введите начальное приближение х, которое определите визуально по графику. В данном случае х := 2. Далее введите функцию root(f(x),x)= и получите ответ, который выводится автоматически самой средой (рис. 2.6).
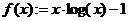
x:=2
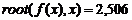
Рисунок 2.6 – Уточнение корня уравнения с помощью функции root(..)
Примечание: в окне Х-Y Trace (Трассировка X,Y) есть пункт Track Data Points (Отмечать расчетные точки). Если установить этот флажок, при перемещении мыши пунктирное перекрестье на графике будет перемещаться скачками, отмечая расчетные значения функции. Если флажок снять, движение перекрестья становиться плавным.
Задание 3. Средствами Delphi создайте приложение для решения нелинейных уравнений, приведенных в таблице 2.1 (в соответствии со своим вариантом). Начальные приближения корней выбирайте из указанных областей.
Пример выполнения задания
Решите нелинейное уравнение вида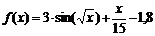 
методами хорд, касательных и делением отрезка пополам.
3.1. Расположите на своей форме основные компоненты среды Delphi, с помощью которых будите решать нелинейное уравнение. Примерный вид формы представлен на рисунке 2.7.
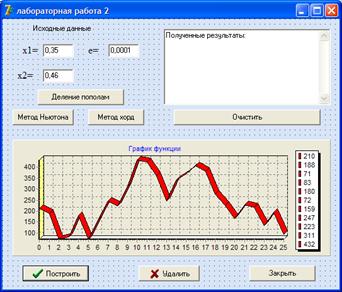
Рисунок 2.7 – Общий вид формы в среде Delphi
3.2. Для каждой кнопки формы создайте процедуры-обработчиков событий, предварительно описав в тексте программы функции, определяющие данное уравнение, первые и вторые производные исходной функции. Для функции вида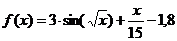 
это выглядит следующим образом:
а) исходная функция опишется следующим образом:
function f(x:real):real;
begin
f := 3*sin(sqrt(x))+x/15–1,8;
end;
б) первая производная опишется так:
function p(x:real):real;
begin
p := (3*cos(sqrt(x)))/(2*sqrt(x))+1/15;
end;
в) вторая производная опишется следующим образом:
function pр(x:real):real;
begin
pр := –3/4*(sin(sqrt(x))/x)–3/4*(cos(sqrt(x))/exp(3/2*ln(x)));
end;
Примечание: часто при нахождении первых и вторых производных сложных функций используются возможности MathCad. Для этого:
а) определите начальную функцию, для данного примера это:
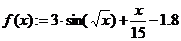
Помните, что в среде MathCad при записи числа целая и дробная часть отделяется точкой;
б) далее введите выражение, используя компонент панели Calculus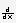 
и Evaluation 
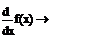
в) отщелкнув кнопкой мыши в сторону, получите вид первой производной;
г) для нахождения второй производной необходимо воспользоваться компонентом панели Calculus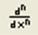 
и Evaluation и выполните следующие действия: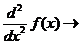 
д) результатом будет вид второй производной:
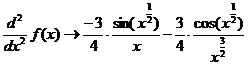
3.3. Текст модуля для нахождения корня методом деления пополам ( кнопка «Деление пополам»):
procedure TForm1.Button1Click(Sender: TObject);
var x1,x2,e,c: real;
begin
e := strtofloat(Edit1.Text);
x1 := strtofloat(Edit2.Text);
x2 := strtofloat(Edit3.Text);
while abs(x2–x1)>e do
begin
c := (x2+x1)/2;
if f(x1)*f(c)<0 then
x2 := c
else x1 := c;
end;
c := (x2+x1)/2;
Memo1.Lines.Add('Корень по методу деления пополам: '+ floattostrf(c,ffgeneral, 5,3));
end;
3.4. Текст модуля для нахождения корня методом касательных (кнопка «Метод Ньютона»):
procedure TForm1.Button2Click(Sender: TObject);
var x1, x2, e, c, d, b, s: real;
begin
e := strtofloat(Edit1.Text);
x1 := strtofloat(Edit2.Text);
x2 := strtofloat(Edit3.Text);
b := x2;
if f(b)*pp(b)<0 then b := x1;
repeat
s := b–f(b)/p(b);
if abs(s)>1
then d := abs((s–b)/s)
else d := abs(s–b);
b := s;
until (d<e);
Memo1.Lines.Add('Корень по методу касательных: '+floattostrf (s, ffgeneral,5,3));
end;
3.5. Модуль для решения уравнения методом хорд (кнопка «Метод хорд»):
procedure TForm1.Button3Click(Sender: TObject);
var s1, x, x0,c,e,x1,x2,:real;
begin
e := strtofloat(Edit1.Text);
x1 := strtofloat(Edit2.Text);
x2 := strtofloat(Edit3.Text);
x := x1;
c := x2;
if f(c)*pp(c)<0 then begin c := x1; x := x2 end;
repeat
x0 := x;
x := (c*f(x0)–x0*f(c))/(f(x0)–f(c));
until abs(f(x))/0,00001<=e;
s1 := x;
Memo1.Lines.Add('Корень по методу хорд:'+floattostrf(s1,ffgeneral, 5,3));
end;
3.6. Модуль для очистки окна Memo (кнопка «Очистить»):
procedure TForm1.Button4Click(Sender: TObject);
begin
Memo1.Clear;
end;
3.7. Текст модуля закрытия приложения (кнопка «Закрыть»):
procedure TForm1.Button5Click(Sender: TObject);
begin
close;
end;
3.8. Модуль для вывода графика (кнопка «Построить»):
procedure TForm1.BitBtn1Click(Sender: TObject);
var x1,x2,x,h,f:real;
begin
x1 := strtofloat(Edit2.Text);
x2 := strtofloat(Edit3.Text);
h := strtofloat(Edit4.Text);
x := x1;
while x<=x2 do
begin
f := 3*sin(sqrt(x))+x/15–1,8;
series1.addXY(x,f);
x := x+h;
end;
end;
3.9. Модуль для удаления графика (кнопка «Удалить»):
procedure TForm1.BitBtn2Click(Sender: TObject);
begin
series1.Clear;
end;
3.10. Запустите приложение и получите корни уравнения разными методами. Сравните результаты.
3.11. Доработайте программу и решите задание согласно своему варианту.
3.12. САМОСТОЯТЕЛЬНО: продумайте, как вычислить погрешности метода хорд и касательных по формуле (2.3). Реализуйте это в своем приложении.
Примечание: погрешность полученных решений не должна превышать ε = 0,0001.
Задание 4. Оцените полученные результаты в Delphi и MathCad, сделайте вывод.
Таблица 2.1 – Варианты заданий
| Вариант | Уравнение | Область, содержащая корень | Методы решения |
| 1 | 2 | 3 | 4 |
| 1 |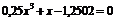 
| [0; 2] | Касательных |
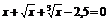
| [0,4; 1] | Деления пополам | |
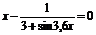
| [0; 0,85] | Хорд | |
| 2 |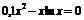 
| [1; 2] | Деления пополам |
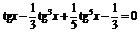
| [0; 0,8] | Хорд | |
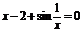
| [1,2; 2] | Касательных | |
| 3 |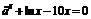 
| [3; 4] | Деления пополам |
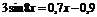
| [-1; 1] | Хорд | |
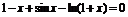
| [0; 1,5] | Касательных | |
| 4 |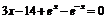 
| [1; 3] | Деления пополам |
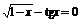
| [0; 1] | Хорд | |
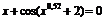
| [0,5; 1] | Касательных | |
| 5 |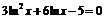 
| [1; 3] | Деления пополам |
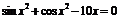
| [0; 1] | Хорд | |
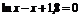
| [2; 3] | Касательных |
Продолжение табл. 2.1
| 6 |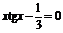 
| [0,2; 1] | Деления пополам |
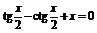
| [1; 2] | Хорд | |
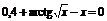
| [1; 2] | Касательных | |
| 7 |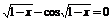 
| [0; 1] | Деления пополам |
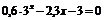
| [2; 3] | Касательных | |
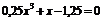
| [0; 2] | Хорд | |
| 8 |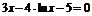 
| [2; 4] | Касательных |
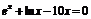
| [3; 4] | Хорд | |
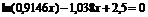
| [1; 6] | Деления пополам | |
| 9 |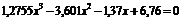 
| [-2; 2] | Деления пополам |
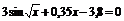
| [2; 3] | Хорд | |
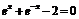
| [0; 1] | Касательных | |
| 10 |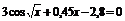 
| [0; 2] | Деления пополам |
|
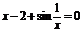
| [1,2; 2] | Хорд | |
|
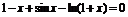
| [0; 1,5] | Касательных | |
| 11 |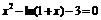 
| [2; 3] | Касательных |
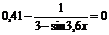
| [0; 0,4] | Хорд | |
|
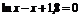
| [2; 3] | Деления пополам | |
| 12 |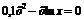 
| [1; 2] | Касательных |
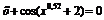
| [0,5; 2] | Хорд | |
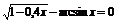
| [0; 1] | Деления пополам |
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Какие методы решения нелинейных алгебраических уравнений вы использовали при выполнении работы?
2. Какой метод отделения корней вы применяли?
3. Опишите алгоритм уточнения корней методом:
а) половинного деления;
б) хорд;
в) касательных (Ньютона).
4. Проведите сравнительный анализ различных методов решения нелинейных уравнений.
5. Назовите способы нахождения начального приближения.
6. Какие аргументы функции root(..) не обязательны?
7. В каких случаях MathCad не может найти корень уравнения?
8. Какая системная переменная отвечает за точность вычислений?
9. Как изменить точность, с которой функция root ищет корень?
10. Как системная переменная TOL влияет на решение уравнения с помощью функции root?
Тема 3
Аппроксимация и интерполирование функций
Постановка задачи.На практике в результате экспериментальных исследований часто получают набор значений некоторой величины у, при фиксированных значениях второй величины x. Аналитическая зависимость между значениями х и у чаще всего неизвестна, что не позволяет, например, вычислить значение величины у в промежуточных точках, отличных от полученных экспериментально. Для нахождения значений в этих промежуточных точках строят приближенную функцию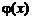 
. Значения функции 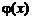в имеющихся точках х либо совпадают, либо приближены к экспериментально наблюдаемым значениям у в этих точках. Построение функции 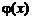называется интерполированием. Таким образом график функции 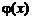должен проходить через все экспериментально полученные точки (хi, yi).
К интерполированию прибегают и в тех случаях, когда аналитический вид некоторой функции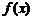 
известен, но получение ее значений в нужных точках требует громоздких вычислений. Чтобы этого избежать, функцию 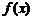также заменяют приближенной функцией .
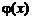В качестве приближенной функции 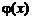часто используется алгебраический многочлен (полином) вида
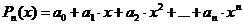. (3.1)
Объясняется это тем, что сравнительно просто автоматизировать вычисления коэффициентов многочлена, легко его интегрировать и дифференцировать. Наряду с многочленами для аппроксимации используют элементарные функции и ряды Фурье.
Интерполяционный многочлен Лагранжа.Интерполяционный многочлен Лагранжа степени n, принимающий в точках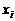 
отрезка [a; b] значения 
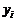, где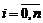 
, имеет вид
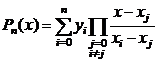(3.2)
или
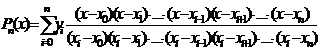. (3.3)
Погрешность интерполяции определяется разностью 
.
Таким образом, значение функции у в точке х, отличной от заданных хi, может быть вычислено по формуле
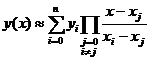. (3.4)
Эту функцию называют функцией Лагранжа.
Интерполяционный многочлен Ньютона.Интерполирование по формуле Лагранжа имеет следующий недостаток: в этой формуле каждое слагаемое представляет собой многочлен n-й степени. Следовательно, при увеличении числа точек хi и, соответственно, yi увеличивается степень многочлена Лагранжа, и так как каждое его слагаемое зависит от всех значений аргумента х, то вычисление полинома Лагранжа необходимо производить заново. Указанного недостатка нет при вычислении полинома Ньютона.
Введем понятие разделенных разностей.
Разделенными разностями 1-го порядка называются значения:
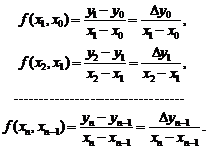(3.5)
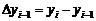— называется конечными разностями 1-го порядка.
Разделенными разностями 2-го и более высоких порядков называют значения:
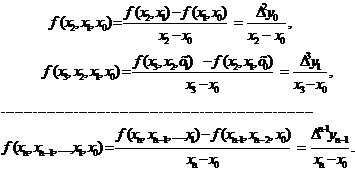(3.6)
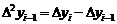— конечная разность 2-го порядка и т. д.
С учетом введенных обозначений интерполяционный многочлен Ньютона имеет вид:
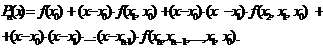(3.7)
Погрешность:
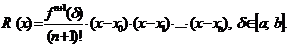(3.8)
Так как любой i-й член полинома Ньютона зависит только от первых i-х точек хi-х и от значения функции в них добавление новых точек вызывает лишь добавление новых слагаемых без изменения первоначальных.
Аппроксимация функций методом наименьших квадратов.Аппроксимация является частным случаем интерполирования и применяется для определения аналитического вида функции, заданной таблично. Задача аппроксимации сводится к определению свободного параметра (параметров) функции заданного вида, который обеспечит наилучшее приближение функции, заданной таблично, модельной аналитической функцией.
Метод наименьших квадратов.
Пусть таблично задана функция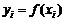 
. Определить аппроксимационный многочлен вида
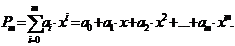(3.9)
Для определения коэффициентов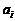 
(где i = 1,2…m) используют аппроксимацию методом наименьших квадратов. Функционал находится по формуле 
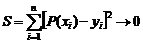, где n — количество пар значений аргумента xi и функции yi. Так как S должен быть минимален, то первые частные производные от S по всем коэффициентам полинома должны равняться нулю.
Вычислим их и приравняем к нулю:
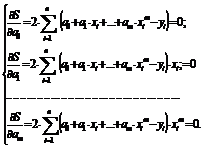(3.10)
После преобразования система слегка упростится:
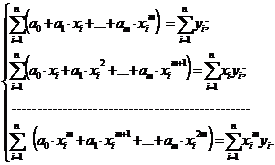(3.11)
Если полином первой степени, то два уравнения, если шестой степени, то семь уравнений. Введем следующие обозначения:
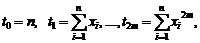
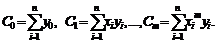(3.12)
С учетом этих обозначений система (3.11) перепишется следующим образом:
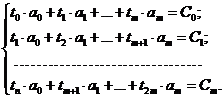(3.13)
Решив эту систему одним из известных методов, определим ряд значений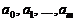 
, с помощью которого и строится многочлен (3.9).
Среднеквадратичное отклонение вычисляется по формуле
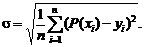(3.14)
Практикум
Цель работы: изучить основные методы интерполирования и аппроксимации функций; научиться использовать для решения задач интерполирования и аппроксимации табличный процессор MS Excel и математический пакет MathCad; научиться создавать приложения для решения задач интерполирования и аппроксимации в среде Delphi.
Дата добавления: 2018-04-05; просмотров: 565; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!