Задание 3. Получите решение СЛАУ, приведенной в таблице 1.5 (в соответствии со своим вариантом), с использованием алгоритмов, полученных при выполнении задания 1 и задания 2

Таблица 1.5 – Варианты заданий

Вариант	Матрица А	Вектор В
1	2	3
1
2
3
4
5
6
7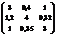
8
9
10
11
12

Задание 4. Вычислите точностные оценки методов по координатам:

где х_i* — значение, найденное методом Гаусса.

Задание 5. На основании полученных результатов проведите сравнительный анализ методов по точности и времени решения, сделайте вывод.

Примечание: погрешность полученных решений не должна превышать ε = 0,0001.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Что называется системой линейных алгебраических уравнений (СЛАУ) и ее решением?

2. Какие системы называются совместными, какие несовместными?

3. Какую систему называют треугольной? Каковы ее особенности?

4. Какие преобразования называют эквивалентными? Приведите пример.

5. Назовите известные Вам методы и средства решения СЛАУ.

6. Объясните сущность метода Гаусса с выбором главного элемента (прямой ход, обратный ход).

7. Каковы сущность и особенности сходимости итерационных методов решения СЛАУ?

8. В чем особенности метода Зейделя (как выбрать начальное приближение, чем обосновать полученное по этому методу решение)?

Тема 2
Решение нелинейных уравнений

Постановка задачи.В практике научных и инженерных расчетов возникает необходимость решения нелинейных уравнений вида 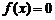. Функция определена и непрерывна на некотором конечном или бесконечном интервалах.

Если функция представляет собой многочлен, то такое уравнение называется алгебраическим.

Если х находится под знаком трансцендентной функции (логарифмическая, показательная, тригонометрическая и т. д.), то в таких случаях уравнение называется трансцендентным.

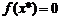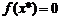Если известно значение x*, при котором выполняется условие , то х* называется корнем уравнения. Такой корень геометрически представляет собой абсциссу точки пересечения (или касания) графика функции с осью Оx. Будем также полагать, что уравнение имеет лишь изолированные корни, т. е. для каждого из корней существует окрестность, не содержащая других корней этого уравнения. В общем случае уравнение не имеет аналитического решения. Так как на практике встречаются уравнения, содержащие коэффициенты с приближенными значениями, то для решения такого уравнения используют численные приближенные методы, которые позволяют определять приближенное значение корней с заданной точностью.

Процесс решения нелинейного уравнения состоит из двух этапов:

1. Этап отделения корней, где производится установление количества корней и поиск интервалов, внутри которых содержится по одному изолированному корню уравнения.

2. Этап уточнения значений корней, на котором значения отдельных корней уточняются одним из известных методов до некоторой заданной степени точности.

Методы отделения корней.Ограничимся рассмотрением методов поиска лишь действительных корней. Существуют два способа отделения корней:

1. Графический способ заключается в обнаружении точек пересечения графика функции с осью Ох. Абсциссы точек пересечения и выбираются в качестве начальных приближенных значений корней.

Часто уравнение 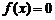можно привести к виду . Тогда отделить корни можно построив графики функций и 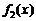и обнаружив точки их пересечения.

2. Численный способ отделения корней основывается на следующем критерии. Если функция 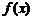непрерывна на отрезке AB и принимает на концах этого отрезка значения противоположных знаков, а производная функции на отрезке AB сохраняет постоянный знак, то внутри отрезка существует корень уравнения, и при этом единственный.

Алгоритм численного отделения корней:

1. Найти производную функции .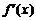

2. Найти критические точки функции .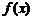

3. Составить таблицу знаков функции 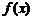на границах отрезка AB и в критических точках.

4. Определить отрезки, на концах которых функция принимает значения противоположных знаков.

5. Выбрать в качестве начальных приближенных значений корней по одному произвольному (если метод уточнения корней, который планируется использовать не налагает каких-либо дополнительных условий) значению х внутри каждого отрезка, найденного в п. 4.

Следует отметить, что универсальных способов отделения корней, пригодных для любых уравнений, не существует.

Приближенные значения корней уточняют различными итерационными методами. Под итерационным методом подразумевается построение числовой последовательности корней, сходящихся к искомому корню х*.

Одной из важнейших характеристик итерационного метода является его скорость сходимости.

Говорят, что последовательность , сходящаяся к пределу х*, имеет порядок сходимости α, если существуют числа и ,такие, что для любого выполняется неравенство

. (2.1)

При сходимость называется линейной, при — квадратичной, а при 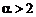— сверхквадратичной. Чем больше порядок сходимости, тем сложнее вычислительный алгоритм, но выше скорость сходимости итерационной последовательности.

Дата добавления: 2018-04-05; просмотров: 363; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 123 4 5 6 7 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!