Построение эмпирической зависимости

Цель работы:

1. Освоить методы построения эмпирических зависимостей для таблично заданных функций.

2. Оценить возможности применения изученных методов при решении практических задач.

3. Приобрести навыки написания программ по имеющимся блок-схемам на одном из изучаемых алгоритмических языков с последующим их оформлением в виде процедур или подпрограмм.

Задание:

1. Для таблично заданной функции в соответствии с вариантом задания (табл. 3.10) построить эмпирическую зависимость в виде квадратичной параболы. Параметры зависимости определить методом наименьших квадратов, используя при решении программу метода Гаусса или Гаусса-Жордана с выбором главного элемента.

2. Составить отчет по работе

Таблица 3.10

№	х₁=0.2	х₂=0.5	х₃=0.7	х₄=1.0	х₅=1.4	х₆=1.6	х₇=1.9	х₈=2.5	х₉=2.6
№	у₁	у₂	у₃	у₄	у₅	у₆	у₇	у₈	у₉
1	2.84	4.25	5.29	7.00	956	10.96	13.21	18.25	19.16
2	368	5.00	6.08	8.00	11.12	12.92	15.92	23.00	24.32
3	452	5.75	6.87	9.00	12.68	14.88	18.63	27.75	29.48
4	536	6.50	7.66	10.00	14.24	16.84	21.34	32.50	34.64
5	3.84	5.25	6.29	8.00	10.56	11.96	14.21	19.25	20.16
6	4.68	6.00	7.08	9.00	12.12	13.92	16.92	24.00	25.32
7	5.52	6.75	7.87	10.00	13.68	15.88	19.63	28.75	30.48
8	6.86	7.50	8.66	11.00	15.24	17.84	22.34	33.50	35.64
9	4.84	6.25	7.29	9.00	11.56	12.96	15.21	20.25	21.16
10	5.68	7.00	8.06	10.00	13.12	14.92	17.92	25.00	26.32
11	6.52	7.75	8.87	11.00	14.68	16.88	20.63	29.75	31.48
12	7.36	8.50	9.66	12.00	16.24	18.84	23.34	34.50	36.64
13	5.84	7.25	8.29	10.00	12.56	13.96	16.21	21.25	22.16
14	6.68	6.00	9.08	11.00	14.12	15.92	18.92	26.00	27.32
15	7.52	8.75	9.87	12.00	15.68	17.88	21.63	30.75	32.48
16	8.36	9.50	10.66	13.00	17.24	19.84	24.34	35.50	37.64
17	6.84	8.25	9.29	11.00	13.56	14.96	17.21	22.25	23.16
18	7.68	9.00	10.08	12.00	15.12	16.92	19.92	27.00	28.32
19	8.52	9.75	10.87	13.00	16.68	18.88	22.63	31.75	33.48
20	9.36	10.50	11.66	14.00	18.24	20.84	25.34	36.50	38.64
21	7.84	9.25	10.29	12.00	14.56	15.96	18.21	23.25	24.16
22	8.68	10.00	11.08	13.00	16.12	17.92	20.92	28.00	29.32
23	9.52	10.75	11.87	14.00	17.68	19.88	23.63	32.75	34.48
24	10.36	11.50	12.66	15.00	19.24	21.84	26.34	37.50	39.64
25	8.84	10.25	11.29	13.00	15.56	16.96	19.21	24.25	25.16
26	9.68	11.00	12.08	14.00	17.12	18.92	21.92	29.00	30.32
27	10.52	11.75	12.87	15.00	18.68	20.88	24.63	33.75	35.48
28	11.36	12.50	13.66	16.00	20.24	22.84	27.34	38.50	40.64
29	9.84	11.25	12.29	1400	16.56	17.96	20.21	25.25	26.16
30	10.68	12.00	13.08	15.00	18.12	19.92	22.92	30.00	31.32

Лабораторная работа 3.10

Численные методы решения задачи Коши

Цель работы:

1. Освоить численные методы решения задачи Коши.

2. Оценить возможности применения изученных методов при решении практических задач.

Задание:

1. По блок-схеме [3, с. 73] составить программу решения задачи Коши методом Эйлера.

2. В соответствии с вариантом задания решить задачу Коши на интервале [0, 0.6] с точностью ε =10^-1 , задавшись начальным числом участков разбиения n = 2. Варианты задания приведены в табл. 3.11.

3. По блок-схеме [3, с. 73] составить программу решения задачи Коши методом Рунге-Кутта.

4. В соответствии с вариантом задания решить задачу Коши на интервале [0, 0.6] с точностью ε =10^-2 , задавшись начальным числом участков разбиения n = 2. Варианты задания приведены в табл. 3.11.

5. Сравнить результаты решения, полученные при использовании методов Эйлера и Рунге-Кутта, и оценить их эффективность.

6. Составить отчет по работе.

Таблица 3.11

№	Исходное уравнение	Начальное условие
1	y^' = 0.1·t² + 2·t ·y	y(t=0) = 0.8
2	y^' =3·t·y - 0.2·y	y(t=0) = 0.5
3	y^' = 2·t·y - 0.2	y(t=0) = 0.3
4	y^' = 0.3·t + y	y(t=0) = 0.4
5	y^' = (0.4 - t²)·y	y(t=0) = 0.7
6	y^' = 0.9·y + 0.1·t	y(t=0) = 0.6
7	y^' = y - 2·t²	y(t=0) = 0.2
8	y^' = 2·t + y	y(t=0) = 0.1
9	y^' = 0.1·t·y + 0.3·y	y(t=0) = 0.9
10	y^' = 3·t·y - 0.1	y(t=0) = 0.4
11	y^' = 0.5·t - y	y(t=0) = 0.2

		Окончание табл. 3.11
№	Исходное уравнение	Начальное условие
12	y^' = y - 2·t	y(t=0) = 0.5
13	y^' = 3·t· - 0.2·y	y(t=0) = 0.2
14	y^' = 0.9·t + 0.1·y	y(t=0) = 0.1
15	y^' = (0.2 - t)·y	y(t=0) = 0.3
16	y^' = 2·t² + y	y(t=0) = 0.4
17	y^' = 0.7·y - 0.1·t	y(t=0) = 0.5
18	y^' =3·t·y + 0.2·t²	y(t=0) = 0.3
19	y^' = 0.1·t + 2·t² ·y	y(t=0) = 0.4
20	y^' = (0.2 + t)·y	y(t=0) = 0.2

Лабораторная работа 3.11

Численное решение краевой задачи

В качестве примера краевой задачи рассматривается задача о прогибе опертой по концам балки, находящейся под нагрузкой. Если балка оперта по концам, то прогиб балки по обоим концам равен нулю.

Дифференциальное уравнение прогибов балки описывается уравнением

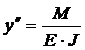где M – изгибающий момент, кг/м;

E – модуль упругости, величина которого зависит от материала балки, кг/см²;

J – момент инерции, величина которого зависит от профиля балки, см⁴.

Исходные данные по материалу и профилю балки представлены в табл. 3.12. Варианты заданий, отличающиеся распределением усилий по длине балки, приведены в табл. 3.13. Значения сосредоточенных усилий и моментов равны Р = 10⁴кг, М =10⁶ кг·см. Положительными являются усилия, направленные вверх, и моменты, направленные по часовой стрелке. Длина балки l = 1 м. Разбиение балки на участки необходимо производить таким образом, чтобы точки приложения сосредоточенных нагрузок совпадали с узлами разбиения, а число участков разбиения было четным.

Пример разбиения балки представлен ниже на рисунке.

Расчет опорных реакций R_Aи R_B

Σ M_A = P·l – P·l/2 – R_B = 0; R_B = 1/2·P;

Σ M_B = P·l/2 + P·l + R_A = 0; R_A = -3/2·P

Цель работы:

1. Освоить методы решения краевой задачи.

2. Оценить возможности применения изученных методов при решении практических задач.

Задание:

1. Рассчитать опорные реакции, исходя из условия равенства нулю суммы изгибающих моментов относительно левого и правого концов балки.

2. Определить формулы для расчета коэффициентов α₀, α₁, β₀, β₁, a_i, b_i, c_i, d_i [3, с. 75].

3. По блок-схеме [3, с. 77] составить программу решения краевой задачи методом «прогонки».

4. В соответствии с вариантом задания решить краевую задачу Коши с точностью ε =10^-1 , задавшись начальным числом участков разбиения n = 4. Для вариантов с нечетными номерами профиль балки – двутавр, для четных вариантов – швеллер. Повторить вычисления для двух моментов инерции и для двух произвольных материалов из табл. 3.12.

5. Составить отчет по работе, содержащий график прогиба балки.

Таблица 3.12

Профиль	J, см⁴	Материал	Е, кг/см²
Двутавр	2·10²	Сталь	2·10⁶
	7·10³	Медь	1.2·10⁶
	2·10⁵	Чугун	1.1·10⁶
Швеллер	2·10¹	Алюминий	0.7·10⁶
	2·10²	Стеклопластик	0.25·10⁶
	2·10³	Древесина	0.1·10⁶

Таблица 3.13

№	Распределение усилий по длине балки
№	x=0.25·l	x=0.5·l	x=0.75·l	x=l
1	Р	-	-Р	-
2	-	М	-Р	-
3	-Р	-	М	-
4	-	Р	-	-М
5	М	-Р	-	-
6	-М	-	-Р	-
7	Р	-Р	-	-
8	Р	-М	-	-
9	-Р	-	-	М
10	-	-М	Р	-
11	-	Р	-Р	-
12	М	-	Р	-
13	М	-М	-	-
14	-	-	М	-М
15	-	-Р	-	М
16	-	М	-М	-
17	Р	-	-	-М
18	-Р	М	-	-
19	-	-	Р	-М
20	-М	-	М	-

Лабораторная работа 3.12

Дата добавления: 2018-04-05; просмотров: 449; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 4 5 6 7 8 9 101112 13 Следующая ⇒

Мы поможем в написании ваших работ!