Оценка центральной тенденции (положения) вариационного ряда. Метод средних величин
· Медиана –это варианта, находящаяся посередине рядараспределения и делящая этот ряд на две равные части по количеству членов. Выбросы, т.е. экстремальные значения, и несимметричные данные оказывают на медиану меньшее влияние, чем на среднюю величину. Поэтому медиану часто используют для описания, например, веса или роста в группах.
· Мода –это величина, представленная наибольшей частотойв ряду распределения. Значение моды легко определяется для категориальных данных. К недостаткам моды является не возможность её алгебраического измерения и игнорирование большой части информации.
· Среднее арифметическое– показатель среднего уровня, самого типичного и характерного для всего ряда.
Получают путь сложения всех значений и деления суммы на число значений в выборке.
Недостатками среднего является искажение данной величины выбросами и асимметричными данными.
Кроме средней арифметической величины твкже различают среднюю геометрическую и среднюю взвешенную.
Значения средней арифметической величины и медианы не обязательно совпадают (рис).

При симметричном распределении значений признака лучшими характеристиками совокупности являются среднее значение и стандартное отклонение, а при несимметричном – медиана и процентили.
Показатели рассеивания
Основными характеристиками рассеивания, применяемых для оценки вариации величин относительно выборочной средней, являются дисперсия, среднее квадратическое отклонение, коэффициент вариации.
|
|
|
· Дисперсия (D, σ2)
o указывает на варьирование, т.е. рассеивание (разброс) исходных данных относительно средней арифметической величины (в квадрате).
o Нелостатком является чувствительность к выбросам. Дисперсия не подходит для асимметрично распределённых данных.
o вычисляется как сумма квадратов разностей эмпирических данных и выборочной средней, делённой на объём выборки:
 или
или 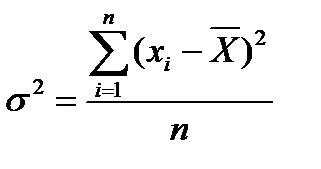
Если n менее 30, то в формуле используется значение (n-1).
· Среднеквадратическое отклонение(σ – сигма) или стандартное отклонение
o характеризует степень отклонения результатов от среднего значения конкретной выборки в абсолютных единицах, является основной мерой изменчивости признака у членов совокупности, имеюшей нормальный тип распределения.
o выражается в тех же единицах, что и варианты ряда.
o может меняться непредсказуемо (расти или уменьшаться с увеличением разброса выборки). Недостатки как и у дисперсии.
o определяется как положительный квадратный корень из дисперсии (поэтому и называется «средним квадратичным отклонением»).
|
|
|

Характеристикой рассеяний является также размах ряда и процентили.
· Стандартная ошибка средней величины (выборки) или ошибка репрезентативности
o Не является описательной статистикой и не должна использоваться в таком качестве.
o Является оценкой возможного отличия между значением среднего в анализируемой выборке и истинным средним во всей популяции (которое на самом деле не может быть определено без анализа бесконечно большого числа наблюдений). Следует использовать для оценки среднего генеральной совокупности.
o Зависит от размера выборки (чем больше размер, тем меньше ошибка репрезентативности).
o Определяется по формуле:
Отличие «m» от «σ»заключается в том, что «σ»характеризует варьирование отдельных вариант вокруг средней величины конкретного вариационного ряда, а «m» – варьирование средних величин отдельных выборок вокруг средней величины генеральной совокупности, т.е. стандартная ошибка отражает точность оценки.
· Коэффициент вариации
o является относительной характеристикой однородности наблюдений.
o определяется как отношение среднего квадратического отклонения к среднему арифметическому, выраженное в процентах:
|
|
|

o В спортивной практике колеблемости результатов измерений в зависимости от величины коэффициента вариации считают небольшой (0-10%), средней (11-20%) и большой (V>20%).
Средняя арифметическое и сигма выражаются в абсолютных единицах и не могут быть использованы для сравнения колеблемости двух и более совокупностей, имеющих различные единицы измерения. Для этого используется коэффициент вариации.
Доверительный интервал (ДИ)
· Диапазон значений (confidence interval, CI), в котором с определённым уровнем надёжности (доверия) содержится истинное популяционное значение параметра (например, среднего). 90%-й доверительный интервал означает, что истинное популяционное значение величины (которое обычно не известно) попадает в рассчитанный интервал с вероятностью 90%. Чем шире доверительный интервал, тем ниже точность оценки. В этом случае ДИ служит описательным целям.
· В биомедицинских исследованиях доверительный интервал среднего обычно устанавливается на уровне 95% и определяется как ± 1,96 стандартной ошибки среднего (коэффициент 1,96 вытекает из предположения нормальности распределения при условии достаточно бальшой выборки). Например, при среднем значении систолического АД в группе равном 125 мм.рт.ст., границы 95% доверительного интервала составляют 115,2 и 134,8 мм.рт.ст. Это значит, что 95% уверенность в том, что истинное среднее значение находится между 115,2 и 134,8 мм.рт.ст. Другими словами 95% ДИ – это 95% доверительный интервал вокруг точечной оценки. 95% - это показатель доверия (доверительная вероятность)
|
|
|
Дата добавления: 2018-04-05; просмотров: 1757; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
