Показатели формы распределения
Существуют различные типы распреления показателей. Однако одним из наиболее важных распределений в статистике является нормальное распределение.
Закон нормального распределения
Нормальное распределение, также называемое Гауссовым распределением, или распределением Гаусса.
Признаки нормального распределения
· Куполообразная симметричная (относительно средней) кривая.
· Распределение характеризуется средней величиной и стандартным отклонением вверх или вниз. При этом, в которое укладываются две трети всех наблюдений (68,3%), отклоняется от средней не более, чем на 1 сигму. В промежутке от плюс 2 сигмы до минус 2 сигмы находится 95,4% наблюдений, а в интервале плюс,минус 3 сигмы - 99,8 % («Правило трёх сигм» - практически все наблюдения укладываются в интервал среднее ± 3 σ).
· Числовые значения средней арифметической, моды и медианы совпадают.
· Сдвигается вправо, если среднее увеличивается, и влево, если среднее уменьшается (при постоянной дисперсии.
· Сплющивается, если дисперсия увеличивается, становится более остроконечной, если дисперсия уменьшается (для постоянного среднего).
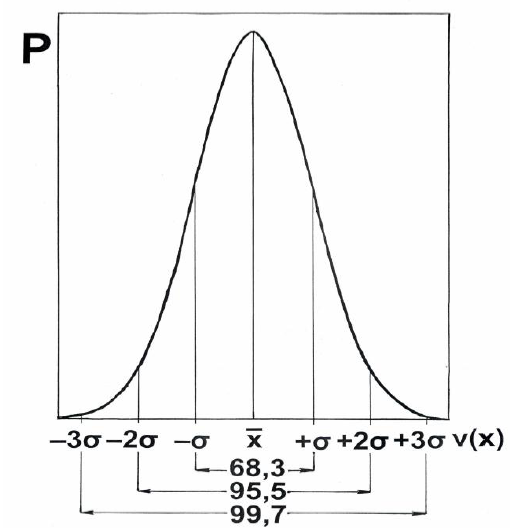
Рис. Кривая нормального распределения
Предположение о нормальности можно проверить, исследуя распределение (например, визуально с помощью гистограммы) или применяя какой-либо критерий нормальности, например, коэффициент асимметрии Пирсона - отношение разности между выборочной средней и модой к среднему квадратическому отклонению:
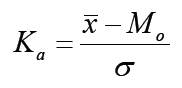

Представление данных
Графическое представление данных
Данные, представленные графически, облегчают визуальное восприятие и анализ информации.
Рекомендации по построению графиков
· График и текст должны взаимно дополнять друг друга.
· График должен быть понятен «сам по себе» и включать все необходимые обозначения (оси, единицы измерения и т.д.).
· На одном графике следует изображать больше четырех кривых.
· Точки на разных линиях принято обозначать кружками, квадратами и треугольниками.
Основные виды графиков
· Столбчатая или колончатая диаграмма (а)
· Круговая диаграмма (б)
· Сегментированная столбчатая диаграмма (в)
· Гистограмма (г) – подобна столбчатой диаграмме, но без пробелов, так как данные непрерывны. Гистаграмма графически изображает частотное распределение.
· Точечный график – каждое индивидуальное значение представлено точкой (д).
· Двумерный график (е) – соотношение между двумя параметрами.
Статистические таблицы
Данные могут быть представлены в виде простых или сложных таблиц. При этом данные могут быть как сгруппированными, так и не сгруппированными (индивидуальными, детализированными). Усложнение таблиц происходит за счет возрастания объема и степени дифференцированности представленной в них информации.
Таблица 1. Динамика гемодинамических показателей студенток специальной медицинской группы с пороками сердца (Х±δ)
| Показатели | Исходные данные | Середина курса | Конец курса |
| ЧСС, уд/мин. | 88,6 ± 2,46 | 80,5 ± 2,5* | 78,0 ± 2,6* |
| САД, мм.рт.ст. | 128,0 ± 2,07 | 115,3 ± 2,0* | 110,8 ± 2,1** |
| ДАД, мм.рт.ст. | 82,5 ± 1,78 | 79,3 ± 1,56 | 71,6 ± 1,24* |
Примечание: * – достоверное изменение по отношению к исходным данным р <0,05; **– достоверное изменение по отношению к исходным данным р < 0,01.
Дата добавления: 2018-04-05; просмотров: 633; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
