Дифференциальные уравнения высших порядков
3.2.1 Дифференциальные уравнения вида 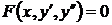
(задание 9)
Найти общее решение дифференциального уравнения второго рода, используя соответствующую замену.
Частным случаем дифференциальных уравнений вида 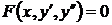 являются уравнения вида
являются уравнения вида 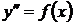 .
.
Для решения необходимо понизить порядок дифференциального уравнения, проинтегрировав правую и левую его части 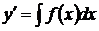 . Полученное уравнение необходимо снова проинтегрировать.
. Полученное уравнение необходимо снова проинтегрировать.
Пример 41
Найти общее решение дифференциального уравнения 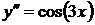 .
.
Решение
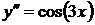 ,
,
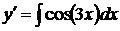 ,
,
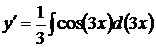 ,
,
 ,
,
 ,
,
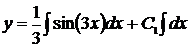 ,
,
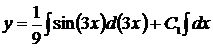 ,
,
 .
.
Дифференциальные уравнения вида 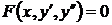 (или вида
(или вида 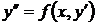 ) решаются с помощью замены
) решаются с помощью замены 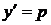 , где
, где 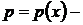 новая неизвестная функция. Тогда
новая неизвестная функция. Тогда 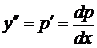 . Исходное уравнение примет вид
. Исходное уравнение примет вид 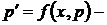 дифференциальное уравнение первого порядка.
дифференциальное уравнение первого порядка.
Пример 42
Найти общее решение дифференциального уравнения 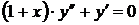 .
.
Решение
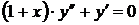 ,
,
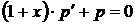 ,
,
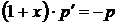 ,
,
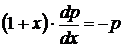 ,
,
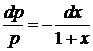 ,
,
 ,
,
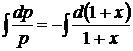 ,
,
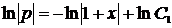 ,
,
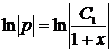 ,
,
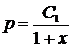 ,
,
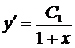 ,
,
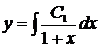 ,
,
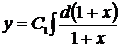 ,
,
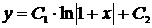 .
.
Пример 43
Найти общее решение дифференциального уравнения  .
.
Решение
 ,
,
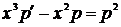 – уравнение Бернулли,
– уравнение Бернулли,
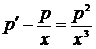 ,
,
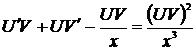 ,
,


 ,
,
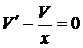 ,
, 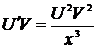 ,
,
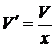 ,
, 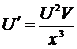 ,
,
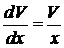 ,
, 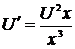 ,
,

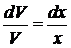 ,
, 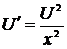 ,
,
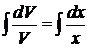 ,
, 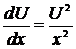 ,
,
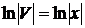 ,
, 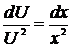 ,
,
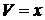 .
. 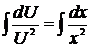 ,
,
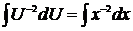 ,
,
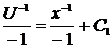 ,
,
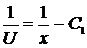 ,
,
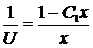 ,
,
|
|
|
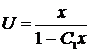 .
.
 |
Так как 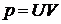 , то общее решение уравнения Бернулли будет иметь вид
, то общее решение уравнения Бернулли будет иметь вид 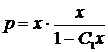 или
или 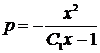 .
.
Заменим 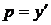 и получим
и получим 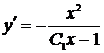 , откуда
, откуда 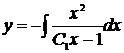 . Найдём этот интеграл отдельно.
. Найдём этот интеграл отдельно.
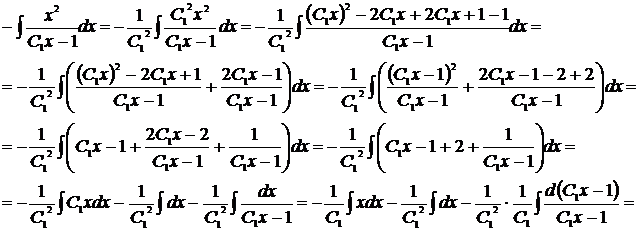
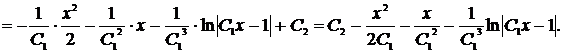
Таким образом, исходное дифференциальное уравнение имеет общее решение 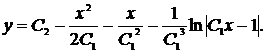
3.2.2 Дифференциальные уравнения вида 
(задание 10)
Найти решение задачи Коши дифференциального уравнения второго рода, используя соответствующую замену.
Дифференциальные уравнения вида  (или вида
(или вида 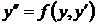 ) решаются с помощью замены
) решаются с помощью замены 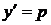 , где
, где 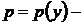 новая неизвестная функция. Тогда
новая неизвестная функция. Тогда 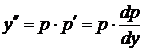 . Исходное уравнение примет вид
. Исходное уравнение примет вид 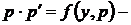 дифференциальное уравнение первого порядка.
дифференциальное уравнение первого порядка.
Пример 44
Найти решение задачи Коши дифференциального уравнения 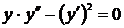 ,
, 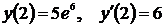 .
.
Решение
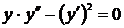 ,
,
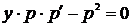 ,
,
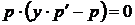 ,
,
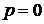 , или
, или 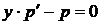 ,
,
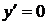 ,
, 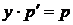 ,
,
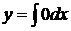 ,
, 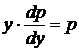 ,
,
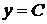 .
. 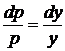 ,
,
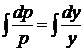 ,
,
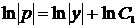 ,
,
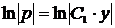 ,
,
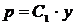 ,
,
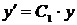 .
.
Можно заметить, что случай 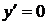 (когда
(когда 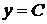 ) является частным случаем дифференциального уравнения
) является частным случаем дифференциального уравнения 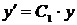 . Таким образом, мы получили одно общее решение исходного дифференциального уравнения. Для упрощения нахождения окончательного ответа, можно на данном этапе воспользоваться дополнительным условием задачи Коши, а именно
. Таким образом, мы получили одно общее решение исходного дифференциального уравнения. Для упрощения нахождения окончательного ответа, можно на данном этапе воспользоваться дополнительным условием задачи Коши, а именно 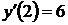 . Подставим в уравнение
. Подставим в уравнение 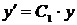 значения
значения 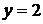 ,
, 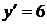 и получим
и получим 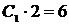 , откуда
, откуда 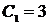 .
.
|
|
|
Теперь, воспользуемся подстановкой 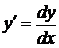 .
.
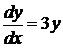 ,
,
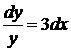 ,
,
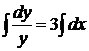 ,
,
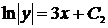 ,
,
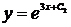 .
.
Заменим 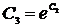 и получим
и получим 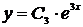 .
.
В полученное уравнение остаётся подставить дополнительное условие задачи Коши 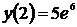 (или
(или 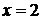 при
при 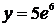 ), то есть получим равенство
), то есть получим равенство 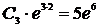 , откуда найдём
, откуда найдём 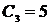 .
.
Итак, частное решение задачи Коши для искомого уравнения имеет вид 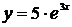 .
.
Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами
(задание 11)
Найти общее решение однородного дифференциального уравнения второго порядка с постоянными коэффициентами.
Дифференциальное уравнение вида 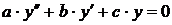 , где
, где 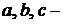 числа (причём
числа (причём 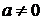 ), называется линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами.
), называется линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами.
Структура общего решения линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами имеет вид
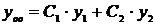 ,
,
где 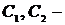 числа, а
числа, а 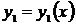 и
и 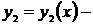 частные решения, образующие фундаментальную систему решений.
частные решения, образующие фундаментальную систему решений.
Фундаментальную систему 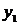 и
и 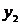 образуют в случае, когда отношение
образуют в случае, когда отношение 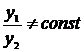 .
.
|
|
|
Эйлером было предложено частное решение искать в виде 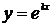 , где
, где 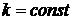 . Тогда
. Тогда 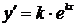 ,
, 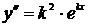 . Подставив
. Подставив 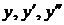 в уравнение
в уравнение 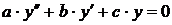 , получим
, получим
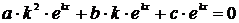 ,
,
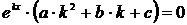 .
.
Из последнего уравнения получим 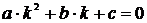 , это равенство называется характеристическим уравнением. В зависимости от корней этого уравнения, общее решение находится тремя способами.
, это равенство называется характеристическим уравнением. В зависимости от корней этого уравнения, общее решение находится тремя способами.
1. Если дискриминант характеристического уравнения 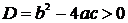 , то уравнение имеет два различных вещественных корня
, то уравнение имеет два различных вещественных корня 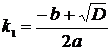 и
и 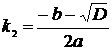 . Тогда общее однородное решение исходного дифференциального уравнения второго порядка с постоянными коэффициентами имеет вид
. Тогда общее однородное решение исходного дифференциального уравнения второго порядка с постоянными коэффициентами имеет вид 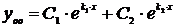 .
.
2. Если дискриминант характеристического уравнения 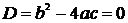 , то уравнение имеет два одинаковых вещественных корня
, то уравнение имеет два одинаковых вещественных корня 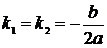 . Тогда общее однородное решение исходного дифференциального уравнения второго порядка с постоянными коэффициентами имеет вид
. Тогда общее однородное решение исходного дифференциального уравнения второго порядка с постоянными коэффициентами имеет вид 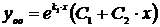 .
.
3. Если дискриминант характеристического уравнения 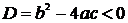 , то уравнение имеет два комплексных корня. Пусть
, то уравнение имеет два комплексных корня. Пусть 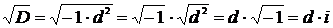 , где
, где 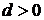 ,
, 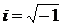 . Тогда корни характеристического уравнения будут равны
. Тогда корни характеристического уравнения будут равны 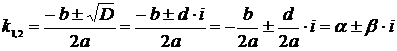 . Общее однородное решение исходного дифференциального уравнения второго порядка с постоянными коэффициентами в этом случае имеет вид
. Общее однородное решение исходного дифференциального уравнения второго порядка с постоянными коэффициентами в этом случае имеет вид 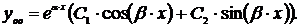
Замечание: характеристическое уравнение можно получать, делая следующие замены 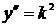 ,
, 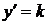 ,
, 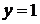 .
.
|
|
|
Пример 45
Найти общее решение однородного дифференциального уравнения второго порядка с постоянными коэффициентами 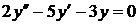 .
.
Решение
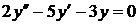 , заменим
, заменим 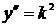 ,
, 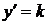 ,
, 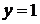 , получим характеристическое уравнение
, получим характеристическое уравнение 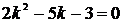 . Дискриминант квадратного уравнения
. Дискриминант квадратного уравнения 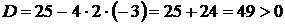 ,
, 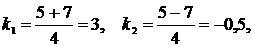 следовательно, получаем случай 1.
следовательно, получаем случай 1.
Тогда общее решение однородного дифференциального уравнения второго порядка с постоянными коэффициентами 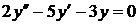 имеет вид
имеет вид 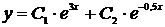 .
.
Пример 46
Найти общее решение однородного дифференциального уравнения второго порядка с постоянными коэффициентами 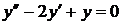 .
.
Решение
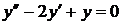 , заменим
, заменим 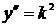 ,
, 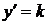 ,
, 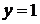 , получим характеристическое уравнение
, получим характеристическое уравнение 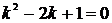 . Дискриминант квадратного уравнения
. Дискриминант квадратного уравнения 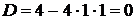 ,
, 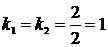 (то есть квадратный трёхчлен является полным квадратом
(то есть квадратный трёхчлен является полным квадратом 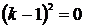 ,
, 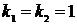 ), следовательно, получаем случай 2
), следовательно, получаем случай 2
Тогда общее решение однородного дифференциального уравнения второго порядка с постоянными коэффициентами 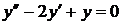 имеет вид
имеет вид 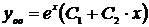 .
.
Пример 47
Найти общее решение однородного дифференциального уравнения второго порядка с постоянными коэффициентами 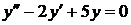 .
.
Решение
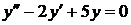 , заменим
, заменим 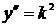 ,
, 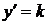 ,
, 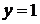 , получим характеристическое уравнение
, получим характеристическое уравнение 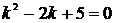 . Дискриминант квадратного уравнения
. Дискриминант квадратного уравнения 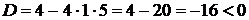 , тогда
, тогда 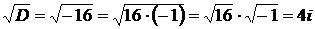 ,
, 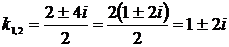 – комплексные корни, следовательно, получаем случай 3
– комплексные корни, следовательно, получаем случай 3 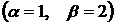 .
.
Тогда общее решение однородного дифференциального уравнения второго порядка с постоянными коэффициентами 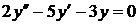 имеет вид
имеет вид 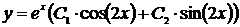 .
.
Пример 48
Найти общее решение однородного дифференциального уравнения второго порядка с постоянными коэффициентами 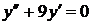 .
.
Решение
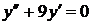 , заменим
, заменим 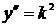 ,
, 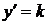 , получим характеристическое уравнение
, получим характеристическое уравнение 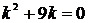 , откуда
, откуда 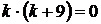 .
.
Решения уравнения 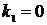 ,
, 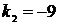 – различные вещественные корни, следовательно, получаем случай 1.
– различные вещественные корни, следовательно, получаем случай 1.
Тогда общее решение однородного дифференциального уравнения второго порядка с постоянными коэффициентами 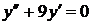 имеет вид
имеет вид 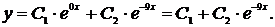
Пример 49
Найти общее решение однородного дифференциального уравнения второго порядка с постоянными коэффициентами 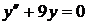 .
.
Решение
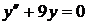 , заменим
, заменим 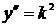 ,
, 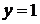 , получим характеристическое уравнение
, получим характеристическое уравнение 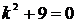 , откуда
, откуда 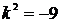 или
или 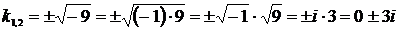 – комплексные корни, следовательно, получаем случай 3.
– комплексные корни, следовательно, получаем случай 3.
Тогда общее решение однородного дифференциального уравнения второго порядка с постоянными коэффициентами 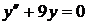 имеет вид
имеет вид 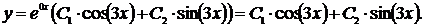
Пример 50
Найти общее решение однородного дифференциального уравнения второго порядка с постоянными коэффициентами 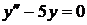 .
.
Решение
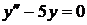 , заменим
, заменим 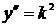 ,
, 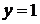 , получим характеристическое уравнение
, получим характеристическое уравнение 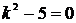 , откуда
, откуда 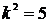 или
или 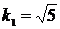 ,
, 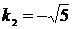 – различные вещественные корни, следовательно, получаем случай 1.
– различные вещественные корни, следовательно, получаем случай 1.
Тогда общее решение однородного дифференциального уравнения второго порядка с постоянными коэффициентами 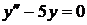 имеет вид
имеет вид 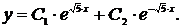
Дата добавления: 2018-04-05; просмотров: 266; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
