Дифференциальные уравнения первого порядка
С разделяющимися переменными
(задание 7)
Найти общее решение дифференциального уравнения с разделяющимися переменными.
Уравнение вида 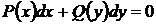 называется уравнением с разделёнными переменными.
называется уравнением с разделёнными переменными.
Решение:
1) Перенесём 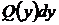 в правую часть уравнения
в правую часть уравнения 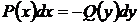 .
.
2) Проинтегрируем левую и правую части уравнения 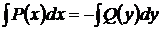 .
.
Пример 35 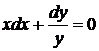
Решение
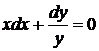 ,
,
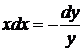 ,
,
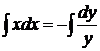 ,
,
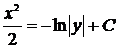 ,
,
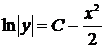 ,
,
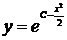 ,
,
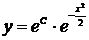 .
.
Заменим 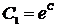 , тогда общее решение исходного дифференциального уравнения имеет вид
, тогда общее решение исходного дифференциального уравнения имеет вид 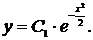
Более общий случай описывают дифференциальные уравнения с разделяющимися переменными, которые имеют вид 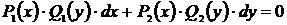 .
.
Решение:
1) Перенесём 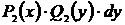 в правую часть уравнения
в правую часть уравнения 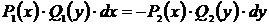 .
.
2) Разделим переменные, используя пропорцию 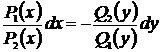 .
.
3) Проинтегрируем левую и правую части уравнения 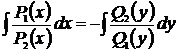 .
.
Пример 36 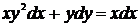
Решение
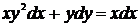 ,
,
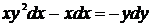 ,
,
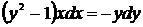 ,
,
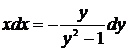 ,
,
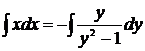 .
.
Интеграл в левой части уравнения является простым табличным, а интеграл, полученный в правой части уравнения, решим отдельно.
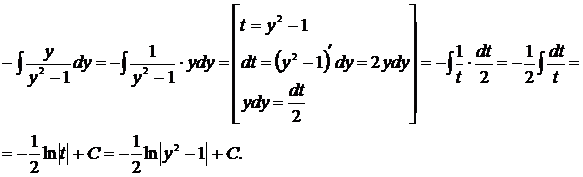
Вернёмся к нашему уравнению: 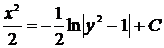 .
.
Заменим 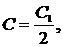 получим
получим 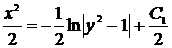 .
.
Таким образом, общее решение исходного дифференциального уравнения имеет вид  .
.
Также уравнение с разделяющимися переменными может иметь вид 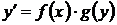 .
.
Решение:
1) Заменим 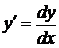 , получим уравнение вида
, получим уравнение вида 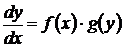 .
.
2) Разделим переменные, используя пропорцию 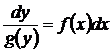 .
.
3) Проинтегрируем левую и правую части уравнения 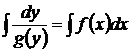 .
.
Пример 37 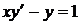
Решение
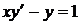 ,
,
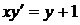 ,
,
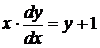 ,
,
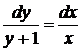 ,
,
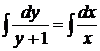 ,
,
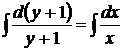 .
.
Замечание: в случае, когда в левой и правой частях дифференциального уравнения интегралы обращаются в логарифмические функции, необходимо прибавлять не постоянную 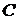 , а постоянную
, а постоянную 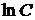 . Это позволяет упростить ответ, воспользовавшись такими свойствами логарифмов, как
. Это позволяет упростить ответ, воспользовавшись такими свойствами логарифмов, как 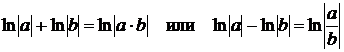 (
( 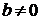 ).
).
|
|
|
Возвращаясь к нашему дифференциальному уравнению, получим
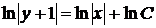 ,
,
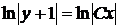 ,
,
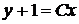 ,
,
Таким образом, общее решение исходного дифференциального уравнения имеет вид 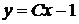 .
.
Линейные дифференциальные уравнения
Первого порядка. Уравнения Бернулли
(задание 8)
Найти решение задачи Коши линейного дифференциального уравнения первого порядка или дифференциального уравнения Бернулли.
Дифференциальное уравнение первого порядка 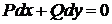 называется линейным, если отношение
называется линейным, если отношение 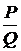 содержит
содержит 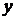 лишь в первой степени (линейно). Линейное уравнение принято записывать в виде
лишь в первой степени (линейно). Линейное уравнение принято записывать в виде 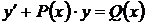 .
.
Решение:
1) Воспользуемся подстановкой 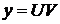 ,
, 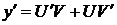 . Получим уравнение вида
. Получим уравнение вида 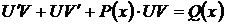 .
.
2) Первое слагаемое 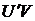 переписываем, а из второго и третьего выносим общий множитель
переписываем, а из второго и третьего выносим общий множитель 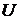 за скобки, то есть получим равенство
за скобки, то есть получим равенство 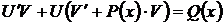 .
.
3) Обнуляем скобку, получая при этом новое дифференциальное уравнение с разделяющимися переменными вида 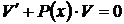 , из которого находим неизвестную переменную
, из которого находим неизвестную переменную 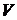 (используя замену
(используя замену 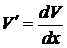 ). Замечание: постоянную
). Замечание: постоянную 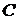 принимаем за ноль!
принимаем за ноль!
4) В уравнение из пункта 2), заменяя выражение 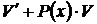 нулём, получим уравнение вида
нулём, получим уравнение вида 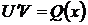 . Подставляя в него значение
. Подставляя в него значение 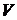 , найденное в пункте 3) и замену
, найденное в пункте 3) и замену 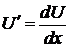 , находим неизвестную переменную
, находим неизвестную переменную 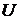 . Замечание: постоянную
. Замечание: постоянную 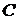 писать обязательно!
писать обязательно!
|
|
|
5) Общее решение линейного дифференциального уравнения первого порядка находится путём подстановки в 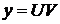 значения переменных
значения переменных 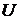 и
и 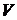 , найденные в пунктах 4) и 3) соответственно.
, найденные в пунктах 4) и 3) соответственно.
Замечание: если в задании имеется дополнительное условие вида 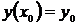 (задача Коши), то может быть найдено частное решение, удовлетворяющее данному условию. Для его нахождения достаточно подставить в общее решение замены
(задача Коши), то может быть найдено частное решение, удовлетворяющее данному условию. Для его нахождения достаточно подставить в общее решение замены 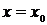 ,
, 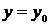 , после чего найти конкретное значение постоянной
, после чего найти конкретное значение постоянной 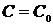 . Подставляя это значение в общее решение дифференциального уравнения, получаем искомое частное решение.
. Подставляя это значение в общее решение дифференциального уравнения, получаем искомое частное решение.
Пример 38
Найти решение задачи Коши 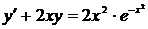 ,
, 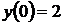 .
.
Решение
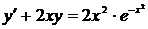 ,
,
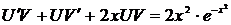 ,
,
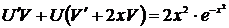 ,
,


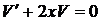 ,
, 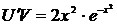 ,
,
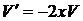 ,
, 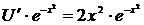 ,
,
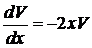 ,
, 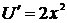 ,
,
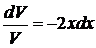 ,
, 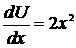 ,
,
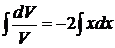 ,
, 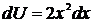 ,
,
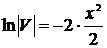 ,
, 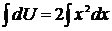 ,
,
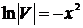 ,
, 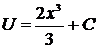 .
.
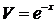 .
.
 |
Так как 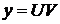 , то общее решение дифференциального уравнения будет иметь вид
, то общее решение дифференциального уравнения будет иметь вид 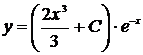 . Найдём теперь частное решение, используя дополнительное условие
. Найдём теперь частное решение, используя дополнительное условие 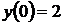 . Подставим
. Подставим 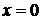 и
и 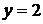 в общее решение, получим
в общее решение, получим 
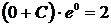 , откуда найдём
, откуда найдём 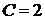 . Тогда частное решение задачи Коши будет иметь вид
. Тогда частное решение задачи Коши будет иметь вид 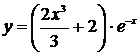 .
.
|
|
|
Линейное дифференциальное уравнение первого порядка также может иметь вид 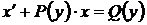 . Решение аналогично, только подстановка в этом случае следующая
. Решение аналогично, только подстановка в этом случае следующая 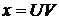 ,
, 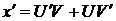 , где
, где 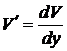 ,
, 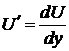 .
.
Пример 39
Найти решение задачи Коши 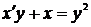 ,
, 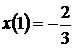 .
.
Решение
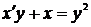 ,
,
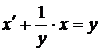 ,
,
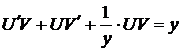 ,
,
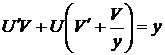 ,
,


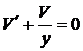 ,
, 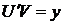 ,
,
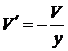 ,
, 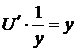 ,
,
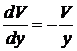 ,
, 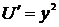 ,
,
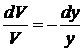 ,
, 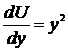 ,
,
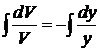 ,
, 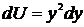 ,
,
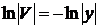 ,
, 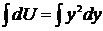 ,
,
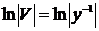 ,
, 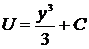 .
.
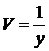 .
.
 |
Так как 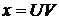 , то общее решение дифференциального уравнения будет иметь вид
, то общее решение дифференциального уравнения будет иметь вид 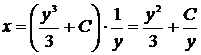 . Найдём теперь частное решение, используя дополнительное условие
. Найдём теперь частное решение, используя дополнительное условие 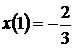 . Подставим
. Подставим 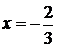 и
и 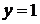 в общее решение, получим
в общее решение, получим 
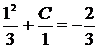 , откуда найдём
, откуда найдём 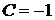 . Тогда частное решение задачи Коши будет иметь вид
. Тогда частное решение задачи Коши будет иметь вид 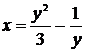 .
.
Дифференциальное уравнение вида 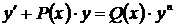 (или
(или 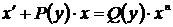 ), где
), где 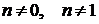 , называется уравнением Бернулли. Схема решения уравнений Бернулли аналогична решению линейных дифференциальных уравнений первого порядка.
, называется уравнением Бернулли. Схема решения уравнений Бернулли аналогична решению линейных дифференциальных уравнений первого порядка.
Пример 40
Найти решение задачи Коши 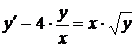 ,
, 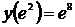 .
.
Решение
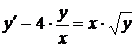 ,
,
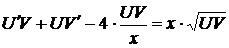 ,
,
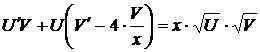 ,
,


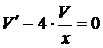 ,
, 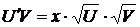 ,
,
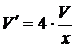 ,
, 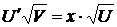 ,
,
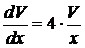 ,
, 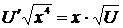 ,
,
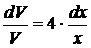 ,
, 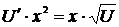 ,
,
|
|
|
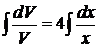 ,
, 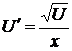 ,
,
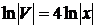 ,
, 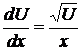 ,
,
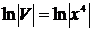 ,
, 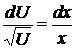 ,
,
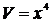 .
. 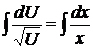 ,
,

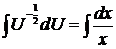 ,
,
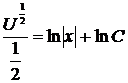 ,
,
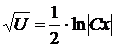 ,
,
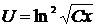 .
.
 |
Так как 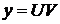 , то общее решение дифференциального уравнения будет иметь вид
, то общее решение дифференциального уравнения будет иметь вид 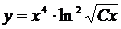 . Найдём теперь частное решение, используя дополнительное условие
. Найдём теперь частное решение, используя дополнительное условие 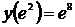 . Подставим
. Подставим 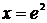 и
и 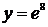 в общее решение, получим
в общее решение, получим 
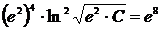 ,
,
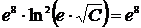 ,
,
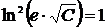 ,
,
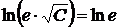 ,
,
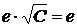 ,
,
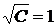 ,
,
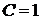 .
.
Тогда частное решение задачи Коши будет иметь вид 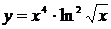 .
.
Дата добавления: 2018-04-05; просмотров: 309; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
