Метод непосредственного интегрирования
МИНОБРНАУКИ РОССИИ
Федеральное государственное бюджетное образовательное учреждение высшего образования
«Юго-Западный государственный университет»
(ЮЗГУ)
Кафедра высшей математики
УТВЕРЖДАЮ
Проректор по учебной работе
___________О.Г. Локтионова
«____»_____________2016 г.
НЕОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ.
ПРИЛОЖЕНИЯ ОПРЕДЕЛЁННОГО ИНТЕГРАЛА.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Методические указания по выполнению модуля 5,6,7
для студентов специальности «Таможенное дело»
Курск 2016
УДК 517
Составители: О.А. Бредихина, С.В. Шеставина
Рецензент
Кандидат технических наук, доцент кафедры высшей математики Н.А. Моргунова
Неопределённый интеграл. Приложения определённого интеграла. Дифференциальные уравнения: методические указания по выполнению модуля 5,6,7 для студентов специальности «Таможенное дело» / Юго-Зап. гос. ун-т; сост.: О.А. Бредихина, С.В. Шеставина. – Курск, 2016. – 56 с.: ил. 10, табл. 3, прилож. 0. – Библиогр.: с. 56.
Излагаются краткие методические рекомендации по темам математического анализа: неопределенные интегралы и методы их решения, определенный интеграл и его вычисления, приложения определенных интегралов, дифференциальные уравнения.
|
|
|
Текст печатается в авторской редакции
Подписано в печать ___________. Формат 60х84 1/16.
Усл. печ. л. . Уч.-изд. л. . Тираж экз. Заказ . Бесплатно.
Юго-западный государственный университет.
305040 Курск, ул. 50 лет Октября, 94.
Содержание
Введение………………………………………………………………..4
1. Неопределённый интеграл………………………………………….5
1.1 Основные понятия……………………………………………...5
1.2 Метод непосредственного интегрирования (задание 1)……..6
1.3 Метод замены переменной в неопределённом интеграле (задание 2)…………………………………………..…………...9
1.4 Метод интегрирования по частям (задание 3)………………13
1.5 Метод решения интегралов, содержащих квадратный трёхчлен в знаменателе (задание 4)...………………………...18
2. Определённый интеграл и его приложения……………………...20
2.1 Основные понятия…………………………………………….20
2.2 Вычисление площадей плоских фигур (задание 5)……..…..23
2.2.1 Вычисление площадей плоских фигур в декартовой
системе координат……………………………………………23
2.2.2 Вычисление площадей плоских фигур в
полярной системе координат………………………...………28
2.2.3 Вычисление площадей плоских фигур,
|
|
|
ограниченных линией, заданной параметрически…………..31
2.3 Вычисление длины дуги кривой (задание 6)……………..…34
3. Дифференциальные уравнения…………………………………...37
3.1 Дифференциальные уравнения первого порядка…………...38
3.1.1 Дифференциальные уравнения первого порядка с разделяющимися переменными (задание 7)…..…..................39
3.1.2 Линейные дифференциальные уравнения
первого порядка. Уравнения Бернулли (задание 8)…………42
3.2 Дифференциальные уравнения высших порядков………….46
3.2.1 Дифференциальные уравнения вида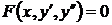 
(задание 9)……………………………………………………...46
3.2.2 Дифференциальные уравнения вида 
(задание 10)…………………………………………..………...50
3.2.3 Линейные однородные дифференциальные
уравнения второго порядка с постоянными
коэффициентами (задание 11)……………………………...…51
Список рекомендуемой литературы...................................................56
Введение
Цель настоящего методического пособия - научить студентов технике интегрирования и умению решать различные задачи на приложения определенных интегралов, а также помогает использовать свои знания в области интегрирования для решения дифференциальных уравнений.
Каждый параграф начинается с краткого теоретического введения, где приводится материал, содержащий основные понятия, формулы по данной теме. При подборе задач, авторы прежде всего исходили из учета тех трудностей, с которыми могут встретиться студенты на пути овладения методами интегрирования.
|
|
|
В работе приведены 50 примеров с подробными решениями по указанной тематике. При вычислении площадей плоских фигур, длины дуги кривой, решения иллюстрировались для наглядности рисунками и подробными пояснениями.
Данное пособие является приложением к модулю 5,6,7 для студентов специальности «Таможенное дело», в котором приведены индивидуальные задания по темам «Неопределенные интегралы», «Определенные интегралы и их приложения» и «Дифференциальные уравнения».
Авторы надеются, что это методическое издание поможет студентам в самостоятельной работе по выполнению модуля и изучению данного материала.
Неопределённый интеграл
Основные понятия
Функция 
называется первообразной для функции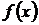 
на отрезке 
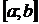, если она дифференцируема на этом отрезке и выполняется условие 
.
Неопределённым интегралом называется множество всех первообразных, то есть
,
где 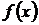– подынтегральная функция;
|
|
|
– подынтегральное выражение;
– дифференциал от переменной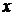 
.
Основные свойства неопределённого интеграла
1. Постоянный множитель выносится за знак интеграла, то есть 
, где 
.
2. Интеграл от суммы двух функций равен сумме интегралов от этих функций, то есть 
.
3. 
, где .
Основные используемые интегралы приведены в таблице.
Таблица 1
Таблица неопределённых интегралов
| № | Формула | № | Формула |
| 1 | 2 | 3 | 4 |
| 1 | 
| 12 | 
|
| 2 |  , где 
| 13 | 
|
| 2* | 
| 13* |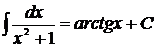 
|
| 3 | 
| 14 |
или
|
| 4 | 
|
Продолжение таблицы 1
| 1 | 2 | 3 | 4 |
| 4* | 
| 15 | 
|
| 5 | 
| 15* |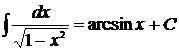 
|
| 6 |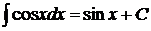 
| 16 | 
|
| 7 | 
| 17 | 
|
| 8 | 
| 18 | 
|
| 9 | 
| 19 | 
|
| 10 | 
| 20 |
|
| 11 | 
| ||
| 21 |
| ||
| 22 |
| ||
В данном модуле рассматриваются следующие методы интегрирования: метод непосредственного интегрирования, метод подведения под знак дифференциала, метод замены переменной, метод интегрирования по частям, метод решения интегралов вида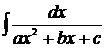 
и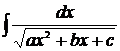 
. Рассмотрим каждый из них.
Метод непосредственного интегрирования
(задание 1)
Найти интеграл, используя свойства интегралов и табличное интегрирование, результат проверить дифференцированием.
При решении таких заданий используются основные свойства неопределённого интеграла и таблица 1. Иногда помогают метод группировки или почленное деление. Приведём ряд заданий, при решении которых используются данные методы.
Пример 1 
Решение
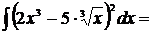[воспользуемся формулой квадрата разности]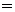 
[свойство неопределённого интеграла №2] 
[свойство неопределённого интеграла №1] 
[таблица 1, формула №2]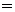
Проверка
Пример 2 
Решение
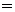[таблица 1, формула №15] 
.
Проверка
Теперь рассмотрим примеры, где при решении используется метод почленного деления.
Пример 3 
Решение
[таблица 1, формулы №1 и №3] 
.
Проверка
Пример 4 
Решение
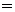[таблица 1, формулы №15 и №16] 
.
Проверка
Приведём ряд заданий, при решении которых используется метод группировки.
Пример 5 
Решение
[таблица 1, формулы №3 и №13*] 
.
Проверка
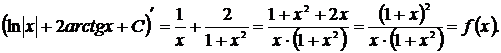
Пример 6 
Решение
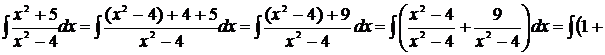
[таблица 1, формулы №1 и №14]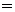
.
Проверка
Если интеграл не находится одним из выше перечисленных методов, то следующими методами являются метод внесения под знак дифференциала или метод замены переменной.
Дата добавления: 2018-04-05; просмотров: 400; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!