Вычисление длины дуги кривой (задание 6)
Вычислить длину дуги кривой, заданной явно, или параметрически, или в полярных координатах, используя определенный интеграл.
Пусть функция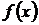 
непрерывно дифференцируема на 
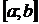, тогда длина дуги кривой 
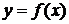на указанном промежутке вычисляется по формуле
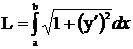. (1)
Если гладкая кривая задана в полярных координатах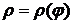 
и 
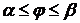, то длина ее дуги равна
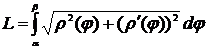. (2)
Если кривая гладкая и задана параметрически, то длина дуги этой кривой при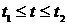 
вычисляется по формуле
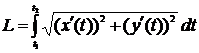. (3)
Пример 31
Вычислить длину дуги кривой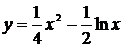 
от 
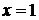до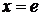 
.
Решение
Предварительно найдём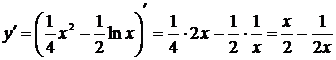 
.
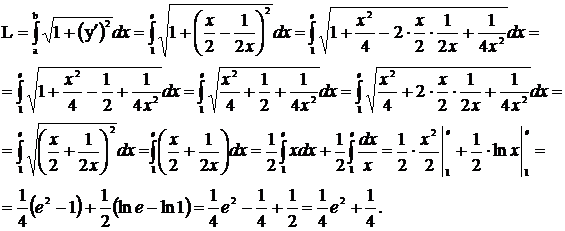
Пример 32
Вычислить длину дуги кривой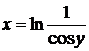 
от 
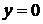до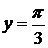 
.
Решение
Предварительно найдём
.
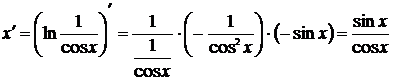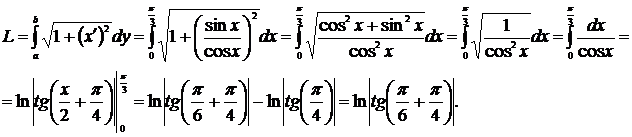Воспользовавшись формулой 
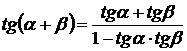, получаем окончательный ответ
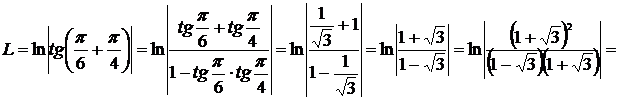
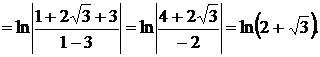
Пример 33
Вычислить длину дуги кривой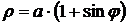 
от 
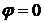до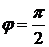 
.
Решение
Предварительно найдём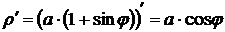 
.
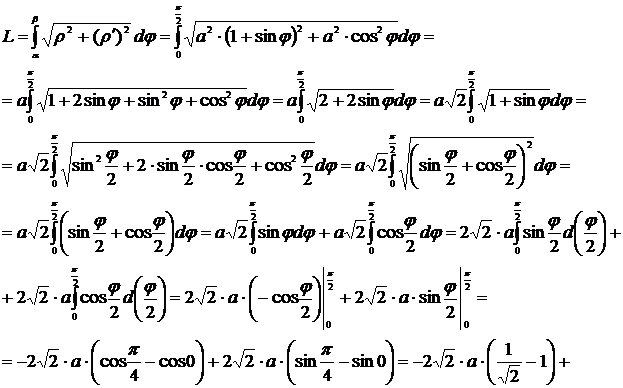
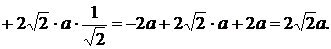
Пример 34
Вычислить длину кривой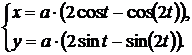 
Решение
Предварительно найдём
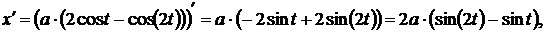
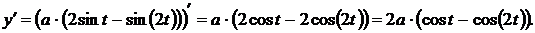
Пределы интегрирования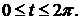 
Рис. 10
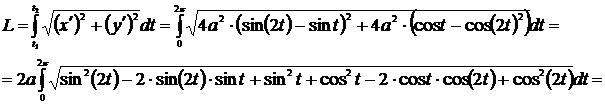
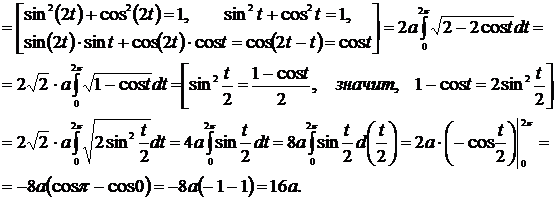
Дифференциальные уравнения
Всякое уравнение, содержащее по крайней мере одну производную неизвестной функции, называется дифференциальным уравнением.
В общем виде дифференциальное уравнение можно записать в ви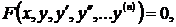де 
где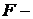 
некоторая функция от 
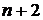переменных, 
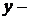некоторая функция от 
, 
.
|
|
|
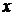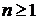Порядок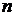 
старшей производной, входящей в запись уравнения, называется порядком дифференциального уравнения.
Если из уравнения в общем виде выразить в явном виде старшую производную, то получим уравнение вида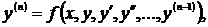 
называемое уравнением, разрешённым относительно старшей производной.
Функция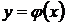 
называется решением дифференциального уравнения, если последнее обращается в тождество после подстановки .
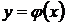Обычно дифференциальное уравнение имеет бесконечное множество решений. Для выделения из множества решений отдельного, называемого частным решением, необходимо задавать дополнительные условия в виде
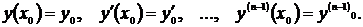
Задача нахождения решения, удовлетворяющего дополнительным условиям, называется задачей Коши, а решение уравнения – решением задачи Коши.
Дифференциальные уравнения первого порядка
Дифференциальное уравнение первого порядка имеет общий вид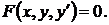 
Дифференциальное уравнение первого порядка, разрешённое относительно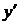 
, имеет вид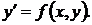 
Дифференциальное уравнение первого порядка, разрешённое относительно производной, можно также записать в дифференциальной форм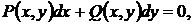е 
где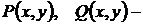 
известные функции.
Условие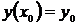 
называется начальным условием.
Общим решением дифференциального уравнения первого порядка называется функция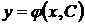 
, содержащая одну произвольную постоянную и удовлетворяющая условиям:
|
|
|
- функция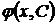 
является решением дифференциального уравнения при каждом фиксированным значении С;
- каково бы ни было начальное условие, можно найти такое значение постоянной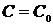 
, что функция 
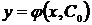, удовлетворяет заданному начальному условию.
Частным решением дифференциального уравнения первого порядка называется функция 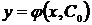, полученная из общего решения 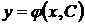при конкретном значении постоянной .
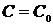Дата добавления: 2018-04-05; просмотров: 361; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!