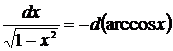Метод замены переменной в неопределённом интеграле (задание 2)
Найти интеграл, используя метод замены переменной, подведения функции под знак дифференциала, результат проверить дифференцированием.
Метод подведения под знак дифференциала основан на равенстве 
. То есть главной задачей является приведение подынтегрального выражения к виду 
. При этом нужно пользоваться формулой для расчёта дифференциала функции 
.
Наиболее часто встречающиеся дифференциалы приведены в таблице 2.
Таблица 2
Таблица основных дифференциалов
| № | Формула | № | Формула |
| 1 | 
| 7 | 
|
| 2 | 
| 8 | 
|
| 3 | 
| 9 |
или
|
| 4 | 
| ||
| 5 | 
| 10 |
или
|
| 6 | 
|
Пример 7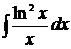 
Решение
[таблица 2, формула №3] 
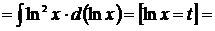
[таблица 1, формула №2] 
Проверка
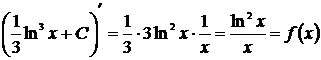
Пример 8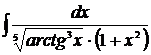 
Решение
[таблица 2, формула №9]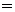 
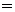[таблица 1, формула №2] 
Проверка
Пример 9 
Решение
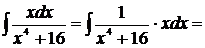[таблица 2, формула №1] 
[таблица 1, формула №13]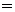
Проверка
Замечание: часто при нахождении неопределённых интегралов полезно пользоваться формулой
, где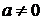 
.
Пример 10 
Решение
[таблица 1, формула №5] 
Проверка
Приём подведения под знак дифференциала есть частный случай замены переменной в неопределённом интеграле. Замена переменной под знаком интеграла может производиться в двух формах:
– в прямой, используя формулы 
, 
;
– в обратной, используя формулы 
, 
.
Наиболее часто применяется обратная форма замены переменной.
Пример 11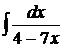 
Решение
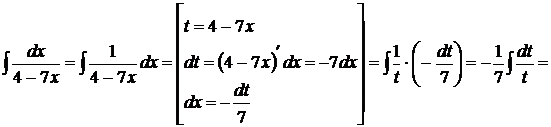
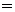[таблица, формула №3] 
Проверка
Прямую форму замены переменной чаще всего используют в случае, когда производная 
является производной достаточно сложной функции и гораздо проще найти производную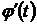 
.
Пример 12 
Решение
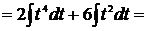[таблица 1, формула №2] 
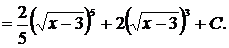
Проверка
Метод интегрирования по частям (задание 3)
Найти интеграл, используя формулу интегрирования по частям, результат проверить дифференцированием.
Пусть 
и 
– функции, имеющие непрерывные первые производные на рассматриваемом интервале. Тогда справедлива формула интегрирования по частям: 
.
Данный метод применяется, если
1.Подынтегральная функция – это тригонометрическая или показательная функция, умноженная на какой-нибудь многочлен, то есть представляет собой произведение вида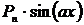 
, 
, 
, 
, где 
многочлен степени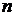 
. При этом, за 
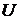берётся 
.
Пример 13 
Решение
Проверка
Иногда формулу интегрирования по частям следует использовать несколько раз.
Пример 14 
Решение
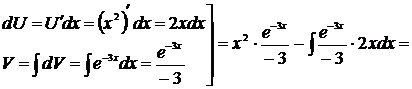
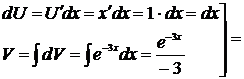
В процессе этого решения был найден следующий интеграл:
[таблица 1, формула №4*] 
Проверка
2.Подынтегральная функция – это обратная тригонометрическая функция, умноженная на какой-нибудь многочлен, то есть произведение вида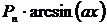 
, 
, 
, 
, либо логарифмическая функция, умноженная на какой-нибудь многочлен, то есть произведение вида 
, 
, 
, где многочлен степени .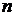
При этом, за 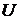берётся в первом случае обратная тригонометрическая, а во втором – логарифмическая функция.
Пример 15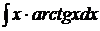 
Решение
[таблица 1, формулы №1 и №13*] 
Проверка
Замечание: случай, когда многочлен имеет нулевую степень не исключается.
Пример 16 
Решение
[таблица 1, формула №1] 
Проверка
3.Подынтегральная функция – это произведение показательной и тригонометрической функций, то есть произведение вида 
, 
, 
, 
. Здесь, дважды проинтегрировав по частям, приходим к линейному относительно исходного интеграла уравнению. Выразив из него интеграл, находим одну из первообразных.
При этом, 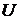можно принимать как показательную, так и тригонометрическую функцию, однако, интегрируя по частям второй раз, за 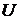нужно принимать соответственно первому разу показательную, либо тригонометрическую функцию.
Пример 17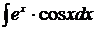 
Решение
.
После введения замены 
, получим уравнение, линейное относительно переменной 
. Решая его, находим значение одной из первообразных.
,
,
.
Таким образом, решение исходного интеграла примет вид
Проверка
Замечание: аналогичным способом можно решать интегралы с подынтегральной функцией вида 
, 
и т.п.
Пример 18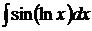 
Решение
.
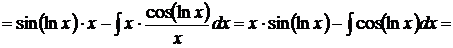
После введения замены 
, получим уравнение, линейное относительно переменной . Решая его, находим значение одной из первообразных.
,
,
.
Таким образом, решение исходного интеграла примет вид
Проверка
Дата добавления: 2018-04-05; просмотров: 635; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!