Метод решения интегралов, содержащих квадратный трёхчлен в знаменателе (задание 4)
Найти интеграл, содержащий квадратный трехчлен в знаменателе, результат проверить дифференцированием.
Для того, чтобы привести интеграл вида 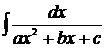 или
или 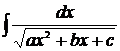 к табличному, следует выделить полный квадрат в квадратном трёхчлене знаменателя. При этом можно использовать формулу
к табличному, следует выделить полный квадрат в квадратном трёхчлене знаменателя. При этом можно использовать формулу
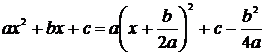 .
.
Затем выражение в скобках необходимо взять за новую переменную. Исходный интеграл при этом сводится к табличному (см. формулы №13-16 таблицы 1).
Пример 19 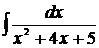
Решение
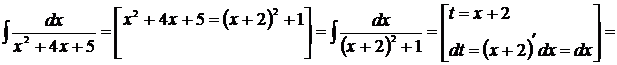
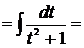 [таблица 1, формула №13*]
[таблица 1, формула №13*] 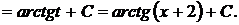
Проверка
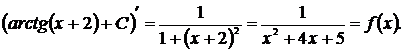
Пример 20 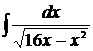
Решение
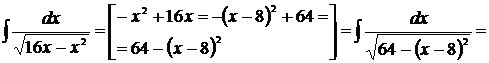
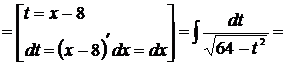 [таблица 1, формула №15]
[таблица 1, формула №15] 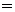
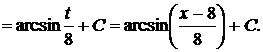
Проверка
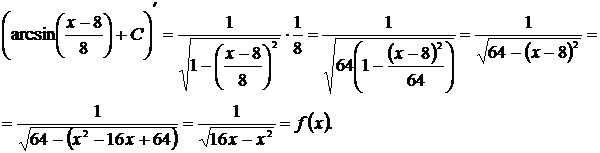
Пример 21 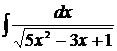
Решение
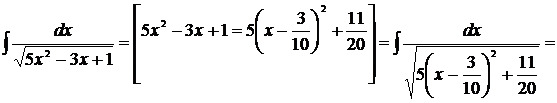
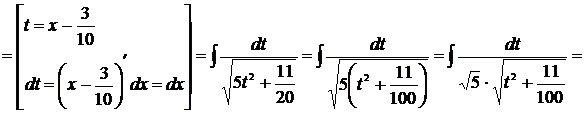
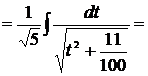 [таблица 1, формула №16]
[таблица 1, формула №16] 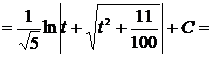
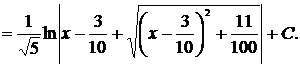
Проверка
Определённый интеграл и его приложения
Основные понятия
Пусть на отрезке 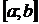 задана функция
задана функция 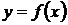 . Разобьём этот отрезок на
. Разобьём этот отрезок на 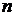 частей точками
частей точками 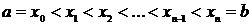 . На каждом малом отрезке
. На каждом малом отрезке 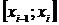 , где
, где 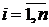 , выберём точку
, выберём точку 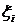 , найдём значение функции в этой точке
, найдём значение функции в этой точке 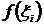 и составим сумму
и составим сумму 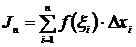 , где
, где 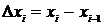 .
.
Сумма 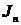 называется интегральной суммой для функции
называется интегральной суммой для функции 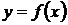 на
на 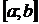 .
.
Определённым интегралом от функции 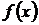 на отрезке
на отрезке 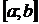 называется предел интегральной суммы
называется предел интегральной суммы 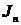 при условии, что длина наибольшего частичного отрезка
при условии, что длина наибольшего частичного отрезка 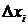 стремится к нулю
стремится к нулю  ,
,
где 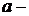 нижний предел интегрирования;
нижний предел интегрирования;
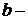 верхний предел интегрирования;
верхний предел интегрирования;
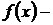 подынтегральная функция;
подынтегральная функция;
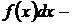 подынтегральное выражение.
подынтегральное выражение.
Замечание: определённый интеграл есть число.
Свойства определённого интеграла
Свойства определённого интеграла аналогичны свойствам неопределённого интеграла. Дополнительные свойства:
|
|
|
1. 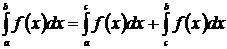 , где
, где 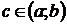 ;
;
2. 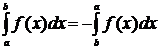 ;
;
3. 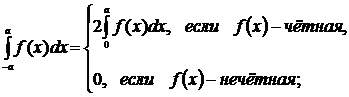
4. Пусть функция 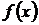 непрерывна на
непрерывна на 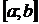 , тогда существует по крайней мере одна точка
, тогда существует по крайней мере одна точка 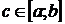 такая, что выполнено равенство
такая, что выполнено равенство 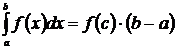 . Здесь
. Здесь 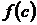 называется средним значением функции.
называется средним значением функции.
Способы вычисления определённого интеграла:
1. Теорема Ньютона-Лейбница.
Пусть 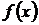 непрерывна на отрезке
непрерывна на отрезке 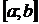 и
и 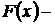 одна из её первообразных, тогда справедлива формула
одна из её первообразных, тогда справедлива формула
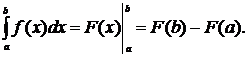
Пример 22 
Решение
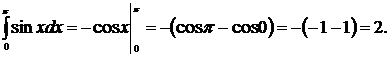
2.Замена переменной.
Необходимо вычислить интеграл 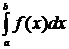 , где
, где 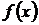 непрерывная функция на
непрерывная функция на 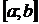 . Перейдем к новой переменной
. Перейдем к новой переменной 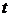 , полагая
, полагая 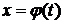 . Пусть
. Пусть 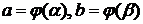 , кроме того, при изменении
, кроме того, при изменении 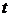 от
от 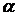 до
до 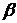 значения функции
значения функции 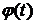 не выходят за пределы отрезка
не выходят за пределы отрезка 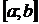 . Предположим, что функция
. Предположим, что функция 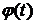 непрерывно дифференцируема на промежутке
непрерывно дифференцируема на промежутке 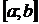 , то справедлива следующая формула замены переменной
, то справедлива следующая формула замены переменной 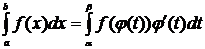 .
.
Пример 23 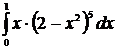
Решение
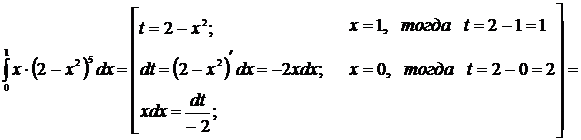
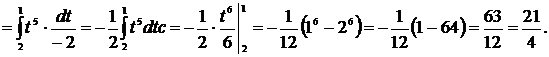
3. Формула интегрирования по частям.
Пусть 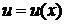 и
и 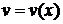 - непрерывные функции вместе со своими первыми производными на
- непрерывные функции вместе со своими первыми производными на 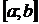 , тогда справедлива формула интегрирования по частям
, тогда справедлива формула интегрирования по частям 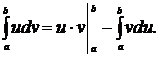
Пример 24 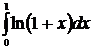
Решение
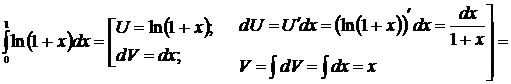
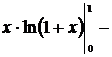
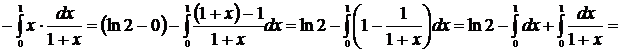
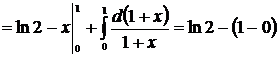
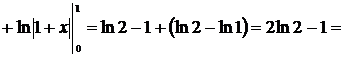
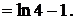
Вычисление площадей плоских фигур
(задание 5)
С помощью определенного интеграла вычислить площадь фигуры, ограниченной линиями.
Вычисление площадей плоских фигур в декартовой системе координат
|
|
|
Пусть на отрезке 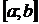 задана непрерывная функция
задана непрерывная функция 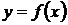 , причём
, причём 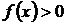 . Фигура, ограниченная сверху графиком
. Фигура, ограниченная сверху графиком 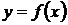 , снизу – осью Оx, сбоку прямыми
, снизу – осью Оx, сбоку прямыми 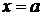 ,
, 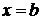 (рис. 1а), называется криволинейной трапецией.
(рис. 1а), называется криволинейной трапецией.
Геометрическим смыслом определённого интеграла являетсяплощадь криволинейной трапеции, вычисляемая по формуле
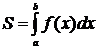 .
.
Если фигура, площадь которой необходимо вычислить, ограничена сверху графиком функции 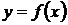 , снизу – графиком функции
, снизу – графиком функции 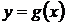 , а сбоку прямыми
, а сбоку прямыми 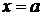 ,
, 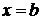 (рис 1.б), то её площадь вычисляется по формуле
(рис 1.б), то её площадь вычисляется по формуле
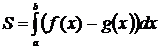 .
.
Частным случаем при этом является нахождение площади фигуры, ограниченной сверху осью Оx, снизу – графиком функции 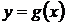 , а сбоку прямыми
, а сбоку прямыми 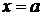 ,
, 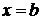 (рис 1.в). В этом случае, в предыдущую формулу следует подставлять
(рис 1.в). В этом случае, в предыдущую формулу следует подставлять 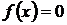 , тогда формула для вычисления площади такой фигуры имеет вид
, тогда формула для вычисления площади такой фигуры имеет вид
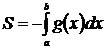 .
.
В некоторых случаях, чтобы вычислить площадь искомой фигуры, необходимо разбить ее на сумму или разность двух или более криволинейных трапеций (рис. 1г).
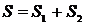 , где
, где 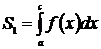 ,
, 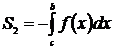 .
.
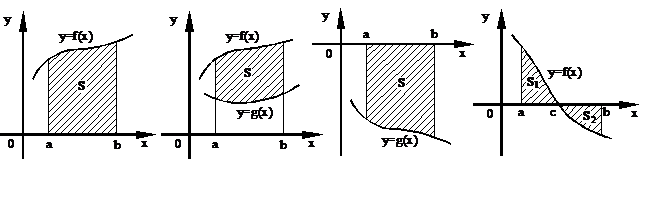
а) б) в) г)
Рис. 1
Пример 25
Вычислить площадь фигуры, ограниченной графиками функций 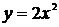 ,
, 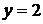 .
.
|
|
|
Решение
1. Вершиной параболы 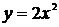 является точка
является точка 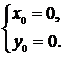
2. Точки пересечения параболы и прямой находятся из системы 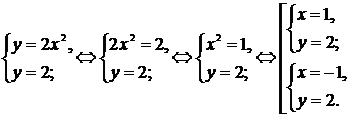
3. Используя найденные точки, строим графики заданных функций в декартовой системе координат.
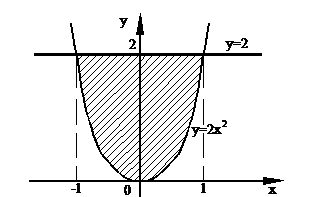 4. Сверху фигура ограничена прямой
4. Сверху фигура ограничена прямой 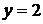 , значит
, значит 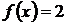 , снизу – параболой, значит
, снизу – параболой, значит 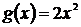 .
.
По графику видно, что 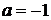 ,
, 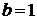 .
.
1способ: площадь полученной фигуры можно вычислить по формуле:
Рис. 2
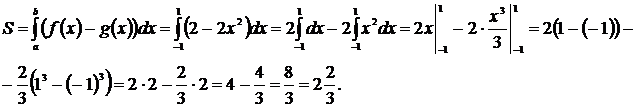 2 способ: полученная фигура симметрична, значит
2 способ: полученная фигура симметрична, значит
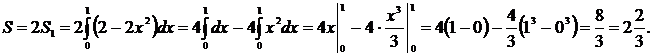
Пример 26
Вычислить площадь фигуры, ограниченной кривой 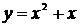 , прямыми
, прямыми 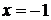 ,
, 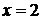 и осью Оx.
и осью Оx.
Решение
1. Вершиной параболы 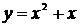 является точка
является точка 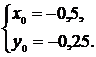
Замечание: координаты вершины параболы 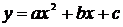 ,
, 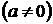 находятся по формулам
находятся по формулам 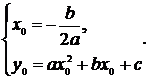
2. Точка пересечения параболы и прямой 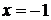 находится из системы
находится из системы 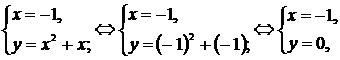
а с прямой 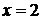 находится из системы
находится из системы 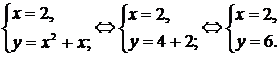
Точки пересечения параболы с осью Оx ( 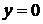 ) находятся из системы
) находятся из системы 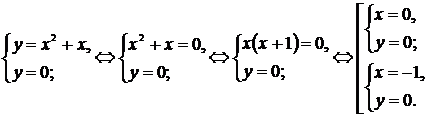
3. Используя найденные точки, строим графики заданных функций в декартовой системе координат.
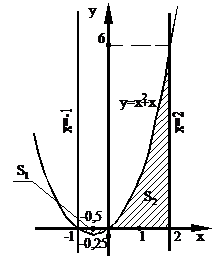 4. Площадь искомой фигуры
4. Площадь искомой фигуры  складывается из площадей
складывается из площадей  и
и  .
.
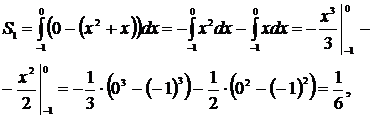
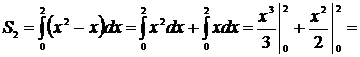
Рис. 3 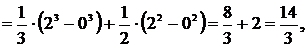
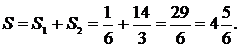
Если фигура, площадь которой необходимо вычислить, ограничена слева осью Oy, справа – графиком функции 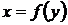 , а снизу и сверху прямыми
, а снизу и сверху прямыми 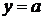 ,
, 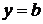 соответственно (рис. 4а), то её площадь вычисляется по формуле
соответственно (рис. 4а), то её площадь вычисляется по формуле
|
|
|
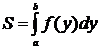 .
.
Если фигура, площадь которой необходимо вычислить, ограничена слева графиком функции 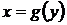 , справа – графиком функции
, справа – графиком функции 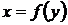 , а снизу и сверху прямыми
, а снизу и сверху прямыми 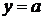 ,
, 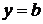 соответственно (рис. 4б), то её площадь вычисляется по формуле
соответственно (рис. 4б), то её площадь вычисляется по формуле
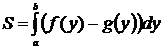 .
.
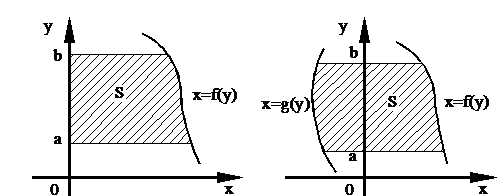
а) б)
Рис. 4
Пример 27
Вычислить площадь фигуры, ограниченной кривой 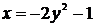 , прямой
, прямой 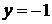 и осями координат.
и осями координат.
Решение
1. Вершиной параболы 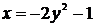 является точка
является точка 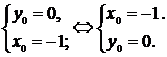
Замечание: координаты вершины параболы 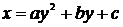 ,
, 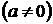 находятся по формулам
находятся по формулам 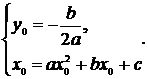
2. Точка пересечения параболы и прямой 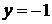 находится из системы
находится из системы 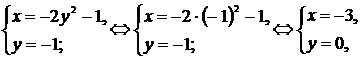
с осью Оx ( 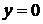 ):
): 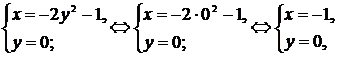
с осью Оy ( 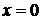 ):
): 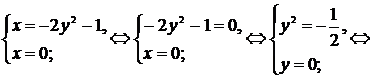 нет решения
нет решения
3. Используя найденные точки, строим графики заданных функций в декартовой системе координат.
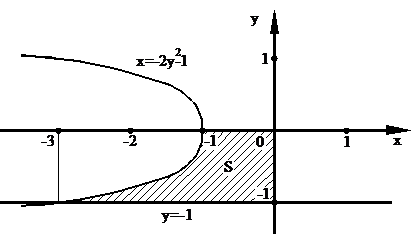
Рис. 5
4. Слева фигура ограничена параболой, справа – осью Oy, снизу – прямой 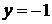 , сверху – осью Оx Таким образом, подставляя в формулу 6:
, сверху – осью Оx Таким образом, подставляя в формулу 6: 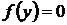 ,
, 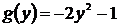 ,
, 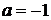 ,
,  , получим
, получим
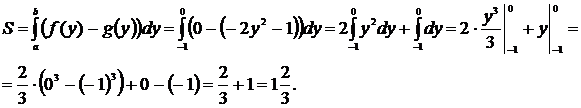
Дата добавления: 2018-04-05; просмотров: 541; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
