Некоторые распространенные весовые функции

⇐ ПредыдущаяСтр 4 из 9Следующая ⇒

Было предложено несколько вырезающих функций. Одной из наиболее широко используемых является весовая функция Хэмминга, которая определяется следующим образом:

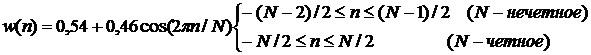
= 0 в других случаях.

Характеристики функции Хэмминга и прямоугольной функции сравниваются на рис. 3 во временной и частотной областях. Во временной области функция Хэмминга более мягко выходит на нуль с обеих сторон. В частотной области амплитуда ее главного лепестка шире (примерно вдвое), чем амплитуда прямоугольной функции, но ее боковые лепестки меньше по сравнению с главным (примерно на 40 дБ меньше главного лепестка по сравнению с 14 дБ для прямоугольной функции). Вследствие этого функция Хэмминга даст фильтр с большей полосой перехода (поскольку у нее шире главный лепесток), но и большим затуханием в полосе подавления (поскольку уровни боковых лепестков меньше).

Связь ширины полосы перехода (от полосы пропускания к полосе подавления) фильтра, построенного на основе функции Хэмминга, с длиной фильтра выражается следующей формулой:

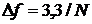
где N – длина фильтра, а – нормированная ширина полосы перехода. Максимальное затухание в полосе подавления, возможное при использовании функции Хэмминга, составляет порядка 53 дБ, а минимальная амплитуда неравномерности в полосе пропускания составляет около 0,0194 дБ.

Основные характеристики самых распространенных весовых функций собраны в табл. 3. Отметим, что первые четыре функции имеют фиксированные характеристики, такие как ширина перехода и затухание в полосе подавления. Следовательно, их использование ограничивает свободу разработчика. Отметим также, что фильтр, построенный с помощью метода взвешивания, имеет равные неравномерности в полосе пропускания и полосе подавления, т.е. 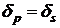. На практике это ограничение может дать фильтр, неравномерность которого в полосе пропускания будет излишне малой.

Таблица 3

Важные особенности распространенных весовых функций

Функция	Ширина перехода (нормированная), Гц	Неравномерность в полосе пропускания, дБ	Главный лепесток относительно бокового лепестка	Затухание в полосе подавления, дБ	Формула
Прямоугольная	0.9/N	0.7416	13	21	1
Хеннинга	3.1/N	0.0546	31	44
Хэмминга	3.3/N	0.0194	41	53
Блэкмена	5.5/N	0.0017	57	75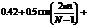
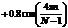
Кайзера	2.93/N(β=4.54) 4.32/N(β=6.76) 5.71/N(β=8.96)	0.0274 0.00275 0.000275		50 70 90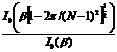

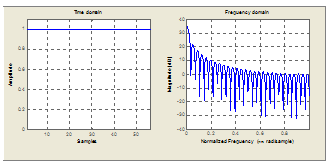
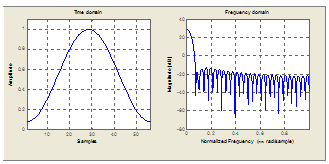
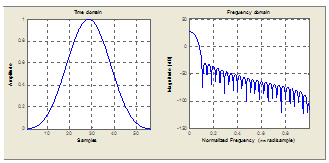
Рис. 3. Сравнение характеристик распространенных весовых функций во временной и частотной областях: а) прямоугольная функция; б) функция Хэмминга; в) функция Блэкмена

Окно Кайзера (Kaiser window function) несколько сглаживает очерченные выше проблемы, поскольку имеет параметр, управляющий неравномерностью, β, что позволяет разработчику играть на компромиссах между шириной перехода и неравномерностью. Функция Кайзера задается следующим образом:

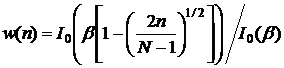
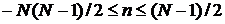
= 0 в других случаях

где 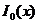— модифицированная функция Бесселя первого рода нулевого порядка. Управляющий параметр β отвечает за спад вырезающей функции на краях (во временной области). Для вычисления 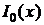обычно используется следующее разложение в степенной ряд :

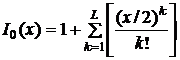
причем обычно L < 25. Эффективной реализацией указанного уравнения является алгоритм Кайзера.

При β = 0 функция Кайзера соответствует прямоугольной весовой функции, а при β = 5,44 функция весьма похожа на функцию Хэмминга (хотя и не идентична ей). Значение β определяется требованиями к затуханию в полосе подавления и его можно оценить с помощью одного из приведенных ниже эмпирических соотношений:

β = 0, если А < 21 дБ,

β = 0,5842(A – 21)^0,4 + 0,07886(А – 21), если 21 дБ < А < 50 дБ

β = 0,1102(A – 8,7), если А > 50 дБ,

где А = - 20lg(δ) – затухание в полосе подавления, δ = min(δ_p, δ_s), поскольку неравномерности в полосе пропускания и полосе подавления приблизительно равны, δ_p – желаемая неравномерность в полосе пропускания, a δ_s – желаемая неравномерность в полосе подавления. Число коэффициентов фильтра N подчиняется зависимости

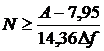
где 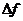– нормированная ширина полосы перехода. Далее полученные значения β и N используются для вычисления коэффициентов функции Кайзера w(n).

Метод взвешивания: резюме

1) Задать "идеальную" или желаемую частотную характеристику фильтра H_D(ω)

2) Получить импульсную характеристику h_D(n) желаемого фильтра, найдя
для этого Фурье–образ частотной характеристики. Выражения для
h_D(n) стандартных частотно-избирательных фильтров приведены в табл. 2.

3) Выбрать весовую функцию, которая удовлетворяет требованиям к полосе пропускания или затуханию , а затем определить число коэффициентов фильтра, использовав подходящее выражение для связи длины фильтра с шириной перехода, (записываются через частоту дискретизации).

4) Получить значения выбранной весовой функции w(n) и значения коэффициентов реального КИХ–фильтра h(n), умножив h_D(n) на w(n):

h(n) = h_D(n) w(n).

Очевидно, что метод вырезания – это прямолинейный метод, включающий минимум вычислений. В действительности при таком подходе коэффициенты можно вычислить с помощью карманного калькулятора. Впрочем, существуют и компьютерные программы вычисления h(n), но следует отметить, что фильтр, полученный описанным способом, не является оптимальным, т.е. во многих случаях иные методы позволяют получить аналогичный фильтр с меньшим числом коэффициентов.

Дата добавления: 2018-04-05; просмотров: 1019; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 345 6 7 8 9 Следующая ⇒

Мы поможем в написании ваших работ!