Обратные системы и их пределы
Пусть даны:
a) произвольное множество 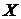 ,
,
b) упорядоченно (или квазиупорядоченное) отношение  множество
множество  ,
,
c) функция  , такая, что
, такая, что 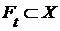 для каждого
для каждого  ,
,
d) функция  , которую можно записать в виде
, которую можно записать в виде 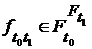 или
или 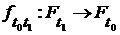 , где
, где  (1)
(1)
Пусть функция  удовлетворяет условиям
удовлетворяет условиям 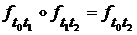 (2),
(2),
 для каждого
для каждого  является равенством (3)
является равенством (3)
Система  называется обратной системой. Обратным пределом этой системы, обозначенным
называется обратной системой. Обратным пределом этой системы, обозначенным  или
или  , называется подмножество произведения
, называется подмножество произведения 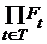 , состоящее из таких элементов
, состоящее из таких элементов  , что
, что
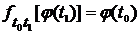 (4).
(4).
Пусть 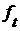 обозначает
обозначает  -ю координатную функцию
-ю координатную функцию  , т.е. функцию
, т.е. функцию  , определенную равенством
, определенную равенством
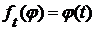 (5)
(5)
тогда
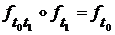 (6)
(6)
Если даны две обратные системы : 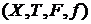 и
и  и функция
и функция  , т.е.
, т.е.  , и диаграмма
, и диаграмма

| ||||
 
| 
| |||

| 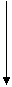  
| 
| 
| |

| 
| 
| ||
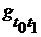
|
Коммутативна, т.е.  , если
, если  , то можно так определить отображение
, то можно так определить отображение  , чтобы диаграмма
, чтобы диаграмма
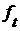
| ||||
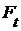
| 
| 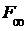
| ||

|   
| 
| 
| |

| 
| 
| ||

|
Была коммутативна для каждого  .
.
Для этого достаточно для каждого  задать
задать 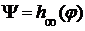 условием
условием  .
.
Легко доказать, что если  - взаимно однозначное отображение множества
- взаимно однозначное отображение множества 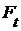 на
на  для каждого
для каждого  , то
, то  - взаимно однозначное отображение множества
- взаимно однозначное отображение множества 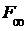 на
на  .
.
Пример 1. Пусть множество  упорядочено отношением равенства. Тогда
упорядочено отношением равенства. Тогда 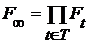 .
.
Пример 2. Пусть множество  направлено ( глава II, §5. Определение 2. Множество
направлено ( глава II, §5. Определение 2. Множество  , упорядоченное (или квазиупорядоченное) отношением
, упорядоченное (или квазиупорядоченное) отношением  , называется направленным, если, для каждой пары
, называется направленным, если, для каждой пары 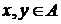 , существует такое
, существует такое  , что
, что  и
и  .),
.),  для каждого
для каждого  и
и  - тождественное отображение. Тогда
- тождественное отображение. Тогда 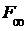 является множеством всех констант
является множеством всех констант  .
.
|
|
|
Для доказательства заметим, что если 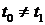 , то существует такое
, то существует такое 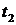 , что
, что 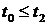 и
и  .
.
Отсюда  , и тогда, согласно (4),
, и тогда, согласно (4),  . Аналогично
. Аналогично  , поэтому
, поэтому  .
.
Пример 3. Множество  всех отображений
всех отображений 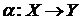 можно с помощью операции сужения
можно с помощью операции сужения  представить как обратный предел множества
представить как обратный предел множества  , где
, где  . Для этого надо в качестве направленного множества
. Для этого надо в качестве направленного множества  взять множество
взять множество 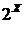 , упорядоченное отношением включения, функцию
, упорядоченное отношением включения, функцию  задать равенством
задать равенством 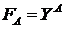 для
для  и каждой паре
и каждой паре  поставить в соответствие функцию
поставить в соответствие функцию  , определенную равенством
, определенную равенством 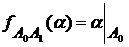 , где
, где 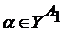 .
.
Здесь роль множества 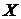 в обратной системе играет множество
в обратной системе играет множество 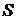 всех сужений, т.е.
всех сужений, т.е. 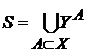 .
.
Поставим в соответствие каждому элементу  элемент
элемент  , определенный условием
, определенный условием 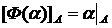 .
.
Легко проверить, что  , т.е.
, т.е.  .
.
При этом  отображает
отображает  на все множество
на все множество  . Действительно, пусть
. Действительно, пусть  , тогда
, тогда 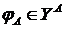 для каждого
для каждого 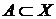 . Определим
. Определим  условием
условием  . Легко видеть, что
. Легко видеть, что 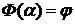 , т.е.
, т.е.  для
для 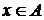 .
.
Наконец, отображение  взаимно однозначно. Действительно, если
взаимно однозначно. Действительно, если  , то существует такое
, то существует такое 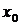 ,
, 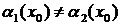 , т.е.
, т.е.  . Следовательно,
. Следовательно,  , так что
, так что  .
.
Следует отметить, что все эти рассуждения остаются в силе, если 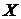 и
и  - метрические пространства. Тогда
- метрические пространства. Тогда 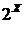 будет семейством компактных подмножеств пространства
будет семейством компактных подмножеств пространства 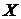 , а
, а  - семейством непрерывных отображений
- семейством непрерывных отображений 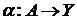 .
.
|
|
|
Бесконечные операции в решетках и булевых кольцах.
Утверждения, доказанные в предыдущих параграфах этой главы, можно рассматривать как термины о решетке 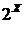 . Как мы знаем, эта решетка полна и является булевой алгеброй. Естественно возникает вопрос, можно ли обобщить термин №1 на произвольные решетки, полные решетки, булевы кольца.
. Как мы знаем, эта решетка полна и является булевой алгеброй. Естественно возникает вопрос, можно ли обобщить термин №1 на произвольные решетки, полные решетки, булевы кольца.
Предположим сначала, что  - произвольное упорядоченное множество и
- произвольное упорядоченное множество и  . Тогда справедливы теоремы, аналогичные теоремам 1-3 §1.
. Тогда справедливы теоремы, аналогичные теоремам 1-3 §1.
Теорема 1. Наименьшая верхняя грань  (наименьшая нижняя грань
(наименьшая нижняя грань  ), если она существует, является единственным элементом множества
), если она существует, является единственным элементом множества  , удовлетворяющим условиям:
, удовлетворяющим условиям:

(соответственно 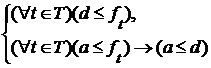 ).
).
Теорема 2. Если  и для каждого
и для каждого 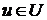 существует наименьшая верхняя грань
существует наименьшая верхняя грань  , и если существует наименьшая верхняя грань
, и если существует наименьшая верхняя грань  , то существует наименьшая верхняя грань
, то существует наименьшая верхняя грань 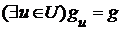 . Аналогично для наибольших нижних граней.
. Аналогично для наибольших нижних граней.
Теорема 3. Если  - перестановка множества
- перестановка множества  и существует наименьшая верхняя грань
и существует наименьшая верхняя грань  , то существует также наименьшая верхняя грань
, то существует также наименьшая верхняя грань  . Аналогично для наибольших нижних граней.
. Аналогично для наибольших нижних граней.
|
|
|
Для произвольного упорядоченного множества можно доказать утверждение, аналогичное (3), § 1.
Теорема 4. Если существуют грани  и
и  , то
, то 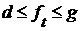 для всех
для всех  .
.
Формулы (4)-(11) § 1 не имеют аналогов в произвольных упорядоченных множествах.
Теорема 5. Если  - решетка,
- решетка,  и существуют наименьшие верхние грани
и существуют наименьшие верхние грани 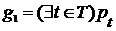 ,
,  , то существует наименьшая верхняя грань
, то существует наименьшая верхняя грань  и она равна
и она равна 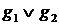 . Аналогично для наибольших нижних граней.
. Аналогично для наибольших нижних граней.
Д о к а з а т е л ь с т в о. В самом деле,  для любого
для любого  . Если
. Если 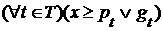 , то
, то  . Поэтому
. Поэтому  и аналогично
и аналогично  , откуда
, откуда 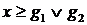 .
.
Условие, что  - решетка, мы использовали в самой формулировке теоремы. Для произвольного упорядоченного множества мы не смогли бы говорить о
- решетка, мы использовали в самой формулировке теоремы. Для произвольного упорядоченного множества мы не смогли бы говорить о  и
и 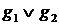 .
.
Теорема 6. Если  - решетка и существуют наименьшие верхние грани
- решетка и существуют наименьшие верхние грани 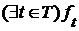 и
и  , то
, то  .
.
Дата добавления: 2018-04-04; просмотров: 229; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
