Теорема 3. Семейство содержит в качестве подмножеств каждое из семейств


Вообще говоря, никакие два из этих семейств не совпадают; кроме того, они не исчерпывают всего семейства  .
.
Опишем теперь метод, позволяющий решить, принадлежит ли данное множество, определенное при помощи высказывательной функции, семейству  .
.
Пусть  - высказывательная функция, переменные
- высказывательная функция, переменные  пробегают множество
пробегают множество 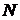 . Положим
. Положим  ,
,  , где каждый из символов
, где каждый из символов  обозначает либо квантор всеобщности, либо квантор существования.
обозначает либо квантор всеобщности, либо квантор существования.
Теорема 4. Если для произвольных  множество
множество  принадлежит
принадлежит  , то
, то  .
.
Д о к а з а т е л ь с т в о. Проведем индукцию по числу кванторов.
1) Если  , то
, то  и тогда
и тогда  по условию.
по условию.
2) Если теорема верна для  квантора, то каждое из множеств
квантора, то каждое из множеств  принадлежит
принадлежит  . Если
. Если  - квантор существования, то
- квантор существования, то  , а если
, а если  - квантор всеобщности, то
- квантор всеобщности, то  . В обоих случаях
. В обоих случаях  и теорема доказана.
и теорема доказана.
Наиболее интересный пример семейства  получим если в качестве
получим если в качестве  возьмём семейство
возьмём семейство  замкнутых множеств произвольного топологического пространства
замкнутых множеств произвольного топологического пространства 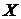 . В этому случае
. В этому случае  называется семейством борелевских множеств пространства
называется семейством борелевских множеств пространства 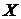 .
.
Пример. Докажем, что множество предельных точек последовательности непрерывных функций есть множество типа 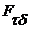 .
.
Для этого запишем условие Коши сходимости последовательности вещественных чисел  ,
,  , …,
, …,  ,…:
,…:
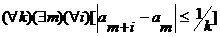
Отсюда видно, что множество  предельных точек последовательности непрерывных функций
предельных точек последовательности непрерывных функций 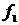 ,
, 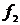 , ..., fn, …, имеет вид:
, ..., fn, …, имеет вид:
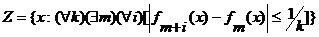
Полагая
 ,
,
получаем
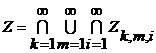 .
.
Т.к. 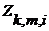 (при фиксированных индексах) замкнуто (это следует из непрерывности рассматриваемых функций), то
(при фиксированных индексах) замкнуто (это следует из непрерывности рассматриваемых функций), то  есть множество типа
есть множество типа 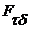 .
.
|
|
|
Обобщённые декартовы произведения.
Пусть  (как в §1) – функция, значениями которой являются подмножества множества
(как в §1) – функция, значениями которой являются подмножества множества 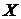 , а областью определения – множество
, а областью определения – множество  .
.
О п р е д е л е н и е. Декартовым произведением  называется множество таких функций
называется множество таких функций  с областью определения
с областью определения  , что
, что  для каждого
для каждого  :
:
 , где
, где  .
.
Если  , то вместо
, то вместо  пишут
пишут  . Элементами этого декартова произведения будут такие последовательности
. Элементами этого декартова произведения будут такие последовательности  , что
, что  для
для  .
.
Если все сомножители  равны,
равны, 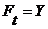 , то
, то  . Здесь
. Здесь  - множество функций с областью определения
- множество функций с областью определения  и множеством значений
и множеством значений  . Множество
. Множество  называется декартовой степенью множества
называется декартовой степенью множества  .
.
Для  обозначим через
обозначим через  проекцию множества
проекцию множества  на
на  , т.е.
, т.е.  . Очевидно, что
. Очевидно, что  для каждого
для каждого  .
.
Замечание. Пусть  . Декартовы произведения
. Декартовы произведения  и
и  не совпадают. Первое имеет в качестве элементов последовательности длины 2, второе – упорядоченные пары, а это различные понятия. Однако в действительности различие между этими двумя произведениями не существенно, потому что каждой упорядоченной паре
не совпадают. Первое имеет в качестве элементов последовательности длины 2, второе – упорядоченные пары, а это различные понятия. Однако в действительности различие между этими двумя произведениями не существенно, потому что каждой упорядоченной паре  можно поставить во взаимно однозначное соответствие последовательность
можно поставить во взаимно однозначное соответствие последовательность  . Если
. Если  для некоторого
для некоторого  , то
, то  .
.
В самом деле, если  , то
, то  , т.е.
, т.е.  .
.
|
|
|
Теорема 1. Если  - конечное множество и
- конечное множество и  для каждого
для каждого  , то
, то  .
.
Д о к а з а т е л ь с т в о. Проведем индукцию по числу элементов множества  . Если
. Если  имеет один элемент, то теорема очевидна. Предположим, что теорема взята в случае, когда
имеет один элемент, то теорема очевидна. Предположим, что теорема взята в случае, когда  имеет
имеет  элементов. Пусть
элементов. Пусть 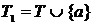 , где
, где 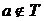 .
.
Пусть  для
для  . Докажем, что
. Докажем, что  . Возьмём
. Возьмём  и
и  . Тогда множество
. Тогда множество  будет функцией, принадлежащей
будет функцией, принадлежащей  , следовательно, множество
, следовательно, множество  непусто.
непусто.
Теорема 1 распространяется также на случай произвольного  , если все сомножители
, если все сомножители  совпадают.
совпадают.
Теорема 2. Если  , то
, то  .
.
В общем случае доказательство того, что декартово произведение непустых множеств непусто, требует аксиомы выбора.
ºTеорема 3. Если  для
для  , то
, то  .
.
Д о к а з а т е л ь с т в о. Элементами множества  будет функция выбора для семейства
будет функция выбора для семейства  .
.
Пользуясь декартовыми произведениями (например в алгебре, топологии и т.п.), мы обычно сталкиваемся со случаями, когда на множествах  определены некоторые операции или отношения или когда множества
определены некоторые операции или отношения или когда множества  являются топологическими пространствами. Рассмотрим сначала случай, когда на каждом множестве
являются топологическими пространствами. Рассмотрим сначала случай, когда на каждом множестве  определена только одна операция – для удобства будет считать её бинарной.
определена только одна операция – для удобства будет считать её бинарной.
Другими словами, кроме функции  , задана
, задана  такая функция
такая функция  двух переменных, что
двух переменных, что  для каждого
для каждого  .
.
|
|
|
Функция  определяет бинарную операцию
определяет бинарную операцию  на элементах декартова произведения
на элементах декартова произведения  :
:
 , где
, где  .
.
Таким образом,  - такой элемент
- такой элемент 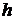 декартова произведения, что
декартова произведения, что 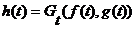 для всех
для всех  . Операция
. Операция  называется декартовым произведением операций
называется декартовым произведением операций  .
.
Аналогично определяется декартово произведение отношений. Пусть  - такая функция, что
- такая функция, что  (для каждого
(для каждого  ) есть отношение над полем, содержащимся в
) есть отношение над полем, содержащимся в  .
.
Декартовым произведением отношения называется такое отношение  над полем, содержащемся в
над полем, содержащемся в  , что
, что  .
.
Здесь надо заметить, что  - двуместное отношение, т.е. множество упорядоченных пар, в то время как
- двуместное отношение, т.е. множество упорядоченных пар, в то время как  - множество функций. Однако можно естественным образом поставить в соответствие декартову произведению
- множество функций. Однако можно естественным образом поставить в соответствие декартову произведению  отношение между функциями
отношение между функциями  , которое выполняется тогда и только тогда, когда функция
, которое выполняется тогда и только тогда, когда функция 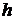 , определенная равенством
, определенная равенством  (т.е. функция
(т.е. функция  ), принадлежит
), принадлежит  . Это отношение совпадает с отношением
. Это отношение совпадает с отношением  .
.
Очевидно, что все эти определения без труда переносятся на случай, когда на каждом множестве  задача не одна, а произвольное число операций (или отношений).
задача не одна, а произвольное число операций (или отношений).
Пример. Предположим, что  - булево кольцо относительно операций
- булево кольцо относительно операций 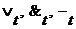 и элементов
и элементов  . Обозначим через
. Обозначим через  декартовы произведения операций
декартовы произведения операций 
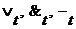 , а через
, а через 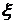 и
и  такие функции, что
такие функции, что  и
и  для всех
для всех  .
.
|
|
|
Теорема 4. Декартово произведение  является булевым кольцом относительно операций
является булевым кольцом относительно операций  и элементов
и элементов 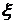 и
и  .
.
Д о к а з а т е л ь с т в о. Достаточно проверить справедливость аксиомы булевой алгебры (I – V', §9, гл. I). Проверим, например, справедливость (IV). Пусть  . По определению
. По определению  - это такая функция
- это такая функция 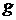 , что
, что  для каждого
для каждого  . Т.к. для
. Т.к. для  аксиома (IV) верна, то
аксиома (IV) верна, то  и, значит,
и, значит,  .
.
Булево кольцо  называется декартовым (или прямым) произведением булевых колец
называется декартовым (или прямым) произведением булевых колец  .
.
Аналогично определяется прямое произведение группы колец и других алгебраических систем.
Дата добавления: 2018-04-04; просмотров: 332; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
