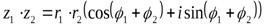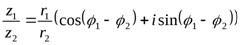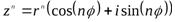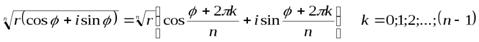Определение множества комплексных чисел
Когда-то давно, много тысяч лет назад, люди придумали натуральные числа. Это случилось тогда, когда возникла необходимость пересчитать множество людей в племени, множество животных, убитых на охоте, … Довольно скоро люди поняли, что одними натуральными им не обойтись и были придуманы дробные числа. Так, с течением времени, решая различные жизненные задачи, люди придумывали все новые числовые множества. Причем каждое следующее включало в себя предыдущее:
N– множество натуральных чисел: числа, используемые при счете предметов. (не всегда можно решить уравнение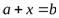 
).
Z– множество целых чисел:N + 0 + числа, противоположные натуральным. (не всегда можно решить уравнение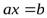 
).
Q– множество рациональных дробей (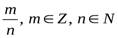 
– обыкновенные дроби, конечные десятичные дроби, бесконечные периодические десятичные дроби).
I– множество иррациональных чисел (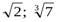 
, … бесконечные непериодические десятичные дроби).
R– множество действительных чисел, включает в себя все предыдущие множества.
В R не всегда можно решить уравнение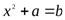 
. Значит, нужно новое множество, в котором всякое уравнение указанного типа было бы разрешимо. Таким числовым множеством является множествоC – комплексных чисел.
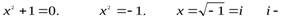мнимая единица – число, квадрат которого равен 
: 
.
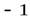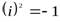Множеством C-комплексных чисел называется множество символов вида: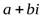 
, гдеаиb– любые действительные числа, 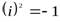и в котором выполняются следующие аксиомы:
|
|
|
А1: 
А2: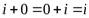 
А3: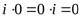 
А4: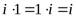 
А5: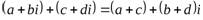 
А6: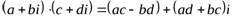 
Символы вида 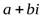называются комплексными числами
Любое действительное число можно представить в виде комплексного числа. Например,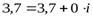 
, следовательно, множество действительных чисел является подмножеством множества комплексных чисел: 
.
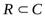Запись комплексного числа в виде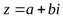 
называетсяалгебраическойформой комплексного числа.а– действительная часть комплексного числа (обозначается 
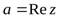);b– мнимая часть комплексного числа (обозначается ( 
)).
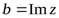Обозначение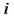 
для мнимой единицы ввел Л.Эйлер в 1777 г.
Операции над комплексными числами в алгебраической форме
Два комплексных числа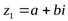 
и 
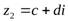называютсяравнымитогда и только тогда, когда равны их действительные и мнимые части, то есть: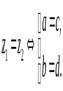 
Операции с комплексными числами в алгебраической форме выполняются по следующим правилам, аналогичным соответствующим правилам для многочленов (для любых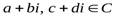 
):
- Сложение:
.
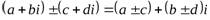Пример 1.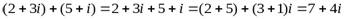 
;
.
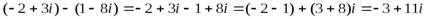- Умножение:
.
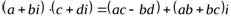Пример 2.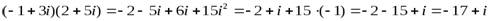 
.
Пусть дано комплексное число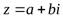 
.Сопряженнымдля него называется комплексное число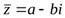 
Пример 3.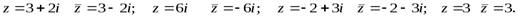 
Сумма и произведение двух комплексных сопряженных чисел есть действительное число:
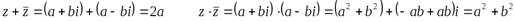
- Чтобы разделить одно комплексное число на другое в алгебраической форме нужно умножить числитель и знаменатель дроби на число, сопряженное знаменателю.
.
|
|
|
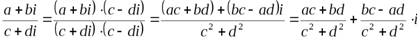Замечание:эти операции можно выполнять как действия с двучленами.
Пример 4.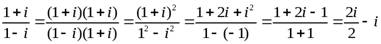 
;
.
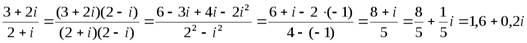Арифметические действия над комплексными числами подчиняются тем же законам, что и действия над действительными числами.
Есл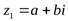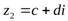и 
, 
и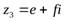 
– любые комплексные числа, то верны следующие равенства:
1) 
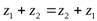– коммутативный закон для сложения;
2) 
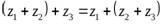– ассоциативный закон для сложения;
3) 
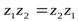– коммутативный закон для умножения;
4) 
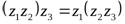– ассоциативный закон для умножения;
5) 
– дистрибутивный закон;
Число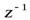 
, обратное данному числу 
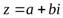, можно найти по формуле:
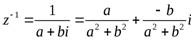
Натуральные степени мнимой единицы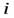 
принимают лишь четыре значения: , 
, 
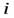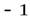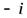и 1, определяемые формулами: 
, 
, 
, 
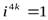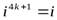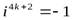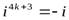, где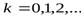 
При возведении комплексного числа 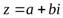в натуральную степень 
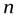пользуются формулой бинома Ньютона: 
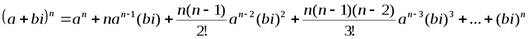. В правой части этого равенства заменяют степени мнимой единицы по соответствующим формулам и приводят подобные члены, в результате получают некоторое комплексное число 
.
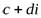Пример 5. Возвести в указанные степени данные комплексные числа: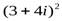 
, 
, 
.
.
.
.
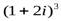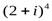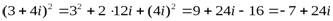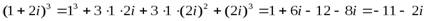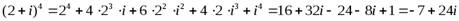Квадратным корнем из комплексного числа называют комплексное число, квадрат которого равен данному комплексному числу: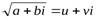 
, если 
.
|
|
|
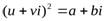Числа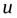 
и 
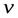определяются из равенств: 
, 
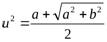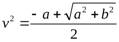, причем 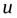и 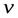будут действительными, так как при любых 
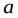и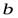 
выражения 
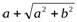и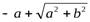 
являются положительными. Знак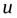и и 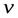выбирают так, чтобы выполнялось равенство 
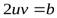. Извлечение квадратного корня из комплексного числа всегда возможно и лает два значения, различающиеся лишь знаком.
Пример 6.Извлечь квадратный корень из числа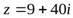 
.
Обозначим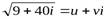 
. Так как в этом случае 
, 
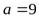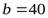, то получим:
, 
.
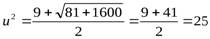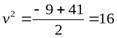Так как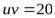 
, то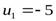 
, 
, 
, 
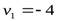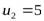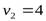. Получаем два значения корня: 
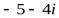и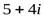 
.
2.3 Геометрическая интерпретация комплексных чисел
Пусть дано комплексное число .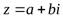
Любое комплексное число 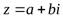вполне определяется упорядоченной парой действительных чисел 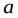и .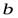
Упорядоченная пара действительных чисел задает на плоскости в прямоугольной системе координат вполне определенную точку с координатами аиb, гдеa– абсцисса,b– ордината точки. Поэтому можно сказать, что геометрически комплексное число есть некоторая точка на плоскости.
Положение любой точки на плоскости определяется заданием ее радиус-вектора, т.е. вектора, идущего из начала координат в данную точку.
Поэтому можно сказать, что любому комплексному числу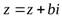 
на плоскости соответствует вполне определенный радиус-вектор.
Пример 7.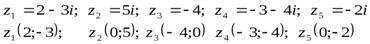 
2.4 Тригонометрическая форма комплексных чисел
|
|
|
П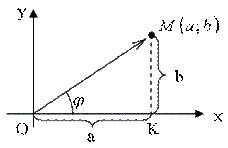 
усть дано комплексное число 
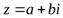. Положение точки 
на плоскости вполне определяется не только заданием ее декартовых координатaиb, но и заданием ее полярных координатrи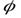 
, гдеr– длина радиус-вектора этой тачки, а 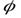– угол между положительным направлением оси 
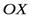и радиус вектором этой точки.
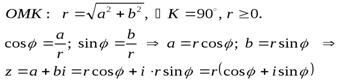
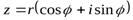–тригонометрическая форма комплексного числа.
r– модуль комплексного числа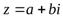 
.
Модулемкомплексного числаzназывают длину радиус-вектора точки, изображающей комплексное число или расстояние от начала координат до точки, изображающей комплексное число.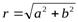 
.
–аргумент комплексного числа .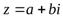
Аргументомкомплексного числа называют множество величин углов, образованных положительным направлением 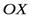и радиус-вектором точки, изображающейz. 
.
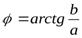Главным значением аргумента называют значение, принадлежащее промежутку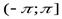 
(но можно использовать и промежуток 
).
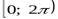При отыскании аргумента комплексного числа zнужно учитывать, в какой четверти находится точка, соответствующая данному комплексному числу.
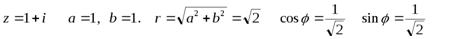
–угол первой четверти, т.к.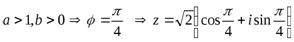 
2. 5 Действия над комплексными числами в тригонометрической форме
Пусть заданы два комплексных числа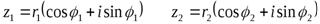 
Пример 8.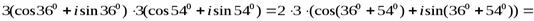 
.
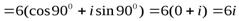Пример 9.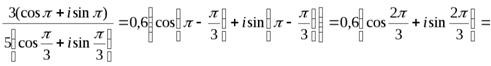 
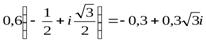
Пример 10.Найти шестую степень числа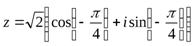 
.
.
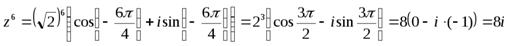Пример 11. Найти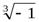 
.
Решение.
Представим число –1 в тригонометрической форме: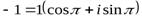 
.
, 
.
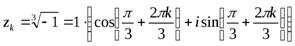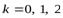Получаем последовательно три значения:
: 
;
: 
;
: 
.
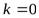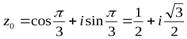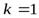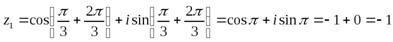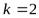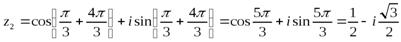Ответ.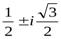 
, 
.
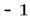Формула Эйлера устанавливает взаимосвязь между экспоненциальной функцией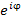 
и тригонометрическими функциям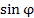и 
и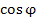 
на множестве комплексных чисел:
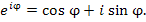(1)
где e — 1-на из самых важных математических констант, которая определяется при помощи формулы:
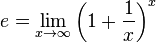
i — мнимая единица.
Другими словами формула Эйлера заявляет, что для всякого действительного числа и комплексного числа x выполняется равенство, указанное выше.
Дадим понятие функции от комплексного переменного.
Пусть даны две плоскости комплексных чисел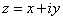 
и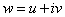 
(рис. 129). Рассмотрим некоторое множество
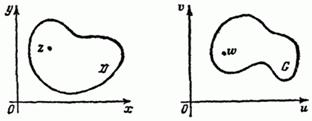
Рис. 129
точек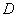 
в плоскости 
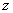и множество 
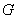в плоскости 
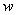. Если каждому числу 
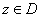по некоторому закону поставлено в соответствие определенное комплексное число 
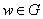, то говорят, что на множестве 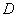задана однозначная функция комплексного переменного, отображающая множество 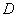в множество 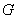. Символически это обозначают так:
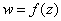
Множество 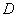называют областью определения функции 
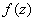. Если каждая точка множества 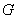является значением функции, то говорят, что 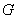- область значений этой функции или образ множества 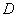при помощи функции 
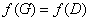. В этом случае говорят еще, что функция 
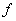отображает 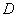на .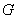
Функцию 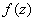можно записать в виде
,
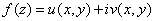
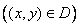где
,
,
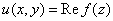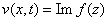
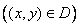- действительные функции от переменных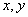 
.
Если каждому 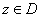соответствует несколько разных значений 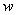, то функция 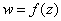называется многозначной.
Понятия предела и непрерывности функции комплексного переменного вводятся аналогично, как это делается для функции действительного переменного, необходимо лишь всюду вместо абсолютной величины писать модуль комплексного числа.
Говорят, что функция
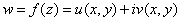
имеет предел в точке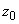 
, равный числу 
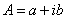, если
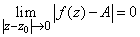. (1)
В этом случае пишут
.
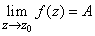На языке функци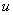й 
и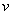 
свойство (1) записывается в виде равенства
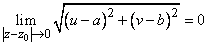(2)
или, что все равно, в виде двух равенств
, 
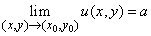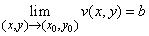. (3)
Для комплексных функци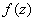й и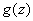 
имеют место свойства, аналогичные соответствующим свойствам действительных функций:
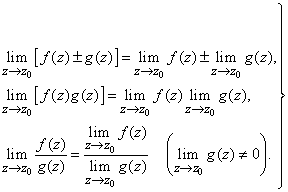(4)
Как обычно, формулы (4) надо понимать в том смысле, что если пределы, стоящие в их правых частях, существуют, то существуют также пределы, стоящие в их левых частях, и выполняется соответствующее равенство.
Функция 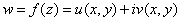называется непрерывной в точке 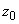, если для нее выполняется свойство
, 
, 
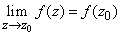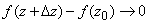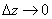. (5)
Таким образом, непрерывная в точке 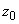функция должна быть определена в окрестности этой точки, в том числе и в ней самой и должно выполняться равенство (5). Равенство (5) эквивалентно двум равенствам:
, 
.
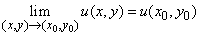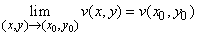Следовательно, непрерывность 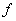в точке 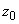эквивалентна непрерывности функци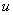й и 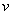в точке 
.
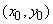Из свойств (4) следует, что сумма, разность, произведение и частное непрерывных в точке 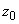комплексных функци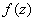й и 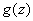есть непрерывная функция в этой точке. В случае частного надо в этой формулировке считать, что 
.
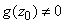Пример 1. Функция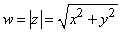 
задана на всей комплексной плоскости. Ее значения – неотрицательные числа. Эта функция непрерывна во всех точках комплексной плоскости:
.
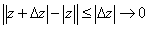
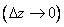Пример 2.
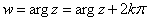
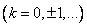. (6)
Эта функция многозначная (бесконечнозначная);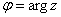 
- главное значение аргумента 
.
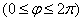Пример 3. Функция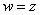 
. Она непрерывна:
.
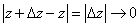
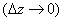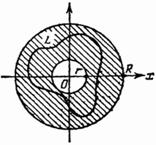
Рис. 130
Но тогда и функция 
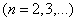непрерывна как произведение конечного числа непрерывных функций.
Множество комплексных чисел 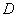будем называть областью, если 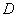, как множество точек плоскости, открыто и связно.
Область 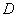называется односвязной, если любая непрерывная замкнутая самонепересекающаяся кривая, проведенная в 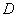, ограничивает некоторую область 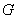, целиком принадлежащую 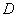. Область, не обладающую этим свойством, будем называть многосвязной.
Пример 4. Кольцо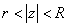 
- многосвязная (двусвязная) область. Кривая 
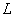(рис. 130) принадлежит кольцу, но ограничивает область, не входящую целиком в него.
ПРАКТИЧЕСКАЯ ЧАСТЬ
Типовые задачи
1.Операции с векторами на плоскости.
Представлены векторы
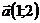и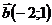
.
Определить:
1.1.Длины этих векторов.
1.2.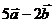 
.
1.3.Скалярное произведение данных векторов и угол между ними.
РЕШЕНИЕ:
2.Операциисвекторамивпространстве.
Представлены векторы
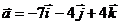и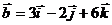 
.
Определить:
1.4.Длины этих векторов.
1.5.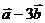 
.
1.6.Скалярное произведение данных векторов и угол между ними.
3.Векторное и смешанное произведение векторов.
1.7.Определить объём параллелепипеда, построенного на векторах
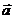(1;0;1), 
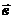(4;-1;-1), 
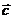(1;0;1).
РЕШЕНИЕ:
4.Прямые и окружности на плоскости.
1.8.Составить уравнение прямой, представленной на рисунке.
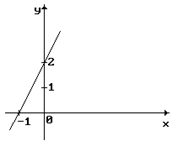
1.9.Определить угловой коэффициент k и величину отрезка b, отсекаемого прямой
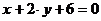
на оси OY.
1.10.Представлены уравнения прямых:
x+y+1=0, x+y=0, 2x+y+2=0 и y=2x.
Какие из заданных прямых параллельны?
1.11.Составить уравнение прямой, если известно, что прямая проходит через точку М(1;1) и имеет угловой коэффициент k=1.
Определить длину отрезка, заключенного между точками пересечения прямой
3у+4х-12=0
с осями координат.
1.12.Определить угол между прямыми
х -2у -2=0 и у= –2х+3.
Составить уравнение прямой, проходящей через точк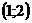и 
и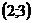 
.
1.13.Определить, с какими из прямых
у=3, у = х, х=5 и у=2х
пересекается окружность
х2 + у2 = 25.
1.14.Определить координаты центра и радиус окружности х2 +у2 –4х+8у–16=0.
1.15.Составить уравнение окружности, проходящей через точку М(-1;1) и центр которой находится в точке С(-4;5).
1.16.Определить координаты центра окружности, заданной уравнением
.
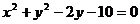1.17.Составить уравнение касательной к окружности
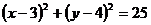
в точке (3;-1).
1.18.Составить каноническое уравнение окружности, представленной на рисунке.
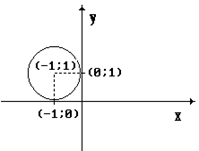
5.Кривые второго порядка.
1.19.Определить координаты фокусов эллипса
25x2+9y2 = 900.
1.20.Определить координаты фокуса и уравнение директрисы параболы
х2 =4у.
1.21.Определить, какая кривая определяется уравнением:
1.
.
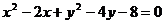2.
.
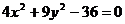3.
.
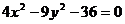4.
.
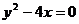6.Прямые, плоскости и сферы.
1.22.Определить, какое из уравнений:
2x-3y+z+1=0, x+2y-6=0 и x+3y=0
определяет плоскость, параллельную оси OZ.
1.23.Определить координаты нормального вектора к плоскости
2x-3y+z-6=0.
1.24.Определить взаимное расположение прямых
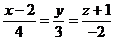и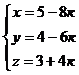
.
7.Поверхности второго порядка.
Определить, какая поверхность определяется уравнением
1.
.
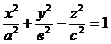2.
.
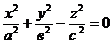3.
.
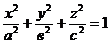8.Определители (детерминанты).
Вычислить определители:
1.
.
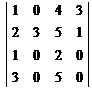2.
.
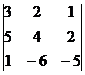3.
.
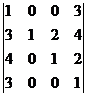Дата добавления: 2018-04-04; просмотров: 3729; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!