Мощность бесконечных множеств
В общем случае, справедливом и для бесконечных множеств, множества A и B является равномощных, или имеют одинаковую мощность, если можно установить взаимно однозначное соответствие между элементами этих множеств, т.е. если существует биекции f: A → B. Равномощных множества обозначаются как A ~ B.
Отношение ривнопотужности есть рефлексивным, симметричным и транзитивным, то есть отношением эквивалентности.
Для бесконечных множеств мощность множества может совпадать с мощностью ее собственной подмножества.
Примеры:
Множество натуральных чисел N равномощных множестве S = {1,4,9,16, ...}, состоящая из квадратов натуральных чисел. Необходима биекции устанавливается по закону (n, n 2), n ∈ N, n 2 ∈ S.
Множество Z всех целых чисел равномощных множестве P всех четных чисел. Здесь взаимно однозначное соответствие устанавливается следующим образом: (n, 2n), n ∈ Z, 2n ∈ P.
Числа алеф
Мощность множества натуральных чисел N обозначается символом 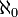 (Алеф-нуль). Последующие кардинальные числа в порядке возрастания обозначают
(Алеф-нуль). Последующие кардинальные числа в порядке возрастания обозначают 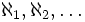 .
.
Зличеннисть и конечность множеств
Множество A называется счетное или счетное-бесконечной, если | A | ~ | N |. В этом случае говорят, что элементы такого множества можно занумеровать. Счетное есть множества целых Z, натуральных N и рациональных Q чисел.
Множество, есть конечная, или Счетное, называется не более чем счетное.
Бесконечная подмножество счетное множества является Счетное. Также бесконечное множество содержит счетное подмножество.
|
|
|
Для бесчисленных множеств, их мощность 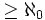 . То есть, Счетное множество в некотором смысле является "маленькой" из бесконечных множеств. Бесчисленными есть множества действительных R и комплексных C чисел.
. То есть, Счетное множество в некотором смысле является "маленькой" из бесконечных множеств. Бесчисленными есть множества действительных R и комплексных C чисел.
Мощность континуума
О множествах, равномощных множестве действительных чисел [или действительных чисел из интервала (0, 1)] говорят, что они имеют мощность континуума, и мощность таких множеств обозначается символом c. Континуум-гипотеза утверждает, что с = 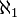 .
.
Свойства
- Две конечные множества равномощных тогда и только тогда, когда они состоят из одинакового числа элементов. То есть для конечного множества понятие мощности совпадает с привычным понятием количества.
- Для бесконечных множеств мощность может совпадать с мощностью своей собственной подмножества, например
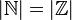 .
. - Более того, множество бесконечное тогда и только тогда, когда она содержит равномощных собственную (т.е. такую, которая не совпадает с основной множеством) подмножество.
- Теорема Кантора гарантирует существование мощной множества для любой данной: Множество всех подмножеств множества A имеет большую мощность, чем A, или
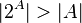 .
. - С помощью кантора квадрата можно доказать следующее полезное утверждение: Декартово произведение бесконечного множества A с самим собой равномощных A.
- Мощность декартова произведения:
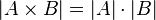
|
|
|
- Формула включения-выключения в простейшем виде:
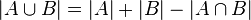
6.Числовые множества.Комплексные числа:
-натуральные, целые и рациональные числа;
-действительные числа;
-комплексные числа;
-алгебраические операции с комплексными числами;
-модуль и аргумент комплексного числа;
-геометрическое представление комплексных чисел;
-формула Эйлера;
-понятие о функции комплексного переменного.
Числовые множества. Множество комплексных чисел.
Дата добавления: 2018-04-04; просмотров: 2217; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
