I. Основные понятия и аксиомы теории множеств

Nbsp;   Дисциплина: Математика ( 1 часть из 2) Специальность (направление): все Форма обучения: все Форма контроля: зачет           Контрольные вопросы к экзамену ( зачету)                     ТЕОРЕТИЧЕСКАЯ ЧАСТЬ 1.Векторный анализ и аналитическая геометрия на плоскости: -системы координат на плоскости; -векторы и линейные операции над ними; -проекция вектора на ось; -разложение вектора на компоненты; -скалярное произведение векторов, его свойства, физический и геометрический смысл. -преобразование координат вектора при повороте системы координат. Основные задачи аналитической геометрии; -прямая линия на плоскости; -направляющий вектор; -общее уравнение прямой, различные формы уравнения прямой. Параллельность и перпендикулярность прямых; -уравнение окружности; -основные задачи на прямую и окружность; -кривые второго порядка: эллипс, гипербола, парабола. Канонические уравнения кривых второго порядка. 2.Векторный анализ и аналитическая геометрия в пространстве: -векторы в пространстве; -векторное произведение векторов, его свойства, физический и геометрический смысл; -смешанное произведение трех векторов, его свойства и геометрический смысл; -уравнение плоскости; -уравнение прямой в пространстве; -уравнение сферы; -основные задачи на плоскость, сферу и прямую в пространстве; -поверхности второго порядка. Канонические уравнения поверхностей второго по- рядка. 3.Матрицы и детерминанты: -обобщение понятия «вектор»; -векторы-столбцы и векторы-строки. Матрицы; -произведение строки на столбец; -произведение матрицы на столбец; -произведение матриц; -свойства линейных операций над матрицами; -определитель (детерминант) матрицы. Свойства детерминанта. Способы вычисле- ния детерминанта; -вычисление детерминанта раскрытием по строке (столбцу); -единичная матрица; -обратная матрица.Вычисление элементов обратной матрицы; -вырожденная матрица. Ранг матрицы.

Виды матриц.

· Матрица A размера m×n — это прямоугольная таблица чисел, расположенных в m строках и n столбцах

где a_ij (i =1, …, m; j =1, …, n) — это элементы матрицы A. Первый индекс i — это номер строки, второй индекс j — это номер столбца, на пересечении которых расположен элемент a_ij.
Сокращённое обозначение матрицы A=(a_ij)_m×n.

· Порядок матрицы — это число ее строк или столбцов.

· Главная диагональ квадратной матрицы — это диагональ, идущая из левого верхнего в правый нижний угол.

· Прямоугольная матрица — это матрица, у которой число строк не равно числу столбцов.

· Квадратная матрица — это матрица у которой число строк равно числу столбцов:

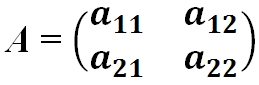
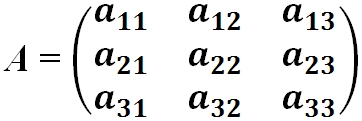
· Матрица-столбец — это матрица, у которой всего один столбец:

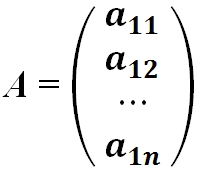
· Матрица-строка — это матрица, у которой всего одна строка:

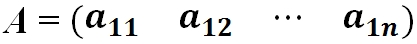
· Диагональная матрица — это квадратная матрица, у которой все элементы, кроме, быть может, стоящих на главной диагонали, равны нулю.

· Единичная матрица — это диагональная матрица, у которой все диагональные элементы равны единице:

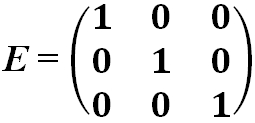
· Матрица квадратная диагональная:

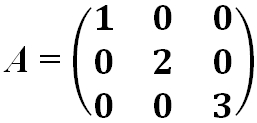
· Треугольная матрица — это квадратная матрица, у которой все элементы, расположенные по одну сторону главной диагонали, равны нулю.

· Матрица верхняя треугольная: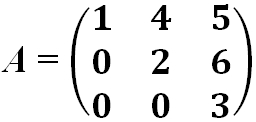

· Матрица нижняя треугольная:

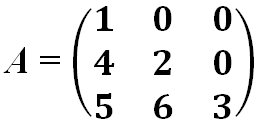
· Нулевая матрица — это матрица, все элементы которой равны 0:

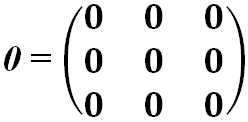
Операции над матрицами.

· Равенство матриц.
Две матрицы A (a_ij), B (b_ij) совпадают |A=B|, если совпадают их размеры и соответствующие элементы равны,
то есть при всех i, j a_ij=b_ij.

· Сложение матриц.
Суммой двух матриц A=(a_ij)_m×n и B=(b_ij) _m×n одинаковых размеров называется матрица C=(c_ij)_m×n=A+B тех же размеров, элементы которой определяются равенствами c_ij=a_ij+b_ij.

· Умножение матрицы на число.
Произведением матрицы A=(a_ij)_m×n на число λ ∈ R называется матрица B=(b_ij)_m×n=λA, элементы которой определяются равенствами b_ij=λa_ij. Пример 2.

· Умножение матриц.
Произведением матрицы A=(a_ij)_m×k на матрицу B=(b_ij)_k×n называется матрица C=(c_ij)_m×n=A· B размера m×n, элементы которой c_ij определяются равенством
c_ij=a_i1b_1j+a_i2b_2j+ … a_ikb_kj.
Таким образом, элемент матрицы C=A·B, расположенный в i-й строке и j-м столбце, равен сумме произведений элементов i-й строки матрицы A на соответствующие элементы j-го столбца матрицы B. Пример 3.

· Транспонированные матрицы.
Транспонированием матрицы А называется замена строк этой матрицы ее столбцами с сохранением их номеров.
Полученная матрица обозначается через A' или A^T. Пример 4.
Квадратная матрица называется симметричной, если A=A', то есть для элементов выполнены равенства a_ij=a_ji.

· Обратная матрица.
Квадратная матрица n–го порядка называется вырожденной, если определитель этой матрицы равен нулю, |A| = 0, и невырожденной, если |A| ≠ 0.
Матрица А^-1 называется обратной матрицей для некоторой квадратной матрицы А, если выполняется соотношение:

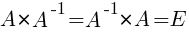
Если матрица А^-1 не вырождена, то существует, и притом единственная, обратная матрица А^-1, равная 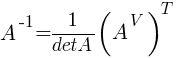, где А^V = A_ij — присоединенная матрица (матрица, составленная из алгебраических дополнений элементов исходной матрицы, стоящих на тех же местах).
1)
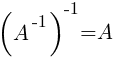
2)
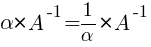
3)
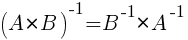
4)

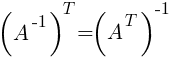
· Алгоритм нахождения А^-1 заключается в следующих пунктах:
1) Находим det A, проверяем det A ≠ 0.
2) Находим M_ij — все миноры матрицы A.
3) Определяем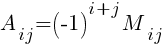
4) Строим матрицу алгебраических дополнений 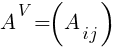и транспонируем: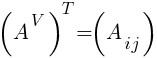
5) Делим каждый элемент матрицы на det A: 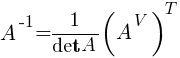Пример 5.

· Элементарные преобразования строк (столбцов) матрицы:
1) перестановка строк (столбцов);
2) умножение строки (столбца) на число α ≠ 0;
3) прибавление к элементам строки (столбца) матрицы элементов другой строки (столбца), умноженных на некоторое число.

· Решение матричных уравнений.
Матричное уравнение — это уравнение, содержащее неизвестную матрицу X и известные матрицы A, B, …, .
Простейшие типы матричных уравнений:
1) 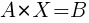. Матрица A – квадратная и невырожденная,
|A| ≠ 0, следовательно, существует обратная матрица A^-1.
Умножим уравнение на A^-1 слева: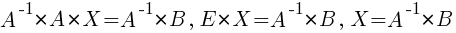
2) 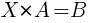. Матрица A – квадратная, |A| ≠ 0.
Умножим уравнение на A^-1 справа: .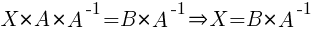
3) . Матрицы A и B – квадратные, |A| ≠ 0, |B| ≠ 0.
Умножим уравнение на A^-1 слева: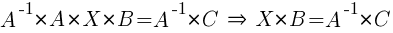
Умножим уравнение на B^-1 справа: .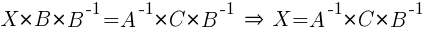

· Ранг матрицы.
Ранг матрицы A — это число, равное максимальному порядку отличных от нуля миноров.
M_k этой матрицы: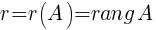
Матрицы называются эквивалентными, что обозначается
A ∼ B, если .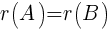
Ранг матрицы A вычисляется методом окаймляющих миноров или методом элементарных преобразований.

· Метод окаймляющих миноров.
Пусть в матрице A элемент a_ij ≠ 0, тогда M₁ ≠ 0 и r(A) ≥ 1. Окаймляем этот элемент элементами соседнего столбца и соседней строки (например, (j+1)–го столбца и (i+1)–й строки), получаем минор 2-го порядка: .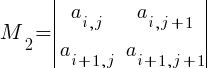
Если M₂, то присоединяем другие строки и столбцы, перебирая все возможные миноры 2-го порядка.
Если все миноры второго порядка равны нулю, то r(A) = 1; если же существует хотя бы один минор 2-го порядка, отличный от нуля, то r(A) ≥ 1.
Выбираем отличный от нуля минор 2-го порядка M₂ и окаймляем его элементами соседних строк и столбцов до минора 3-го порядка и так до тех пор, пока не будет выполнено условие: M_r ≠ 0, но все M_r+1 = 0. Пример 6.

· Метод элементарных преобразований.
Элементарные преобразования матрицы не меняют ее ранга.
К элементарным преобразованиям матрицы относятся следующие: транспонирование; перестановка строк (столбцов); умножение строки (столбца) на число α ≠ 0; прибавление к элементам строки (столбца) матрицы элементов другой строки, умноженных на некоторое число; отбрасывание нулевой строки (столбца) матрицы.
Для определения ранга матрицы A методом элементарных преобразований следует:
1) Переставить строки и столбцы так, чтобы в верхнем левом углу матрицы был ненулевой элемент.
2) Все элементы первого столбца, кроме a₁₁, обратить в ноль с помощью элементарных преобразований строк:

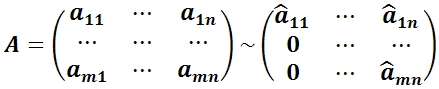
3) Переставить строки со 2–й по m и столбцы со 2–го по n так, чтобы a₂₂ ≠ 0. Повторить операцию (2) со вторым столбцом: во втором столбце все элементы, кроме a₁₂ и a₂₂, обратить в ноль.
Окончательно после многократного применения указанной процедуры и отбрасывания нулевых строк преобразованная матрица будет иметь вид:

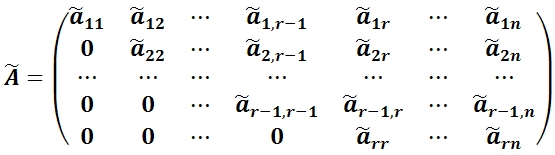
Тогда ранг матрицы A равен: rang A = rang Ã.

Определитель матрицы.

· Определитель квадратной матрицы.
Определитель первого порядка представляет собой число.
Определитель квадратной матрицы порядка n A=(a_ij)_m×n обозначается символами: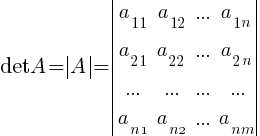
Определитель квадратной матрицы A второго порядка — это число, равное: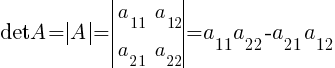
Определитель квадратной матрицы А третьего порядка — это число, равное:

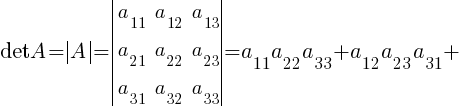
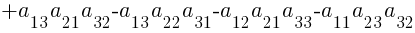. Пример 7.

· Правило треугольников (правило Саррюса):

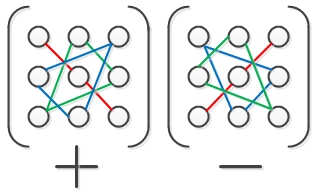
Знаки (+) и (–) соответствуют знакам определенных слагаемых, входящих в определитель, элементы определителя изображаются кружками, а соответствующие произведения — отрезками или треугольниками.

· Алгебраическое дополнение A=(a_ij) элемента a_ij — это определитель n-1 порядка, полученный из |A| вычеркиванием i-й строки и j-го столбца, на пересечении которых стоит элемент a_ij, взятый со знаком (-1)^i+j.

Свойства определителей.

1. Определитель квадратной матрицы А не меняется при транспонировании: |A^T|=|A|.

2. При перестановке местами любых двух строк (столбцов) определитель |A| меняет знак:

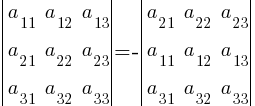
3. Определитель, содержащий две одинаковые строки (столбца), равен нулю.

4. Умножение всех элементов некоторой строки (столбца) определителя |A| на число k равносильно умножению определителя на это число:

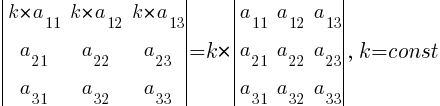
5. Если все элементы некоторой строки (столбца) определителя |A| равны нулю, то и сам определитель равен нулю (вытекает из предыдущего свойства при (k = 0):

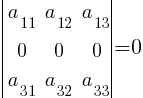
6. Если все элементы двух строк (столбцов) определителя |A| пропорциональны, то определитель равен нулю.

7. Если каждый элемент некоторой строки (столбца) определителя представляет собой сумму двух слагаемых, то такой определитель можно представить в виде суммы двух определителей:

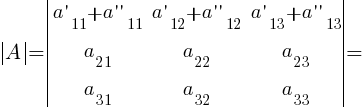
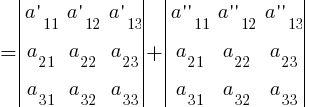
8. Если к элементам какой-нибудь строки (столбца) определителя |A| прибавить соответствующие элементы другой строки (столбца), умноженные на произвольный множитель k, то величина определителя не изменится:

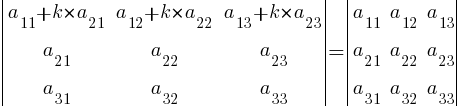
9. Определитель |A| численно равен сумме произведений элементов любой его строки (столбца) на соответствующие алгебраические дополнения:

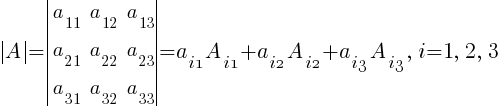
10. Определитель произведения матриц А и В равен произведению их определителей:
.

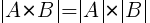Определителиn–го порядка.

· Минор М_ij или Δ_ij элемента а_ij ( иначе – дополнительный минор элемента а_ij) определителя n-го порядка — это определитель (n–1) порядка, полученный из исходного вычеркиванием i–й строки и j–го столбца, на пересечении которых стоит элемент a_ij.

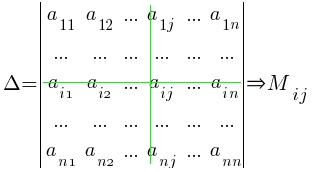
· Алгебраическое дополнение А_ij элемента а_ij — это его минор со знаком (-1)^i+j, где i – номер строки, а j – номер столбца, на пересечении которых стоит элемент a_ij, А_ij=(-1)^i+jM_ij или А_ij=(-1)^i+jΔ_ij. Пример 8.
Для определителей n-го порядка имеют место все перечисленные выше свойства определителей.

· Правило выбора знака перед минором в алгебраическом дополнении: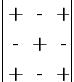

· Определитель n-го порядка |A| численно равен сумме произведений элементов любой его строки (столбца) на соответствующие алгебраические дополнения.

· Метод сведения к треугольному виду.
Используя свойства (1–9), определитель преобразуют к виду, когда элементы, лежащие по одну сторону от главной диагонали, становятся равными нулю. Преобразованный таким образом определитель равен произведению элементов, лежащих на главной диагонали.

 

4.Системы линейных алгебраических уравнений:

-связь матриц с системами линейных алгебраических уравнений (СЛАУ);

-матрица и расширенная матрица СЛАУ;

-вырожденные и невырожденные СЛАУ;

-теорема Кронекера-Капелли;

-решение невырожденной СЛАУ обращением матрицы;

-решение невырожденной СЛАУ методом Крамера;

-решение вырожденных СЛАУ;

-однородные СЛАУ. 

5.Элементы теории множеств:

-понятие множества;

-точечные и числовые множества;

-основные операции над множествами;

-декартово произведение множеств.

-соответствие между множествами;

-мощность множества.

Элементы теории множеств

I. Основные понятия и аксиомы теории множеств

За тысячи лет своего существования от простейших представлений о числе и фигуре математики пришла к образованию многих новых понятий и методов. Она превратилась в мощное средство изучения природы и гибкое орудие практики. XX век принес математике новые идеи, теории, расширилась сфера её применения. Математика занимает особое положение в системе наук – её нельзя отнести ни к гуманитарным, ни к естественным наукам. Но она ввела те основные понятия, которые используются в них. Таким понятием является понятие «множество», которое впервые возникло в математике и в настоящее время является общенаучным.

Первый набросок теории множеств принадлежит Бернарду Больцано («Парадоксы бесконечного», 1850). В этой работе рассматриваются произвольные (числовые) множества, и для их сравнения определено понятие взаимно-однозначного соответствия.

В конце 19 века Георг Кантор, немецкий математик, основоположник теории множеств, дал интуитивное определение понятию «множеству» так: «Множество есть многое, мыслимое как единое целое» [1]. Такое определение множества потребовало введения трех символов.

Первый из них должен представлять множество как нечто «единое», т.е. являться представителем самого множества. В качестве такого символа принято применять любую прописную букву какого-либо алфавита: например, обозначать множества прописными буквами латинского алфавита А, В, …, Х или какого-либо другого по соглашению.

Второй символ должен представлять «многое», то есть рассматриваться как элемент множества. В качестве этого символа принято использовать строчные буквы этого же алфавита: a, b, …, z.

Третий символ должен однозначно соотнести элемент множеству. В качестве соответствующего символа определен знак 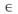, который происходит от первой буквы греческого слова (быть). Запись определяет отношение: х есть элемент Х. Для того чтобы указать, что х не есть элемент Х, пишут .

---

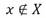Дата добавления: 2018-04-04; просмотров: 405; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!